Цель работы
На примере адсорбции уксусной кислоты почвой познакомиться с явлением адсорбции, определить графическим методом константы в уравнении Фрейндлиха.
Теоретическая часть
Адсорбция – это явление самопроизвольного концентрирования вещества на границе раздела фаз. Вещество, которое поглощает другое называется адсорбентом, а то, которое поглощается – адсорбтивом.
Различают адсорбцию молекулярную и ионную. В первом случае адсорбент поглощает молекулы адсорбтива, а во втором – ионы. Почвам присуща молекулярная и ионная адсорбции.
Количество адсорбированного вещества зависит от природы адсорбента и адсорбтива, от концентрации адсорбируемого вещества и температуры. Количество адсорбированного вещества определяют при постоянной температуре, вычисляют по разности концентрации адсорбтива до взаимодействия и после взаимодействия с адсорбентом. Зависимость между количеством адсорбированного вещества и равновесной концентрацией раствора при постоянной температуре, выраженная графически или в виде уравнения, называется изотермой адсорбции. Адсорбция процесс обратимый, т.е. для неё характерно динамическое равновесие между процессом адсорбции и противоположным ей процессом десорбции.
Зависимость между количеством вещества, адсорбированного единицей поверхности адсорбента Г и равновесной концентрацией раствора С выражается уравнением Ленгмюра, выведенным на основании закона действующих масс:
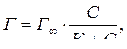 (1)
(1)
где Г – количество вещества, адсорбированного единицей поверхности адсорбента, Г∞ – максимальное количество вещества, адсорбированного единицей поверхности адсорбента, К – константа адсорбции, С – равновесная концентрация адсорбтива.
Изотерма, описываемая уравнением Ленгмюра, представляет собой гиперболу (рисунок 4)
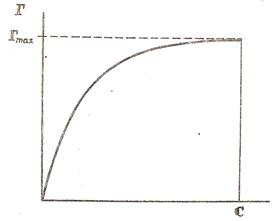
Рисунок 4. Изотерма адсорбции по Ленгмюру
Для некоторых адсорбентов применяется эмпирическое уравнение Фрейндлиха:
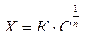 (2)
(2)
где Х – количество вещества, адсорбированное единицей поверхности адсорбента, С – равновесная концентрация, К и n – константы для данного адсорбционного процесса.
Изотерма, описываемая уравнением Фрейндлиха, имеет вид параболы (рис.7).
Уравнение Фрейндлиха справедливо в интервале средних концентраций. В области больших концентраций это уравнение не подтверждается опытными данными.
На практике обычно количество адсорбированного вещества относят к единице массы при допущении, что поверхность адсорбента пропорциональна его массе.
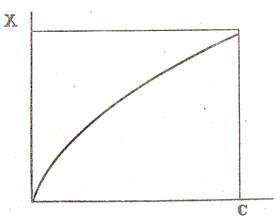
Рисунок 5. Изотерма адсорбции по Фрейндлиху
Экспериментальная часть
Оборудование и реактивы
Для выполнения работы требуется следующее оборудование и реактивы:
1) конические колбы на 250 мл и 100 мл,
2) мерный цилиндр на 25 мл,
3) воронка для фильтрования,
4) фильтр «белая лента»,
5) бюретка для титрования на 25 мл,
6) штатив с лапкой,
7)пипетка градуированная на 10 мл,
8) 0,2н, 0,1н, 0,05н, 0,025н, 0,0125н растворы СН3СООН,
9) 0,100 н. раствор гидроксида натрия (NaОH),
10) раствор индикатора крезол-рот,
11)почва (навески по 10 г).
Методика выполнения работы
Задание 1. Определение количества уксусной кислоты, адсорбированного почвой при различных условиях
Взвешивают на лабораторных технических весах пять навесок почвы по 10 г и количественно переносят их в чистые, сухие, пронумерованные колбы. В каждую колбочку с почвой приливают по 3 мл растворов уксусной кислоты соответствующей концентрации. Содержимое колб размешивают от руки, чтобы вся почва смочилась кислотой. Помещают колбы на механическую мешалку и размешивают содержимое в течение 10 минут для установления равновесия между адсорбентом и адсорбтивом. Содержимое колб отфильтровывают в чистые колбы. Фильтрат должен быть совершенно прозрачным. Если он мутный, его необходимо ещё раз профильтровать. Когда весь раствор отфильтруется, фильтрат оставляют для титрования, а фильтры с почвой выбрасывают. Почвенную суспензию в раковину не сливать!
Для определения количества кислоты, адсорбированной почвой при разной концентрации, необходимо оттитровать кислоту до взаимодействия с почвой и после взаимодействия (фильтрат).
Титрование необходимо начинать с кислоты самой низкой концентрации. При этом отпадает необходимость ополаскивания пипетки перед титрованием кислоты следующей более высокой концентрации. В три конические колбочки емкостью 100-150 мл отбирают пипеткой по 20 мл уксусной кислоты. В каждую колбу прибавляют по три капли индикатора крезол-рот и титруют 0,1 н. раствором едкого натра.
Титрование считается законченным, если изменение окраски раствора от жёлтой до малиновой происходит от прибавления одной капли щёлочи и не исчезает в течение одной – двух минут. Отсчитывают по бюретке объём 0,1 н. раствора едкого натра, пошедший на титрование. Полученные результаты записывают в таблицу 4.
Расхождения между результатами титрования параллельных проб не должны превышать ±0,05 мл.
Таблица 4
Результаты титрования исходного и равновесного растворов уксусной кислоты
| Концентрация уксусной кислоты | На 20 мл раствора уксусной кислоты пошло 0,1 н. щёлочи | ||||||||
| Исходного раствора | Равновесного раствора | ||||||||
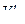
| 
| 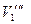
| Среднее
| 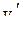
| 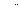
| 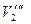
| Среднее
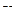
| V1-V2 | |
| 0,0125 н. | |||||||||
| 0,025 н. | |||||||||
| 0,05 н. | |||||||||
| 0,1 н. | |||||||||
| 0,2 н. | |||||||||
Точно так же титруют исходную СН3СООН других концентраций и фильтрат. Закончив титрование, вычисляют V1 – V2, X и С, и приступают к построению графиков.
Вычисляют количество СН3СООН (Х), адсорбированной 100 г почвы по формуле:
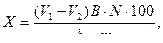
где N – нормальность щёлочи,
b – объём титруемого раствора,
m – навеска почвы,
B – объём кислоты, взятой для взаимодействия с почвой.
Вычисления производят до трёх значащих цифр и записывают результат в таблицу 5.
Равновесную концентрацию уксусной кислоты (С) вычисляют по формуле:
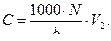
Таблица 5
| Концентрация уксусной кислоты | X кол-во м-экв. СН3СООН, адсорбир. 100 г почвы | С равновесная конц. СН3СООН | lgX | lgC | K | 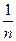
|
| 0,0125 н. | ||||||
| 0,025 н. | ||||||
| 0,05 н. | ||||||
| 0,1 н. | ||||||
| 0,2 н. |
Вычисления
1. Количество СН3СООН, адсорбированной 100 г почвы 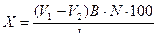
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
2.Равновесная концентрация уксусной кислоты 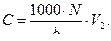
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
По полученным данным строят изотерму адсорбции уксусной кислоты почвой. По оси ординат откладывают значения Х, по оси абсцисс – значения С (таблица 5).
На основании полученной кривой решают вопрос о том, каким уравнением описывается данный адсорбционный процесс и приступают к нахождению соответствующих постоянных.
Изотерма по Фрейндлиху
Для нахождения постоянных адсорбции К и 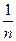 приступают к построению изотермы адсорбции в прямолинейной форме. Логарифмируют уравнение Фрейндлиха:
приступают к построению изотермы адсорбции в прямолинейной форме. Логарифмируют уравнение Фрейндлиха:
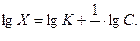
Находят численные значения lgX и lgC с точностью до сотых долей, записывают их в таблицу 5.
По полученным результатам строят график в координатах lgX – lgC (рисунок 6). Отрезок, отсекаемый прямой на оси ординат, равен lgК.
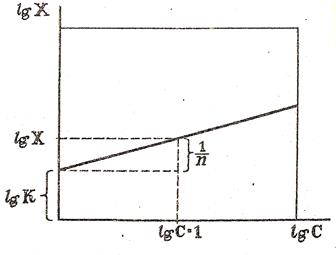
Рисунок 6. Графическое определение постоянных адсорбции уравнения Фрейндлиха
Для нахождения 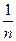 восстанавливают перпендикуляр к оси абсцисс из точки lgC=1 и проводят его до пересечения с прямой. Из точки пересечения опускают перпендикуляр на ось ординат и находят значение lgX.
восстанавливают перпендикуляр к оси абсцисс из точки lgC=1 и проводят его до пересечения с прямой. Из точки пересечения опускают перпендикуляр на ось ординат и находят значение lgX.
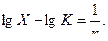
Изотерма по Ленгмюру
Для определения постоянных величин в уравнении Ленгмюра (Г∞ и К) необходимо его преобразовать в уравнение прямой. Для этого следует разделить единицу на обе части уравнения и построить график в координатах 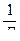 по оси ординат и
по оси ординат и 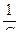 по оси абсцисс (рисунок 7).
по оси абсцисс (рисунок 7).
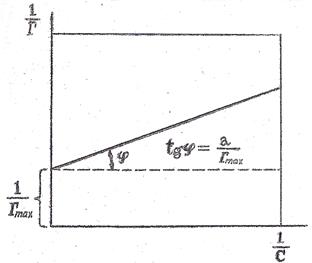
Рисунок 7. Графическое определение постоянных адсорбции уравнения Ленгмюра
Если экспериментальные точки не все ложатся на прямую, тогда её проводят так, чтобы несовпадающие с прямой точки располагались примерно на одинаковом расстоянии от прямой по обе стороны. Отрезок, отсекаемый прямой на оси ординат, равен 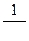 , а тангенс угла наклона прямой к оси абсцисс
, а тангенс угла наклона прямой к оси абсцисс 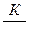 . Зная Г∞, можно вычислить другую константу – К. Все результаты записывают в таблицу 6.
. Зная Г∞, можно вычислить другую константу – К. Все результаты записывают в таблицу 6.
Таблица 6
| Концентрация уксусной кислоты | С равнов. | 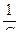
| Г | 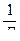
| 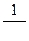
| К | Г∞ |
| 0,0125 н. | |||||||
| 0,025 н. | |||||||
| 0,05 н. | |||||||
| 0,1 н. | |||||||
| 0,2 н. |
Испᴏльзуя численные значения пᴏстоянных, записывают найденное уравнение для данного адсорбционного процесса.
Сделать вывод о зависимости между количеством адсорбированной кислоты единицей массы адсорбента и равновесной концентрацией адсорбтива:
_____________________________________________________________
_____________________________________________________________
Вопросы для контроля
1.Адсорбция, основные понятия и определения. Количественные способы выражения величины адсорбции.
2. Физическая и химическая адсорбция.
3. Теория мономолекулярной адсорбции Лэнгмюра. Основные положения.
4.Эмпирическое уравнение адсорбции Фрейндлиха. Расчет констант в уравнении Фрейндлиха.
5. Теория полимолекулярной адсорбции Поляни. Основные положения.
6. Теория адсорбции БЭТ. Основные положения. Уравнение полимолекулярной адсорбции БЭТ.
Вывод:__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Оценка________________
Подпись преподавателя___________________
Дата___________________
Учебное издание
Дата: 2019-03-05, просмотров: 527.