В открытом море наблюдатель видит вокруг судна водную поверхность, ограниченную малым кругом СС1 (рис. 5). Этот круг называется видимым горизонтом. Расстояние De от места судна М до линии видимого горизонта СС¹ называется дальностью видимого горизонта. Теоретическая дальность видимого горизонта Dt (отрезок АВ) всегда меньше его действительной дальности De. Это объясняется тем, что из-за различной плотности слоев атмосферы по высоте луч света распространяется в ней не прямолинейно, а по кривой АС. В результате наблюдатель может видеть дополнительно некоторую часть водной поверхности, расположенную за линией теоретического видимого горизонта и ограниченную малым кругом СС¹. Этот круг и является линией видимого горизонта наблюдателя. Явление преломления световых лучей в атмосфере называется земной рефракцией. Рефракция зависит от атмосферного давления, температуры и влажности воздуха. В одном и том же месте Земли рефракция может меняться даже на протяжении одних суток. Поэтому при расчетах берут среднее значение рефракции. Формула для определения дальности видимого горизонта:

• De = 2,08\Ге (3десь: De в морских милях; е - высота глаза наблюдателя над уровнем моря - в метрах).

В результате рефракции наблюдатель видит линию горизонта в направлении АС^ (рис. 5), касательном к дуге АС. Эта линия приподнята на угол г над прямым лучом АВ. Угол г также называется земной рефракцией. Угол d между плоскостью истинного горизонта НН/ и направлением на видимый горизонт называется наклонением видимого горизонта.

ДАЛЬНОСТЬ ВИДИМОСТИ ПРЕДМЕТОВ И ОГНЕЙ. Дальность видимого горизонта позволяет судить о видимости предметов, находящихся на уровне воды. Если предмет имеет определенную высоту h над уровнем моря, то наблюдатель может обнаружить его на расстоянии:

Дальность видимого горизонта. Таблица 22 МТ-75 :

Таблица вычислена по формуле:

Де =2.0809              ,

Входя в табл. 22 МТ-75 с высотой предмета h над уровнем моря, получают дальность видимости этого предмета с уровня моря. Если к полученной дальности прибавить дальность видимого горизонта, найденную в той же таблице по высоте глаза наблюдателя е над уровнем моря, то сумма этих дальностей составит дальность видимости предмета, без учета прозрачности атмосферы.

Для получения дальности радиолокационного горизонта Др принято выбранную из табл. 22 дальность видимого горизонта

увеличивать на 15%, тогда Др=2.3930                                                       . Эта формула

• Dn = Dh + De = 2,08\Ге + 2,08 \Г h (Здесь: Dn в морских милях, e - высота глаза наблюдателя над уровнем моря - в метрах, h - высота предмета над уровнем моря - в метрах).

На морских картах и в навигационных пособиях приводится заранее вычисленная дальность видимости огней маяков Dk с высоты глаза наблюдателя 5 м. С такой высоты De равна 4,7 мили. При е, отличной от 5 м, следует вносить поправку. Её величина равна:

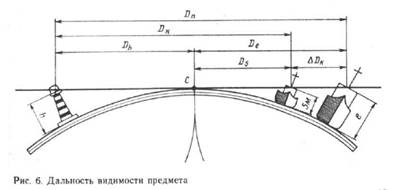• Л Dk = 2,08\Ге  - 4,7

Тогда дальность видимости маяка Dn равна:

• Dn = Dk + ΔDk (Здесь: Dn, Dk и Q Dk в морских миляк е - высота глаза наблюдателя над уровнем моря - в метрах).

Дальность видимости предметов, расчитанная по данной формуле, называется геометрической, или географической. Вычисленные результаты соответствуют некоторому среднему состоянию атмосферы в дневное время суток При мгле, дожде, снегопаде или туманной погоде видимость предметов, естественно, сокращается. Наоборот, при определенном состоянии атмосферы рефракция может быть очень большой, вследствие чего дальность видимости предметов оказывается значительно больше рассчитанной.

справедлива для стандартных условий атмосферы: давление 760 мм, температура +15°С, градиент температуры — 0.0065 градуса на метр, относительная влажность, постоянная с высотой, 60%. Любое отклонение от принятого стандартного состояния атмосферы обусловит частичное изменение дальности радиолокационного горизонта. Кроме того, эта дальность, т. е. расстояние, с которого могут быть видны отраженные сигналы на экране радиолокатора, в значительной степени зависит от индивидуальных особенностей радиолокатора и отражающих свойств объекта. По этим причинам пользоваться коэффициентом 1.15 и данными табл. 22 следует с осторожностью.

Сумма дальностей радиолокационного горизонта антенны Лд и наблюдаемого объекта высотой А представит собой максимальное расстояние, с которого может вернуться отраженный сигнал.

Пример 1.0пределить дальность обнаружения маяка высотой h=42 м от уровня моря с высоты глаза наблюдателя е=15.5 м. Решение. Из табл. 22 выбирают:

для h = 42 м.................. ДИ= 13.5 мили;

для е = 15.5 м......................... Де = 8.2 мили,

следовательно, дальность обнаружения маяка Дп = ДИ+Де = 21.7 мили.

Дальность видимости предмета можно определить также по номограмме, помещенной на вкладыше (приложение 6). МТ-75

Пример 2.Найти радиолокационную дальность объекта высотой h=122 м, если действующая высота радиолокационной антенны Нд = 18.3 м над уровнем моря.

Решение. Из табл. 22 выбирают дальности видимости объекта и антенны с уровня моря соответственно 23.0 и 8.9 мили. Суммируя эти дальности и умножая их на коэффициент 1.15, получают, что объект при стандартных условиях атмосферы, вероятно, будет обнаружен с расстояния 36.7 мили.

152. Визначення напрямів. Співвідношення між пеленгом, курсом та курсовим кутом.

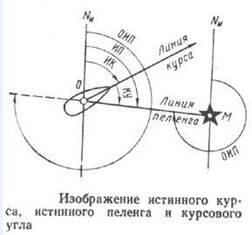
ИСТИННЫЕ КУРСЫ И ПЕЛЕНГИ. КУРСОВОЙ УГОЛ. Путевым углом называют двугранный угол между нордовой частью плоскости истинного меридиана и вертикальной плоскостью, совпадающей с линией перемещения судна. Если на судно не влияет ветер, вызывающий дрейф и течение, линия перемещения судна совпадает с направлением его диаметральной плоскости. В этом случае направление движения судна определяется истинным курсом. Истинным курсом (ИК) называется двугранный угол между нордовой частью плоскости истинного меридиана и носовой частью диаметральной плоскости судна. Направление на ориентир определяется двугранным углом между нордовой частью плоскости истинного меридиана и вертикальной плоскостью, проходящей через место наблюдателя и ориентир. Этот угол называется истинным пеленгом (ИП). Оба угла отсчитываются от нордовой части истинного меридиана по часовой стрелке от 0 до 360°. Угол, отличающийся от ИП на 180°, называется обратным истинным пеленгом (ОИП):

ОИП = ИП ± 180° или ИП = ОИП ± 180°

Знак “плюс” (+) при расчетах берется в том случае, если ИП (ОИП) меньше 180°, знак “минус” (-), если ИП (ОИП) больше 180°. ОИП является углом при ориентире, отсчитываемым от нордовой части истинного меридиана ориентира по часовой стрелке до направления с ориентира на судно (см. рис. 8). Курсовым углом (КУ) называется угол в плоскости истинного горизонта, заключенный между носовой частью диаметральной плоскости (ДП) судна и направлением на ориентир (см. рис. 8). Счет курсовых углов ведется по круговой системе от 0 до 360° по часовой стрелке или вправо и влево от ДП от 0 до 180°. Во втором случае КУ приписывают наименование правого (пр/б) или левого (л/б) борта. Между ИК, ИП и КУ, заданным по круговой системе счета, существует зависимость:

ИП = ИК + КУ ; ИК = ИП – КУ ; КУ = ИП – ИК.

Если КУ задан по полукруговому счету, то ИП и ИК вычисляют по формулам:

ИП = ИK + Kпр/б или ИП = ИК – Кл/б
ИК = ИП – Кпр/б или ИК = ИП + Кл/б

Когда КУ предмета равен 90° правого или левого борта, то говорят, что предмет находится на траверзе, указывая при этом наименование борта.