Этот этап направлен на построение математической модели исследуемого объекта. При выполнении полного факторного эксперимента он включает следующие операции:

· проверку однородности выборочных дисперсий;

· вычисление выборочных коэффициентов математической модели (уравнения регрессии);

· проверка статистической значимости выборочных коэффициентов математической модели;

· проверку адекватности математической модели.

Оценка дисперсии воспроизводимости (оценка ошибки опыта). Оценка дисперсии воспроизводимости опыта заключается в проверке того, что рассеяние результатов параметра y в каждой точке факторного пространства его исследования не превышает некоторой величины. Для этого вначале рассчитываются построчные дисперсии , и проверяется их однородность. Построчные дисперсии  находят по формуле

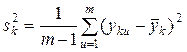,                                  (3)

где  - среднее арифметическое значение параметра y по результатам m параллельных опытов k-й строки матрицы планирования (k = 1, 2,…, N)

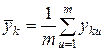;                                           (4)

u – номер параллельного опыта; y_ku – значение параметра в u – м параллельном опыте k – й строки матрицы.

В случае, когда число параллельных опытов во всех точках плана одинаково, проверку однородности дисперсий производят с помощью критерия Кохрена[19]. Он равен отношению максимальной построчной дисперсии 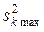 к сумме всех дисперсий по N строкам матрицы планирования

.

Если выполняется условие , т. е. расчетное значение критерия Кохрена G_р меньше теоретического G_т, то гипотеза об однородности дисперсий принимается. G_т находят по таблице математической статистики, например [1], для чисел степеней свободы f₁ = m-1 и f₂ = N и уровня значимости α. В технических расчетах обычно принимают α = 0,05. В случае не выполнения условия  принимают решение либо об увеличении числа параллельных опытов, либо об изменении метода измерения параметра y с целью увеличения точности его измерения.

При известных значениях построчных дисперсий дисперсия воспроизводимости опыта находится как средняя арифметическая 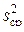 из построчных дисперсий  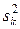всех N различных вариантов опытов

.                                         (5)

При этом ошибка опыта составит .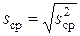

Вычисление выборочных коэффициентов математической модели (уравнения регрессии). Значения коэффициентов уравнения регрессии (3) вычисляются по формуле

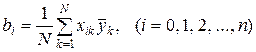,                           (6)

где i – номер коэффициента уравнения регрессии, в т. ч. свободного члена и коэффициентов при членах уравнения со смешанными произведениями факторов.

Оценка значимости коэффициентов уравнения регрессии. Для этого находят дисперсию коэффициентов уравнения регрессии по формуле

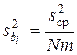                                           (7)

с числом степеней свободы f = N(m-1). Из формулы видно, что дисперсии всех коэффициентов одинаковые, т. к. они зависят только от ошибки опыта и числа опытов. Оценку значимости коэффициентов производят с помощью критерия Стьюдента 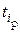, рассчитываемого по формуле

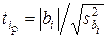                                             (8)

и проверки условия , где 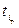 находят по таблице [1] для числа степеней свободы f = N(m-1) и уровня значимости α (обычно α = 0,05). Если данное условие выполняется, то i-й коэффициент признается значимым. Если для какого-то коэффициента условие  не выполняется, то соответствующий фактор признается незначимым, и его исключают из уравнения регрессии.

Оценка адекватности модели. Проверка гипотезы об адекватности полученной модели состоит в определении соотношения между дисперсией адекватности 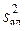 и дисперсией воспроизводимости  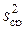(5). Дисперсия адекватности  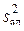является оценкой отклонения значения  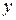параметра объекта, предсказанного уравнением регрессии (1), от результатов y эксперимента в различных точках факторного пространства. Ее при равном числе m параллельных опытов находят по формуле:

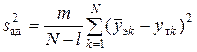,                                   (9)

в которой l – число членов в уравнении регрессии, оставшихся после оценки значимости коэффициентов; 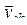 и 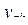 - опытные и теоретические (расчетные) значения параметра y в k – м опыте эксперимента.

Адекватность проверяют, оценивая отношение между дисперсиям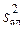и  и 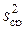, по критерию Фишера

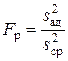                                              (10)

Критерий Фишера позволяет проверить нуль-гипотезу о равенстве двух генеральных дисперсий  и 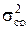. Если вычисленное по выборочным дисперсиям  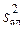и 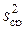 значение F_р критерия Фишера меньше его теоретического значения F_т для степеней свободы f_ад = N – l и f_ср = N(m-1) и заданного уровня значимости α, то нуль-гипотеза принимается. В противном случае гипотеза отвергается, и модель признается неадекватной объекту.

Проверка адекватности возможна только при f_ад > 0. Если число точек в плане эксперимента равно числу оцениваемых коэффициентов уравнения регрессии (N = l), то не остается степеней свободы (f_ад = 0) для проверки нуль-гипотезы об адекватности представления экспериментальных данных выбранной формой математической модели. В этом случае можно воспользоваться тем обстоятельством, что свободный член есть совместная оценка, т. е., например, в случае осуществления трехфакторного эксперимента 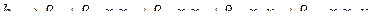. Если имеются повторные опыты в центре матрицы планирования, т. е. в точке (0, 0, 0,…, 0), то средний отклик дает несмещенную оценку 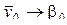. Поэтому, если разность  окажется статистически значимой ( 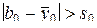), то это будет указывать на неадекватность линейной модели, т. е. на то, что все или часть коэффициентов β_ij, отражающих взаимодействие факторов, не равны нулю. Вместе с тем, если выбрана линейная математическая модель, то число членов проверяемой модели, как правило, меньше числа точек в плане и одна или несколько степеней свободы останутся для проверки гипотезы адекватности.

Контрольные вопросы по теме 4

1. Какими свойствами обладает план планируемого эксперимента, поясните эти свойства?

2. Для исследуемого параметра оптимизации принята линейная модель в виде полного степенного полинома

.

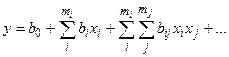Запишите его в развернутой форме для параметра y, который зависит от трех факторов. Что определяет выбор исходной (нулевой) точки в факторном пространстве планируемого эксперимента?

3. С какой целью осуществляют кодирование факторов? Какой эксперимент называют полным факторным экспериментом?

4. Приведите расширенную матрицу планирования ПФЭ 2².

5. Что понимают под рандомизацией последовательности опытов во времени?

6. В чем заключается оценка дисперсии воспроизводимости (оценка ошибки опыта)? Как рассчитать коэффициенты уравнения регрессии в относительных единицах по результатам полного факторного эксперимента?

7. Как рассчитать коэффициенты уравнения регрессии в натуральных единицах? Как оценить достоверность указанных коэффициентов? Как оценить адекватность уравнения регрессий?

[1] Метод от греческого слова methods – путь исследования, теория, учение.

[2] Индукция от лат. inductio – наведение.

[3] Дедукция, от лат. deductio –выведение.

[4] Аналогия, от rpеч. analogia - соответствие, сходство

[5] Абстракция, от лат. abstractio - отвлечение.

[6] Конкретное, от лат. concretus, буквально сryщенный, уплотненный, сросшийся.

[7] Ленин В. И. Философские тетради.

[8] Баклашов Н. И. и др. Натурный эксперимент: Информационное обеспечение экспериментальных исследований. - М., 1982; Капица. П. Л. Эксперимент, теория, практика. М., 1977; Налимов В. В. Теория эксперимента 1971; Тригг Дж. Решающий эксперимент в современной физике. М., 1974.

[9] Чернов А. П. Мысленный эксперимент. М., 1979.

[10] Митропольский А. К. Техника статистических вычислений. Изд. 2. М.: Наука, 1971. с.492.

[11] Маркова Е. В., Лисенков А. Н. Планирование эксперимента в условиях неопределенностей. М.: «Наука», 1973.

[12] Тюлин Н. И. Введение в метрологию. - М., 1970.

[13] Ветров А.А., Ломовацкий Г.И. Дисперсионный анализ в экономике. – М., «Статистика», 1975. 120 с.

[14] Налимов В. В., Голикова Т. И. Логические основания планирования эксперимента. – М.: Металлургия, 1981. – 128 с.

[15] Таблицы планов экспериментов для факторных и полиноминальных моделей. Справочное издание / Под ред. В. В. Налимова. М.: 1982

[16] Налимов В. В., Голикова Т. И. Логические основания планирования эксперимента. – М.: металлургия, 1981. – 128 с

[17] Митропольский А. К. Техника статистических вычислений. Изд. 2. М.: Наука, 1971. с.492.

[18] Маркова Е. В., Лисенков А. Н. Планирование эксперимента в условиях неопределенностей. М.: «Наука», 1973.

[19] Выбор критерия Кохрена вместо критерия Фишера обусловлен тем, что использование последнего при числе дисперсий более двух неэффективно, так как при проверке участвуют только наибольшая и наименьшая дисперсии.