Каждый фактор процесса имеет определенные границы изменения своей величины, внутри которых он может принимать или любое значение, или ряд дискретных значений. Например, такой фактор режима резания как подача является дискретным, в то время глубина резания может иметь любое из допустимых значение.
Совокупность всех значений, которые может принимать фактор, называется областью его определения. Совокупность всех значений, которую могут принимать все исследуемые факторы, составляют общую область определения факторов (область L на рис. 2).
 Заметим, что при решении задачи оптимизации область варьирования факторов (область M) должна составлять часть общей области определения факторов. Это обеспечивает более быстрый поиск точки оптимума. Кроме того, в области L может быть несколько точек оптимума. Поэтому на основе априорной информации устанавливаются ориентировочные значения факторов, комбинации которых дают наилучший результат. Этой комбинации (набору) значений факторов соответствует многомерная точка в факторном пространстве L, которая принимается за исходную точку при построении плана эксперимента. Значения факторов в исходной точке называются нулевыми уровнями.
Заметим, что при решении задачи оптимизации область варьирования факторов (область M) должна составлять часть общей области определения факторов. Это обеспечивает более быстрый поиск точки оптимума. Кроме того, в области L может быть несколько точек оптимума. Поэтому на основе априорной информации устанавливаются ориентировочные значения факторов, комбинации которых дают наилучший результат. Этой комбинации (набору) значений факторов соответствует многомерная точка в факторном пространстве L, которая принимается за исходную точку при построении плана эксперимента. Значения факторов в исходной точке называются нулевыми уровнями.
Выбор исходной (нулевой) точки весьма ответственное решение, поскольку от принятого выбора зависит количество экспериментов для решения поставленной задачи. Естественно, что чем выше уровень априорных сведений, чем опытнее экспериментатор, тем с большей вероятностью будет определено правильное положение нулевой точки в факторном пространстве.
Если же не имеется возможности хотя бы приблизительно указать положение нулевой точки, проводятся предварительные эксперименты по отысканию области оптимума (области M), центральную точку которой принимают в качестве нулевой точки.
Далее выбираются интервалы варьирования факторов. Интервал варьирования фактора – это такое значение фактора в натуральных единицах, прибавление которого к нулевому уровню дает верхний xiв, а вычитание – нижний уровень xiн фактора. Интервал варьирования i – го фактора обозначают через Δxi. Интервал (xiв - xiн) называется областью проведения эксперимента (область M).
Для упрощения записи условий эксперимента и обработки экспериментальных данных верхние и нижние уровни факторов принимают равными «+1», «-1», а нулевой – «0», что равносильно кодированию факторов по формуле
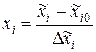 ,
,
 где
где 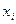 - кодированное значение фактора;
- кодированное значение фактора; 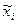 - значение фактора в именованных (натуральных) единицах;
- значение фактора в именованных (натуральных) единицах; 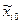 - значение основного (нулевого) уровня в именованных единицах;
- значение основного (нулевого) уровня в именованных единицах; 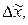 - интервал варьирования фактора (единица масштаба) в именованных единицах; i – номер фактора. Кодирование факторов, по сути, означает переход от системы координат в натуральных единицах (рис. 2) к системе координат в кодированной форме (рис.3). Каждая точка (+1, +1), (+1, -1), (-1, -1), (-1,+1) нового факторного пространства – это условия опыта в эксперименте.
- интервал варьирования фактора (единица масштаба) в именованных единицах; i – номер фактора. Кодирование факторов, по сути, означает переход от системы координат в натуральных единицах (рис. 2) к системе координат в кодированной форме (рис.3). Каждая точка (+1, +1), (+1, -1), (-1, -1), (-1,+1) нового факторного пространства – это условия опыта в эксперименте.
Выбор интервалов варьирования является неформализованным этапом планирования эксперимента и производится на основе имеющихся знаний об объекте, опыта и интуиции исследователя. При этом следует учитывать точность фиксирования факторов, силу влияния фактора на величину параметра объекта и величину ошибки измерения параметра. Все это поможет избежать ситуации, при которой интервал варьирования окажется недостаточным для того, чтобы уловить изменение параметра объекта.
Основное требование к интервалу варьирования заключается в том, чтобы он превышал удвоенную квадратическую ошибку фактора
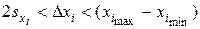 ,
,
где 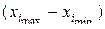 - область определения фактора.
- область определения фактора.
Минимально необходимое число уровней факторов определяется максимальным порядком интерполяционного полинома по данному фактору. Оно должно быть на единицу больше этого порядка.
Планирование эксперимента
Задачей планирования эксперимента является выбор числа и условий проведения опытов в эксперименте. Число опытов является важнейшей характеристикой плана эксперимента. В литературе[15] приведены структуры различных планов. Выбор плана во многом определяется целями и особенностями объекта исследования, в частности, уровнем знаний об объекте, видом принятой его математической модели, допустимой областью варьирования факторов и др. При выборе плана эксперимента учитываются также свойства планов: насыщенность, композиционность, рандомизированность, простота обработки результатов.
Насыщенность. Определяется числом опытов. Если число опытов равно числу неизвестных коэффициентов модели, то план является насыщенным, при меньшем числе опытов – ненасыщенным. Последний план не позволяет найти единственные оценки коэффициентов модели. Обычно выбирают планы с числом опытов N ≥ K + 1, где K – число неизвестных коэффициентов модели (без учета свободного члена в полиноминальной модели.
Композиционность. План считается композиционным, если при выборе модели более высокого порядка можно использовать все результаты опытов по плану меньшего порядка.
Рандомизированность. Это обеспечение случайного порядка проведения опытов для снижения влияния неконтролируемых факторов.
Простота обработки результатов. Многие планы допускают простую обработку результатов по простейшим формулам. Это свойство важно не только для ручной, но и для машинной обработки результатов.
| Таблица 1. Матрица планирования ПФЭ 22 | ||||
| № точки плана (опыта | x0 | Факторы | Параметр оптимизации y | |
| x1 | x2 | |||
| 1 | +1 | +1 | +1 | y1 |
| 2 | +1 | -1 | +1 | Y2 |
| 3 | +1 | +1 | -1 | y3 |
| 4 | +1 | -1 | -1 | y4 |
Выбор плана определяется видом принятой математической модели параметра исследуемого объекта. Например, если принята гипотеза о линейной зависимости параметра y от принятых двух факторов x1 и x2, то в плане эксперимента достаточно иметь два уровня для каждого фактора. Действительно, две точки дают возможность определить уравнение прямой линии. Используя кодированные значения факторов (+1, -1), условия эксперимента можно записать в виде таблицы, в которой строки отражают условия отдельных опытов, а столбцы – значения факторов (таблица 1). В таблицу помимо факторов вводится дополнительный столбец с фиктивной переменной x0, которой задают значение во всех строках +1. Этот столбец используется для определения свободного члена 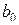 в уравнении регрессии
в уравнении регрессии
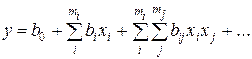 .
.
Столбцы x1 и x2 , содержащие сочетание уровней факторов, при которых следует проводить опыты, образуют матрицу плана. Поэтому таблицу 1, содержащую условия опытов, называют матрицей плана или матрицей планирования. Так в первой строке таблицы спланирован первый опыт, в котором факторам x1 и x2 придают максимальные значения; во второй строке – фактору x1 задают минимальное значение, а фактору x2 - максимальное и т. д.
Заметим, что матрица плана содержит все возможные комбинации уровней факторов. Число таких комбинаций N = 2k, где k – число факторов.
Эксперимент, в котором реализуются все возможные неповторяющиеся комбинации уровней независимых факторов, каждый из которых варьируется на двух уровнях, называется полным факторным экспериментом (ПФЭ 2k).
Полный факторный эксперимент позволяет получить опытные данные для построения полиноминальной линейной модели с членами, отражающими как влияние факторов на параметр объекта, так и влияние взаимодействия этих факторов. В частности, при исследовании объекта, состояние которого зависит от двух факторов и может быть описано уравнением регрессии
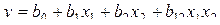 , (2)
, (2)
такой эксперимент позволяет найти все коэффициенты bi этой модели.
Матрица планирования с бόльшим числом факторов легко может быть построена, используя закономерности сочетаний значений факторов в их столбцах (таблица 2).
| Таблица 2. Матрица планирования ПФЭ от 22 до 24 | |||||||||
| № точки плана (опыта) | Тип эксперимента | Факторы | Параметр оптимизации y | ||||||
| x0 | x1 | x2 | x3 | x4 | |||||
| 1 | ПФЭ 24 | ПФЭ 23 | ПФЭ 22 | +1 | +1 | +1 | +1 | +1 | y1 |
| 2 | +1 | -1 | +1 | +1 | +1 | y2 | |||
| 3 | +1 | +1 | -1 | +1 | +1 | y3 | |||
| 4 | +1 | -1 | -1 | +1 | +1 | y4 | |||
| 5 |
| +1 | +1 | +1 | -1 | +1 | y5 | ||
| 6 | +1 | -1 | +1 | -1 | +1 | y6 | |||
| 7 | +1 | +1 | -1 | -1 | +1 | y7 | |||
| 8 | +1 | -1 | -1 | -1 | +1 | y8 | |||
| 9 |
| +1 | +1 | +1 | +1 | -1 | y9 | ||
| 10 | +1 | -1 | +1 | +1 | -1 | y10 | |||
| 11 | +1 | +1 | -1 | +1 | -1 | y11 | |||
| 12 | +1 | -1 | -1 | +1 | -1 | y12 | |||
| 13 | +1 | +1 | +1 | -1 | -1 | y13 | |||
| 14 | +1 | -1 | +1 | -1 | -1 | y14 | |||
| 15 | +1 | +1 | -1 | -1 | -1 | y15 | |||
| 16 | +1 | -1 | -1 | -1 | -1 | y16 | |||
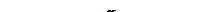
Геометрически матрица ПФЭ 23 представляет собой куб, координаты вершин которого отображают условия опытов, а центр куба является основным уровнем факторов (рис. 4). Длина ребер куба равна двум интервалам изменения факторов.
Для большего числа факторов k > 3 представить геометрически полный факторный эксперимент не представляется возможным. Но фигура, задающая область эксперимента в многомерном пространстве, является некоторым аналогом куба и называется гиперкубом.
В случае построения математической модели исследуемого объекта с учетом эффектов взаимодействия факторов составляется расширенная матрица планирования. В ней содержатся дополнительные столбцы с возможными комбинациями произведений факторов. В таблице 3 приведена расширенная матрица планирования полного факторного эксперимента 23.
| Таблица 3. Расширенная матрица планирования ПФЭ 23 | ||||||||||
| № точки плана | x0 | x1 | x2 | x3 | x1 x2 | x1 x3 | x2 x3 | x1 x2 x3 | Параметр оптимизации y | |
| 1 | + | + | + | + | + | + | + | + | y1 | |
| 2 | + | - | + | + | - | - | + | - | y2 | |
| 3 | + | + | - | + | - | + | - | - | y3 | |
| 4 | + | - | - | + | + | - | - | + | y4 | |
| 5 | + | + | + | - | + | - | - | - | y5 | |
| 6 | + | - | + | - | - | + | - | + | y6 | |
| 7 | + | + | - | - | - | - | + | + | y7 | |
| 8 | + | - | - | - | + | + | + | - | y8 | |
Свойства матрицы планирования. Рассмотренные матрицы планирования обладают свойствами, которые отражают их оптимальность с точки зрения построения по их результатам математической модели исследуемого объекта. В целом, различают две группы критериев оптимальности планов экспериментов, направленных на построение математических моделей в виде функций y = f(bij, xij)[16]:
· критерии, связанные с точностью оценок коэффициентов bij модели;
· критерии, связанные с ошибкой в оценке самой модели y.
К первой группе критериев относятся:
A – оптимальность (average variance – средняя дисперсия). Этот критерий требует, чтобы эллипсоид рассеяния оценок коэффициентов имел наименьшую сумму квадратов длин осей.
D – оптимальность (determinant - определитель). Для планов, удовлетворяющих этому критерию, эллипсоид рассеяния оценок коэффициентов модели имеет наименьший объем.
E – оптимальность (eigen value – собственное значение). Этот критерий гласит, что эллипсоид рассеяния оценок коэффициентов имеет наименьшую максимальную ось.
Ортогональность. Для ортогональных планов все оценки коэффициентов уравнения регрессии независимы, т. к. вектор столбцы плана линейно независимы (см. нижеприведенную формулу (1)); главные оси эллипсоида рассеяния оценок коэффициентов совпадают с направлением координатных осей в пространстве коэффициентов. Выполнение критерия ортогональности существенно упрощает вычисления.
Ко второй группе критериев относятся:
G – оптимальность (general variance – общая дисперсия). В соответствие с этим критерием максимальное значение дисперсии оценки модели минимально. Выполнение этого критерия позволяет не иметь точек со слишком низкой точностью оценки модели.
Q – оптимальность (qualitet - качество), согласно которому средняя дисперсия оценки модели минимальна.
Ротатабельность (rotation - вращение). Этот критерий требует такого расположения точек в области планирования, при котором ошибки оценки модели зависят только от расстояния до центра плана. Любое направление от центра плана равнозначно в смысле точности.
Униформность. В планах, отвечающих этому требованию, дисперсия оценки модели в некоторой области вокруг центра практически постоянна.
Приведенные матрицы соответствуют, по меньшей мере, двум критериям оптимальности: они удовлетворяют условиям ортогональности и ротатабельности, т. е. коэффициенты уравнения регрессии являются независимыми и точность предсказания значений параметра состояния объекта одинакова в любом направлении факторного пространства. Рассмотрим эти условия подробнее.
Прежде всего, заметим, что матрица планирования обладает свойством симметричности, согласно которому сумма k элементов любого i – го столбца равна нулю
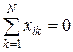 , (i=1, 2,…, n).
, (i=1, 2,…, n).
В этом легко убедиться из приведенных матриц планирования. Кроме того, матрица обладает свойством нормировки
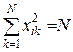 , (i=1, 2,…, n),
, (i=1, 2,…, n),
где n – число факторов; k номер точки плана.
Из таблицы 3 следует
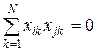 , (i, j = 1, 2,…, n, i ≠ j),
, (i, j = 1, 2,…, n, i ≠ j),
что указывает на выполнение условия ортогональности, являющимся одним из критериев, связанных с точностью оценок коэффициентов bij модели.
Критерий ротатабельности предполагает равенство и минимальность дисперсий предсказанных моделью параметра состояний исследуемого объекта для всех точек факторного пространства. Действительно, по закону накопления ошибок можно записать для дисперсии предсказанных уравнением регрессии значений параметра y
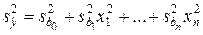 ,
,
где 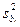 - дисперсия коэффициента модели bi.
- дисперсия коэффициента модели bi.
Из (1) следует, что дисперсии коэффициентов уравнения регрессии равны между собой. Тогда можно записать:
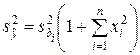
или с учетом того, что 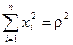 , где ρ радиус сферы
, где ρ радиус сферы
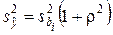 .
.
Отсюда следует, что дисперсия предсказанного значения параметра объекта зависит только от радиуса сферы, а следовательно не зависит от вращения координат в центре плана. Это является подтверждением свойства ротатабельности рассмотренных матриц планирования.
Осуществление эксперимента
Для удобства реализации опытов в матрице планирования все кодированные значения факторов заменяют их натуральными значениями. Такую матрицу планирования называют рабочей (таблица 4). В рабочую матрицу могут заносить также время проведения опытов, некоторые изменения в анализируемых пробах и другие сведения о проводимых опытах. Такая информация часто оказывается полезной в принятии решения о достоверности тех или иных опытах, о влиянии систематических ошибок т. п.
| Таблица 4. Рабочая матрица эксперимента исследования стойкости концевых фрез от геометрических параметров (заднего угла α, переднего угла γ и ширины ленточки f) | |||||
| Уровни факторов | Обозначение | αº | γº | f, мм | |
| 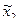
| 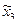
| |||
| Основной | 0 | 14 | 15 | 0,05 | |
| Интервал варьирования | 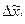
| 4 | 6 | 0,03 | |
| Верхний | +1 | 18 | 21 | 0.08 | |
| Нижний | -1 | 10 | 9 | 0,02 | |
Поскольку на изменение параметра объекта влияют помехи, обычно опыты плана реализуют несколько раз, получая m параллельных значений исследуемого параметра. Число m параллельных опытов назначают исходя из оценки достоверности результатов предварительного эксперимента. Обычно число параллельных опытов составляет 2 – 3, иногда 4 – 5. При этом стремятся эксперимент провести при равномерном дублировании опытов, т. е. каждая строка матрицы планировании имеет одинаковое число параллельных опытов (табл. 5).
В отдельных случаях эксперимент выполняется при неравномерном дублировании опытов, а иногда и без дублирования опытов. При равномерном дублировании опытов эксперимент обеспечивает повышенную точность, а математическая обработка полученных данных обладает простотой.
Чтобы избежать появления некоторой неслучайной связи между реализациями каждого опыта или серии опытов эксперимента производят рандомизацию последовательности опытов во времени, т. е. последовательность осуществления опытов назначают с использованием таблиц случайных чисел или иным способом генерирования случайных чисел.
| Таблица 5. Матрица планирования ПФЭ 23 с параллельными опытами | |||||||||
| № точки плана | x0 | Планирование | Параметр оптимизации y | ||||||
| x1 | x2 | x3 | yj1 | yj2 | … | yjm | 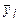
| ||
| 1 | + | + | + | + | y11 | y12 | + | y1m | 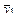
|
| 2 | + | - | + | + | y21 | y22 | + | y2m | 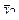
|
| 3 | + | + | - | + | y31 | y32 | - | y3m | 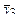
|
| 4 | + | - | - | + | y41 | y42 | - | y4m | 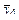
|
| 5 | + | + | + | - | y51 | y52 | - | y5m | 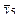
|
| 6 | + | - | + | - | y61 | y62 | - | y6m | 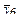
|
| 7 | + | + | - | - | y71 | y72 | + | y7m | 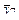
|
| 8 | + | - | - | - | y81 | y82 | + | y8m | 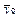
|
Рандомизация обычно проводится следующим образом. В таблице случайных чисел[17] из любого столбца выбирают числа в порядке их следования от 1 до N (количества точек плана). Если матрица планирования содержит параллельные опыты, то количество случайных чисел возрастает до mN, где m – число параллельных опытов. Каждое число от 1 до N или mN из таблицы случайных чисел берется только один раз.
Рандомизация опытов может осуществляться и другими способами[18].
Дата: 2019-02-19, просмотров: 722.