В научных исследованиях
Лк – 1,0 час. ПЗ – 1 час. СРС 4 час.
1. Понятия стохастических и корреляционных связей. Корреляционный анализ. Коэффициент корреляции и корреляционное отношение.
2. Регрессионный анализ. Задача регрессионного анализа. Методика регрессионного анализа.
3. Дисперсионный анализ. Сущность дисперсионного анализа. Применение дисперсионного анализа при исследовании степени влияния на параметр объекта факторов, определяющих его состояние или поведение.
Понятия стохастических и корреляционных связей. Корреляционный анализ. Коэффициент корреляции и корреляционное отношение
Понятия стохастических и корреляционных связей
Одной из основных задач экспериментальных исследований является задача нахождение связей между параметрами и факторами процессов и явлений, лежащих в основе их развития, и описание этих связей в математической форме. Из математического анализа известно, что если какая-либо физическая величина y определяется как однозначная функция одной или нескольких величин x1, x2,…, xn
y = f (x1, x2,…, xn),
то такая связь величины y с величинами x1, x2,…, xn является функциональной.
Функциональная связь может существовать и между случайными величинами. Но между случайными величинами, как правило, существует связь другого рода, которая проявляется в том, что одна из случайных величин реагирует на изменение другой изменениями своего закона распределения. Такая связь называется стохастической (вероятностной) или статистической. Эта связь обнаруживается при многократном проведении наблюдений (опытов), когда каждому заданному набору значений x1, x2,…, xn соответствует не одно определенное значение у, а целое распределение у (множество значений), которое изменяется с изменением x1, x2,…, xn. При наличии стохастической связи между двумя случайными величинами y и x изменение случайной величины y, соответствующее изменению величины x, раскладывается на две компоненты: собственно стохастическую, связанную зависимостью y от x, и случайную, обусловленную влиянием «собственных» случайных факторов величин y и x. Если первая компонента отсутствует, то величины y и x независимы. Если же стохастическая компонента не равна нулю, то между y и x есть стохастическая связь. Отсутствие второй компоненты указывает на то, что между величинами y и x имеется функциональная зависимость.
Среди стохастических связей наиболее простым ее видом и имеющим важное практическое значение является корреляционная связь.
Корреляционная связь между двумя случайными величинами выражается в том, что на изменение одной случайной величины другая случайная величина реагирует изменениями своего математического ожидания или среднего значения. То-есть понятие корреляционной связи является более узким, чем понятие стохастической связи, так как математическое ожидание является лишь одним из параметров распределения и еще не определяет закон распределения в целом. Корреляционная связь между случайными величинами может иметь форму линейной или нелинейной зависимости, например, в виде квадратичной параболы или гиперболы.
Корреляционный анализ
При исследовании стохастических связей возникают следующие вопросы:
1. Существует ли связь между случайными величинами y и x?
2. Какова сила этой связи?
3. Какую форму имеет связь, т. е. является она линейной или нелинейной (криволинейной)?
Эти вопросы рассматриваются теорией корреляции, являющейся одним из важных разделов математической статистики.
Пример 1.
Проведены испытания на стойкость 45-ти сверл диаметром 28 мм от величины заднего угла. Результаты испытаний приведены в таблице 1.
Следует установить наличие связи между стойкостью y и величиной заднего угла x, силу и форму этой связи.
Таблица 1. Результаты испытаний сверл на стойкость
| Задний угол x, град. | Стойкость y, мин | Количество сверл, шт. | 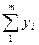
| 
|
| 6 | 127, 105 | 2 | 232 | 116 |
| 7 | 184, 175, 162, 428, 417 | 5 | 1366 | 273 |
| 8 | 39, 480, 392 | 3 | 911 | 304 |
| 9 | 615, 392, 1038, 435, 341, 417, 555, 300, 278, 289, 376, 337, 450, 525, 293, 310, 57, 122, 183, 183, 315, 149, 67, 136, 184, 180, 107, 201 | 30 | 8935 | 319 |
| 10 | 271 | 1 | 271 | 271 |
| 11 | 210, 223, 249, 188, 345, 315 | 6 | 1530 | 255 |
| 45 | 13245 | 294,33 |
Анализ результатов предварительно проведенной небольшой серии опытов позволил выдвинуть рабочую гипотезу о том, что связь между стойкостью y и величиной заднего угла x существует и является криволинейной.
Получить ответы на указанные выше вопросы и, следовательно, подтвердить или опровергнуть выдвинутую гипотезу можно с помощью таких статистических характеристик, как коэффициент корреляции и корреляционное отношение.
Коэффициент корреляции является показателем того, насколько связь между случайными величинами y и x близка к строгой линейной зависимости. С точки зрения наличия связи и формы связи коэффициент корреляции в одинаковой степени характеризует и слишком большую долю случайности, и слишком большую криволинейность имеющейся связи. Учитывая эти свойства коэффициента корреляции, определение связи между случайными величинами начинают с вычисления его значения, так как даже в случае криволинейной зависимости он характеризует степень приближения корреляционной зависимости к функциональной зависимости и дает ориентировочное представление о тесноте корреляционной связи. Поскольку в исследованиях имеют дело с данными выборки из генеральной совокупности, то вычисляют выборочный коэффициент корреляции r по формуле:
 , (1)
, (1)
где r – коэффициент корреляции величин x и y; xi и yi - измеренные значения случайных величин, например фактора x и параметра y изучаемого объекта; 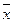 и
и 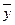 – средние арифметические значения величин x и y; n – число измерений (опытов).
– средние арифметические значения величин x и y; n – число измерений (опытов).
Значения r заключены между -1 и 1.
Расчет по данным табл. 1 коэффициента корреляции по формуле (1) дает следующий результат 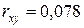 . Полученное значение коэффициента корреляции близко к нулю, что указывает на практическое отсутствие линейной связи между величинами x и y. Однако такое значение коэффициента корреляции не исключает наличие нелинейной связи между x и y, т. е. возможности принятия выдвинутой выше гипотезы.
. Полученное значение коэффициента корреляции близко к нулю, что указывает на практическое отсутствие линейной связи между величинами x и y. Однако такое значение коэффициента корреляции не исключает наличие нелинейной связи между x и y, т. е. возможности принятия выдвинутой выше гипотезы.
Нередко возникает вопрос, можно ли считать найденную величину выборочного коэффициента корреляции достаточной для статистически обоснованного вывода о наличии линейной корреляционной связи между исследуемыми переменными? Ответ на этот вопрос дает результат проверки значимости коэффициента корреляции, т. е. проверки нулевой гипотезы о том, что коэффициент корреляции не является статистически значимым (H0: ρ = 0, где ρ – коэффициент корреляции генеральной совокупности, из которой взята выборка). Эту проверку осуществляют при помощи критерия Стьюдента, расчетное (опытное) значение которого определяется по формуле
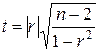 .
.
Критическое (теоретическое) значение критерия tкр находится из таблицы, в частности табл. 8 в приложении [4], по принятому значению доверительной вероятности P ( обычно 0,9; 0,95; 0,99) и числу степеней свободы k = n – 2. Если полученное значение t окажется больше, чем критическое tкр, то нулевую гипотезу следует отклонить и считать данное значение r значимым. Для рассматриваемого примера имеем:
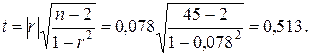
Критическое tкр для доверительной вероятности P = 0,95 и k = n - 2 = 43 по таблице приложения 2 составляет tкр = 2,02. Так как t < tкр, то гипотеза H0: r = 0 подтверждается, т.е. между величинами x и y нет линейной связи.
Коэффициент корреляции оценивает тесноту только линейной корреляционной связи. Оценка тесноты любой корреляционной связи осуществляется с помощью корреляционного отношения.
Выборочное корреляционное отношение – это отношение межгруппового среднего квадратического отклонения 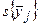 к общему среднему квадратическому отклонению
к общему среднему квадратическому отклонению 
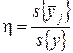 ,
,
где 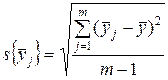 ;
; 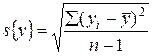 ,
,
в которых m – число выделенных групп результатов испытаний.
Значения η заключены между 0 и 1. В частности, для приведенных данных исследования зависимости между стойкостью y и величиной заднего угла x корреляционное отношение η=0,25.
Корреляционное отношение является мерой тесноты любой, в том числе и линейной, формы. Вместе с тем корреляционное отношение не позволяет судить, насколько близко расположены точки, найденные по данным наблюдений, к кривой определенного типа, например к параболе, гиперболе и т. д. Это объясняется тем, что при определении корреляционного отношения вид корреляционной зависимости между y и x во внимание не принимается.
Основные свойства коэффициента корреляции и корреляционного отношения [4].
а) Если коэффициент корреляции r = ±1, то y и x связаны линейной связью вида y = a + bx.
б) Если r = 0, то между y и x не может существовать прямолинейная связь, но криволинейная возможна.
в) Чем ближе значение r к ± 1, тем точнее и теснее корреляционная прямолинейная связь между y и x. Она ослабевает с приближением r к нулю.
г) Если корреляционное отношение η = 0, то между y и x нет корреляционной связи.
д) Если η = 1, то y связано с x однозначной (детерминированной) связью, т. е. всякому значению x соответствует одно определенное значение y.
е) Чем ближе η к единице, тем теснее связь y с x; чем ближе η к нулю, тем эта связь слабее.
В заключение отметим, что теория корреляции позволяет:
1. Установить форму корреляционной связи, т. е. вид корреляционной зависимости между y и x (линейная или нелинейная).
2. Оценить силу (тесноту) корреляционной связи. За критерий оценки принимается величина рассеяния значений y вокруг условного среднего 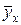 . Так, если при малом рассеянии мы имеем корреляционную связь значительной силы до предела, когда y и x связаны функционально, то при большом рассеянии зависимость y от x выражена слабо, вплоть до ее полного отсутствия вообще.
. Так, если при малом рассеянии мы имеем корреляционную связь значительной силы до предела, когда y и x связаны функционально, то при большом рассеянии зависимость y от x выражена слабо, вплоть до ее полного отсутствия вообще.
Понятие о множественной корреляции. Корреляционные связи могут существовать не только между двумя, но и между несколькими признаками. Например, овальность после чистового шлифования зависит от припуска на чистовое шлифование и от овальности после предварительного шлифования; припуск на зубошлифование зависит от величины деформации заготовки шестерни после термической обработки и от погрешностей, полученных после зубонарезания и т. п.
Исследование статистических связей между многими величинами составляет предмет теории множественной корреляции. В практике механической обработки деталей на станках чаще всего встречаются случаи линейной корреляционной связи между тремя величинами. Поэтому ограничимся рассмотрением простейшего случая линейной корреляционной связи между тремя величинами x, y и z, причем будем считать z величиной, зависящей от x и y. Линейная связь между z, x и y выражается уравнением
 , (2)
, (2)
где a, b и c – постоянные коэффициенты, которые вычисляются с помощью коэффициентов корреляции между x и y (rxy); x и z (rxz); y и z (ryz), а также средних квадратических отклонений σx, σy, σz по формулам:
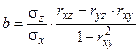 ; (3)
; (3)
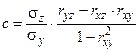 ; (4)
; (4)
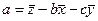 . (5)
. (5)
Мерой силы линейной связи между z и x, y в совокупности служит коэффициент множественной корреляции, который вычисляется по формуле
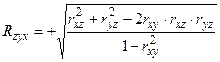 . (6)
. (6)
Коэффициент Rzyx всегда положительный и заключен между 0 и 1. если Rzyx = 0, то z не имеет линейной связи с x и y, но возможна криволинейная связь. Если Rzyx = 1, то между z, x и y, существует точная линейная связь вида 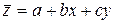 .
.
Для исследования наличия связей между x и z, y и z, а также оценки влияния x и y в отдельности на z пользуются частными коэффициентами, которые обозначаются через rxz(y) (между x и z при постоянном значении y) и ryz(x) (между y и z при постоянном значении x).
Эти коэффициенты вычисляются по формулам:
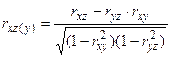 ; (7)
; (7)
 , (8)
, (8)
где rxy, rxz, ryz – парные коэффициенты корреляции.
Корень в знаменателе формул (7) и (8) всегда берется со знаком плюс. Смысл частных коэффициентов заключается в том, что они служат мерой линейной связи между x и z при постоянном значении y, а также между y и z при постоянном значении x. Значения коэффициентов заключены между -1 и +1. Когда они равны 0, частная связь между x и z, y и z не может быть линейной; если равны ±1, то связь линейная. Чем ближе значения частных коэффициентов к ±1, тем теснее связь, тем ближе она к линейной связи.
Сравнивая значения rxz(y) и ryz(x), можно установить, какой из факторов x или y оказывает более сильное влияние на z. Чем большее влияние частного коэффициента корреляции, тем теснее связь данного фактора с z и тем сильнее его влияние на z. Для определения коэффициентов корреляции rxy, rxz, ryz составляют корреляционные таблицы для x и y, x и z, y и z и производят необходимые вычисления, аналогичные с вычислениями при исследовании парных корреляций.
Пример 2. Кольца подшипников подвергаются предварительному и окончательному шлифованию на двух бесцентровошлифовальных станках. Статистическими исследованиями установлено, что овальность x после предварительного шлифования, припуск y под окончательное шлифование и овальность z после окончательного шлифования характеризуются показателями:
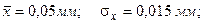
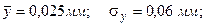

Кроме того, установлены следующие величины коэффициентов корреляции между x, y, и z:
rxy = 0,5; rzx = 0,6; rzy = 0,4.
Необходимо определить коэффициент множественной корреляции Rzyx, уравнение регрессии z на x и y и частные коэффициенты корреляции.
По формулам (3)-(5) найдем значения коэффициентов a, b и c:
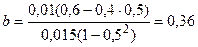 ;
;  ;
;
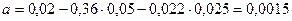 .
.
Уравнение корреляционной связи z с x и y имеет вид
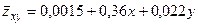 .
.
Вычислим частные коэффициенты корреляции:
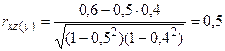 ;
; 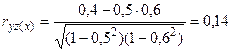 .
.
Коэффициент множественной корреляции равен
 .
.
Этот коэффициент достаточно велик и свидетельствует о наличии линейной связи между z и x, y. Частные коэффициенты корреляции показывают, что влияние x на z сильнее влияния y, так как связь между x и z теснее, чем связь между y и z. То же вытекает из анализа уравнения регрессии z на x и y. С увеличением y в два раза при x =const z увеличится на 5,75%; с увеличением x в два раза при y =const z увеличится на 94%. Следовательно, влияние овальности колец после предварительного шлифования сильнее, чем влияние припуска под чистовое шлифование на величину овальности колец после окончательной их обработки.
Дата: 2019-02-19, просмотров: 392.