Корреляционный анализ позволяет установить отсутствие или наличие связи между факторами и исследуемым параметром объекта, силу и форму этой связи. Однако остается не выясненным вопрос, какой математической зависимостью может быть описана эта корреляционная связь. Ответ на этот вопрос дает регрессионный анализ.
Задачей регрессионного анализа является установление вида эмпирических зависимостей, отражающих связи между характеристиками изучаемого объекта, и оценку адекватности построенных зависимостей. При наличии корреляционной зависимости между y и x в виде уравнения
y = f (x)
его принято в регрессионном анализе называть уравнением регрессии y на x, функцию f (x) – регрессией y на x.
Различают однофакторную и многофакторную регрессионные зависимости. Однофакторная регрессия может быть аппроксимирована прямой линией, параболой, гиперболой, показательной функцией, полиномом и др. Если параметр y является функцией от нескольких факторов, ее графическое представление будет иметь вид n‑мерной поверхности.
Проведение регрессионного анализа рассмотрим на примере однофакторного регрессионного анализа. Такой анализ имеет широкое практическое применение в технологии машиностроения. В частности, он используется при исследовании зависимости жесткости узлов станка от нагрузки, исследовании зависимостей высоты шероховатостей обработанной поверхности от какого-либо фактора режима резания, стойкости режущего инструмента, устойчивости технологического процесса во времени и т. д.
Методика однофакторного регрессионного анализа включает в себя выполнение следующих процедур.
1) Построение корреляционного поля. Эта процедура сводится к нанесению в плоскости XY точек результатов эксперимента.
2) Проведение визуального анализа полученного поля. По тесноте и характеру расположения точек можно ориентировочно судить о виде регрессионной зависимости между параметром y и его фактором x.
В случае большого объема экспериментальных данных вместо корреляционного поля строится эмпирическая линия регрессии. Для этого диапазон изменения фактора x разбивается на произвольное число равных интервалов. Для каждого интервала определяется среднее значение исследуемого параметра y
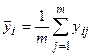, i = 1, 2, …, n,
где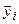 
- среднее арифметическое значение параметра y в i – й группе;
yij – j‑е значение параметра y в i – й группе; n – число групп, m – число значений параметра y в i – й группе.
Далее на плоскости XY наносят точки средних значений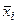 
, 
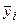(i = 1, 2,…, n) и соединяют их отрезками прямых линий. Полученная ломаная линия является эмпирической линией регрессии. Ее вид позволяет принять решение о виде теоретической регрессионной зависимости между параметром y и его фактором x.
3) Аппроксимация в соответствии с видом эмпирической линии регрессии ее теоретической регрессионной зависимостью, например,
линейной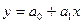 
;
параболой второго порядка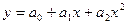 
;
параболой третьего порядка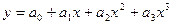 
;
гиперболой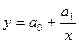 
и др.
4) Определение неизвестных коэффициентов ai выбранной регрессионной зависимости. Обычно определение коэффициентов регрессионной зависимости осуществляют методом наименьших квадратов, согласно которому сумма квадратов отклонений теоретических значений исследуемого параметра от экспериментальных должна быть минимальной.
5) Проверка адекватности теоретической регрессионной зависимости. Она в зависимости от условий (малый или большой объем выборки и др.) может осуществляться с использованием критериев Фишера (для малых выборок), Пирсона, Романовского и др.
Сущность проверки на адекватность заключается в сопоставлении результатов расчета по полученной теоретической модели (регрессионной зависимости) исследуемого параметра объекта с экспериментальными данными. Для этого рассчитывается экспериментальное (опытное) значение критерия, например, Фишера kэ и сравнивается с его теоретическим (табличным) kт, выбираемым при требуемой доверительной вероятности p ( обычно p = 0,95). Если kэ< kт – модель адекватна, в противном случае – модель неадекватна.
Опытное значение критерия Фишера kэ вычисляется по формуле
,
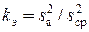где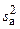 
– дисперсия адекватности; 
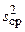– средняя дисперсия всех результатов эксперимента. Эти дисперсии определяются по формулам [3]:
; 
,
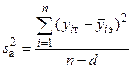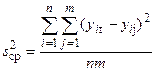в которых yiТ, yiэ – теоретические и опытные значения параметра y в i - й группе;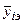 
, - опытное среднее арифметическое значение параметра y в i - й группе;
d – число коэффициентов теоретического уравнения регрессии.
Значение kт принимается из таблицы, приводимой во многих литературных источниках по математической статистике. Входными данными для выбора теоретического значения критерия Фишера являются уровень доверительной вероятности p и числа f1, f2 степеней свободы, определяемые как f1 = n-d и f2= n(m-1).
Дисперсионный анализ.
Выше рассмотрена возможность решения задачи о наличии и тесноте связей между факторами и исследуемым параметром объекта с помощью коэффициента корреляции и корреляционного отношения. Однако во многих случаях для решения этой задачи удобнее применять дисперсионный анализ. Различают однофакторный и многофакторный дисперсионный анализ.
Независимо от вида дисперсионного анализа, его сущность заключается в разложении общей дисперсии параметра на отдельные составляющие, обусловленные действием отдельных факторов и их взаимодействий, а также действием случайных причин и оценке существенности влияния на параметр каждого из факторов.
Рассмотрим применение дисперсионного анализа при исследовании влияния на параметр объекта одного фактора.
Имеется единичный фактор x, который принимает p различных уровней (значений). Пусть на каждом уровне сделано n наблюдений, так что общее число наблюдений N = np. Все результаты наблюдений представлены в виде множества значений yij (i =1, 2,…, p; j =1, 2,…, n). Требуется определить влияние фактора x на параметр y и достоверность этого влияния.
Обозначим через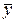 
среднее значение всей совокупности наблюдений, через 
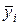- среднее значение результатов наблюдений на i-м уровне фактора. Их значения определяются по формулам
; 
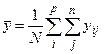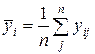, i = 1, 2, …, p.
Является очевидным, что общее отклонение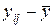 
отдельного результата yij от общей средней 
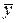равна сумме отклонения 
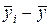среднего результата 
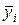наблюдений на i-м уровне фактора x от общей средней 
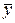и отклонения 
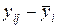внутри уровня, т. е. 
.
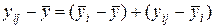Возведем обе части уравнения в квадрат и, суммируя по i и j, получим
.
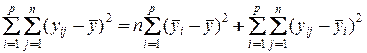Член с перекрестным произведением исчезает, так как сумма отклонений любой группы наблюдений от их среднего значения равна нулю.
Заметим, что левая часть полученного уравнения есть сумма квадратов отклонений результатов наблюдений от общей средней. Обозначим эту сумму через w.
Первое слагаемое правой части уравнения является суммой квадратов отклонений средних результатов на уровнях фактора от общей средней - w1, т. е. эти отклонения обусловлены влиянием фактора x. Второе слагаемое уравнения есть сумма квадратов отклонений внутри уровня ‑w2. Эти отклонения вызваны влиянием случайных причин. Таким образом, имеем
.
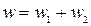Число степеней свободы вариации представляет собой число независимых отклонений индивидуальных значений параметра от его среднего значения. Так, если есть N наблюдений и определена средняя совокупности, то число независимых отклонений от средней будет N -1; последнее отклонение выражается через все предыдущие. Таким образом, w имеет N -1 степеней свободы, w2 имеет N – p степеней свободы, так как w2 вычисляется по отклонениям N наблюдений от p выборочных средних, т. е. N – p независимых параметров
N – p = np - p = p(n – 1).
Аналогично w, w1 имеет p –1 степеней свободы, так как w1 вычисляется, исходя из отклонений p средних для независимых уровней фактора x от общего среднего.
Таким образом, величины
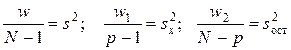
являются соответственно общей дисперсией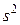 
, дисперсией 
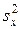, характеризующей влияние на параметр y фактора x и остаточной дисперсией 
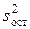, обусловленной влиянием на параметр y случайных причин.
Оценка степени влияния фактора на параметр объекта осуществляется с помощью критерия F Фишера (используют также и критерий R Романовского). Критерий Фишера является отношением дисперсии, обусловленной влиянием фактора, к дисперсии, вызванной действием случайных причин (остаточной дисперсии)
.
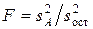Задавшись доверительной вероятностью (или уровнем надежности) и имея степени свободы критерия (числа в знаменателях для s2: f1= p -1, f2= N -p), находят табличное Fтабл значение критерия. Если F > Fтабл, то с заданным уровнем надежности можно заключить, что влияние фактора на изменчивость параметра объекта существенно.
Сущность двухфакторного дисперсионного анализа практически не отличается от однофакторного анализа. В данном случае осуществляется выделение из общей дисперсии составляющих, характеризующих влияние каждого фактора в отдельности, влияние на параметр совместного действия этих факторов и влияние случайных причин.
Методика выделения составляющих зависит от разновидности двухфакторного дисперсионного анализа[13]. Прежде всего, различают две модели: модель I и модель II. Модель I предполагает факторы с фиксированными уровнями. В модели II оба фактора характеризуются случайными уровнями. Если один фактор имеет фиксированные, а другой – случайные уровни, то такую модель называют смешанной. Кроме того, выделяют две классификации: многостороннюю и иерархическую. В первой оба фактора оказывают одинаково главное влияние. Во второй один из факторов таков, что ему нельзя приписать главное влияние, он как бы «сгруппирован» внутри главного фактора. И еще одно обстоятельство, которое приходится учитывать при проведении двухфакторного дисперсионного анализа. Оба фактора могут иметь как одинаковое число уровней своего изменения, так и разное. Все приведенные условия предопределяют различную методику вычисления составляющие дисперсии.
Контрольные вопросы по теме 3
1. В чем отличие стохастической связи между случайными величинами от функциональной связи между величинами?
2. Корреляционная и стохастическая связи между случайными величинами. Что объединяет и что различает эти связи?
3. Какие три вопроса исследуют с помощью корреляционного анализа?
4. Что характеризует коэффициент корреляции? Какие значения он может принимать?
5. Что оценивает корреляционное отношение? Какие значения может принимать корреляционное отношение?
6. Какую задачу решают с помощью регрессионного анализа? Какие процедуры включает в себя регрессионный анализ?
7. Как проверяется адекватность полученной регрессионной зависимости?
8. В чем заключается сущность дисперсионного анализа?
9. Как вычисляются общая дисперсия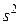 
, дисперсия 
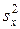, характеризующая влияние на параметр y фактора x и остаточная дисперсия 
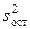, обусловленная влиянием на параметр y случайных причин?
10. Что характеризует критерий Фишера при осуществлении дисперсионного анализа?
11. В каком случае гипотеза о влиянии фактора на параметр исследуемого объекта считается не состоятельной?
Тема 4. Планирование эксперимента
Л – 1,0 час. ПЗ – 2 час. СРС 4 час.
1. Элементы теории планирования эксперимента.
2. Методика планирования экстремального полного факторного эксперимента
3. Обработка результатов полного факторного эксперимента.
Литература.
1. Кане М. М. Основы научных исследований в технологии машиностроения: Учеб. пособие для вузов. – Мн.: Выш. шк., 1987.
2. Основы научных исследований: Учебник для вузов / под ред. В. Г. Кучерова / ВолгГТУ. Волгоград, 2004.
3. Пойлов В. З. Основы научных и инженерных исследований: учеб. пособие / В.З. Пойлов. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008.
4. Спиридонов А. А. Планирование эксперимента при исследовании технологических процессов. М.: Машиностроение, 1981. – 184 с.
1. Элементы теории планирования эксперимента
Планирование эксперимента применяется для решения широкого круга задач: построения эмпирических моделей, изучения кинетики и механизма явлений и процессов, оптимизации процессов и др. Наибольшее значение для практики имеет оптимизация процессов (планирование экстремальных экспериментов).
Возникновение современных статистических методов планирования экспериментов связано с именем Р. А. Фишера. Первая работа в области планирования экстремальных экспериментов была опубликована в 1951 г. Боксом и Уилсоном в Англии. Идея метода Бокса-Уилсона весьма проста. Экспериментатор ставит последовательно небольшие серии опытов, в каждом из них одновременно варьируются по определенным правилам все факторы. Серии организуются таким образом, чтобы после математической обработки предыдущей серии можно было выбрать условия проведения (т. е. спланировать) следующую серию. Так последовательно, шаг за шагом, достигается область оптимума. Важным достоинством метода является его универсальность, пригодность в подавляющем большинстве исследований.
В нашей стране теория планирования экспериментов получило свое развитие с 1960 г. под руководством В.В. Налимова. Планирование эксперимента, как и вся математическая теория эксперимента, развивается в основном как раздел прикладной математики.
Теория планирования эксперимента[14] определяет условия оптимального проведения исследования, в том числе и при неполном знании физической сущности явления. Это обеспечивается рядом концепций, составляющих основу этой теории. К ним относятся концепция математического моделирования, концепция варьирования всех факторов объекта по определенному плану, концепция последовательного эксперимента, рандомизации, оптимального использования факторного пространства и др. Все это позволяет исследовать и оптимизировать сложные системы и процессы, достигать высокую эффективность самого эксперимента и точность определения исследуемых параметров.
Независимо от поставленных задач исследования методика планирования эксперимента является общей и включает в себя следующие этапы:
- выбор математической модели объекта;
- выбор факторов, определяющих состояние и поведение объекта исследования;
- определение области экспериментирования, основного уровня факторов и интервала их варьирования;
- планирование эксперимента;
- осуществление эксперимента;
- обработка результатов эксперимента.
Рассмотрим основные положения методики планирования экстремального полного факторного эксперимента.
2. Методика планирования экстремального
Дата: 2019-02-19, просмотров: 435.
