Рассмотренная выше основная процедура достаточна для сравнения КС о . Но при сравнении КС а возникает дополнительная проблема.
Получение корректных результатов в процессе попарного сравнения альтернатив и выявления предпочтений ЛПР связано с известным предположением о независимости критериев по предпочтению. В большинстве реальных приложений это предположение выполняется в результате разумного выбора набора независимых критериев. Однако избежать завуалированных связей между критериями не всегда удается. Указанием на возможное присутствие таких связей может служить повышенная частота ошибок ЛПР при определении предпочтений, приводящая к нетранзитивности результатов.
Для проверки условия независимости по предпочтению предлагается дополнительная процедура.
Сформулируем условие независимости при сравнении двух КС а по их ценности для ЛПР. Критериальные соответствия независимы, если результат сравнения ценностей векторов с двумя ненулевыми значениями компонентов 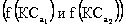 не зависит от одинаковых значений других компонентов, т. е. если не найдется какого-либо третьего КС а с
не зависит от одинаковых значений других компонентов, т. е. если не найдется какого-либо третьего КС а с  при котором результат сравнения может быть иным.
при котором результат сравнения может быть иным.
Заметим, что данное условие, в отличие от общепринятого условия независимости по предпочтению, сформулировано относительно троек КС а . Обоснованием этого подхода служат исследования, показывающие, что зависимость критериев обычно проявляется как зависимость результатов сравнения оценок двух критериев от оценок по третьему критерию. Именно такая форма зависимости отмечалась в [10, 11 ]. Появление более сложной групповой зависимости неопределенно по своей природе и трудно обнаружимо. Этот факт позволяет утверждать, что если нет троек зависимых КС а , условие независимости при сравнении альтернатив не нарушается при любом количестве одинаковых компонентов вектора соответствия.
Чтобы проверить выполнение условия независимости, необходимо получить дополнительную информацию от ЛПР. Когда выполняется дополнительная процедура, вопросы, задаваемые ЛПР (см. основную процедуру), повторяются при следующем дополнительном условии: «по третьему критерию требования объекта (субъекта) не удовлетворены: вместо оценки К nr имеется худшая оценка K nt ».
Дополнительные вопросы выбираются так, чтобы перебрать все возможные тройки критериев. Следовательно, количество дополнительных вопросов равно числу сочетаний из N по три ( C n 3 ).
Использование условия независимости в процедурах упорядочивания позволяет сократить количество вопросов к ЛПР.
Для иллюстрации процедур выявления предпочтений ЛПР обратимся к приведенному выше простому примеру. Основная процедура состоит в сравнении ценностей трех критериальных соответствий 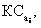 которые формируют следующие векторы соответствия:
которые формируют следующие векторы соответствия:
• по критерию «Профессиональная подготовленность» — вектор 100 { C 1 – O 1 };
• по критерию «Умение руководить коллективом» — вектор 010 {С 2 – О 2 };
• по критерию «Практический опыт» — вектор 001 {С 3 – О 3 }.
• Типовой вопрос, на который отвечает ЛПР, выглядит так:
Что вы предпочитаете:
Альтернатива 1. Неудовлетворение требований объекта лишь по критерию «Профессиональная подготовленность» – вместо высокой предлагается удовлетворительная оценка профессиональной подготовленности субъекта.
Альтернатива 2. Неудовлетворение требований объекта лишь по критерию «Умение руководить коллективом» – вместо хорошего предлагается удовлетворительное умение субъекта руководить коллективом.
Выберите один из ответов:
Альтернатива 1 более предпочтительна.
Альтернатива 2 более предпочтительна.
Альтернативы равноценны.
В основной процедуре анализируются ответы на три подобных вопроса. В дополнительной процедуре, применяемой при абсолютных критериальных соответствиях, для рассматриваемого примера необходим дополнительный вопрос, который отличается от приведенного выше дополнительным условием: «Для обеих альтернатив по критерию «Практический опыт» у субъектов имеется низшая оценка – «Практический опыт отсутствует».
Если результаты сравнения, сделанного ЛПР, не зависят от КС а по третьему критерию, то делается вывод о выполнении условий независимости.
Заметим, что в рассматриваемом примере вторые компоненты критериальных соответствий 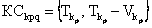 для первых двух критериев могут принимать ненулевые значения лишь в единственном случае, когда требования выражаются оценкой р=1, а возможности – оценкой q =2. Для третьего критерия, шкала которого содержит три оценки, таких возможностей уже три, из которых лишь одна реализуется в рассматриваемом примере (р=2, q =3).
для первых двух критериев могут принимать ненулевые значения лишь в единственном случае, когда требования выражаются оценкой р=1, а возможности – оценкой q =2. Для третьего критерия, шкала которого содержит три оценки, таких возможностей уже три, из которых лишь одна реализуется в рассматриваемом примере (р=2, q =3).
В зависимости от типа задачи либо может быть построена упорядоченная шкала всех оценок по данному критерию, либо могут быть упорядочены КС а , встречающиеся только в данной конкретной задаче. В общем случае для шкалы критерия с N оценками существует N ( N – l )/2 возможностей, которые необходимо проанализировать.
Обратимся к рассматриваемому примеру. Пусть ЛПР, анализируя назначения {С 1 – О 1 }, {С 2 – О 2 }, {С 3 – О 3 } с векторами соответствия 100, 010 и 001, упорядочил ценности КС а следующим образом:
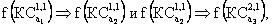
что для первой пары интерпретируется в виде: вектор соответствия, у которого первый компонент равен 1 при оценке по шкале требований, равной 1, а остальные компоненты равны нулю, предпочтительнее вектора, второй компонент которого при тех же требованиях равен 1, а остальные компоненты равны нулю; а для второй пары – в виде: вектор соответствия, у которого второй компонент равен 1 при оценке по шкале требований, равной 1, а остальные компоненты равны нулю, предпочтительнее вектора, третий компонент которого равен 1 при оценке по шкале требований, равной 2 , а остальные компоненты равны нулю.
При выполнении условия независимости, учитывая транзитивность 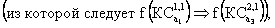 эти результаты можно использовать для упорядочения ряда назначений без обращения к ЛПР.
эти результаты можно использовать для упорядочения ряда назначений без обращения к ЛПР.
| C 1 | C 2 | C 3 | |||
| O 1 | 100 | ? | 110 | ? | 111 |
| n | i i | n | i i | n | |
| O 2 | 000 | ? | 010 | ? | 011 |
| i | n | i i | n | ||
| O 3 | 000 | 000 | ? | 001 |
Рис. 4.1. Функция полезности для критерия
C 1 «Стоимость постройки аэропорта»
На основании такого рода отношений большинство назначений могут быть упорядочены по качеству. Так, для приведенного выше примера можно построить граф, показанный на рис. 12.1.
В рассматриваемом примере формально остается невыясненным лишь отношение между назначениями {С 2 – О 1 } и {С 3 – О 2 }, определение которого требует обращения к ЛПР. Однако и это отношение может быть получено, если будет выяснено, что условие независимости выполняется. Тогда, поскольку 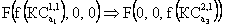 и это отношение не может измениться от наличия одинакового КС а по второму критерию у сравниваемых векторов, имеем
и это отношение не может измениться от наличия одинакового КС а по второму критерию у сравниваемых векторов, имеем
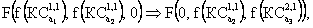
т. е. 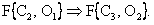
Аналогичные графы могут быть построены и в общем случае. Назовем их графами частичного упорядочения векторов соответствия по их ценности для ЛПР. Графы частичного упорядочения векторов соответствия позволяют перейти к ранжированию этих векторов по ценности.
Выделим в графе все недоминируемые векторы и назовем их первым ядром. Среди векторов, оставшихся после удаления первого ядра, выделим второе ядро, состоящее из недоминируемых векторов в редуцированном пространстве. Этот процесс повторяется до исчерпания графа [ 17 ]. Вектору, входящему в i - e ядро, присваивается i -й ранг, если над ним доминирует вектор из ( i – l )-г o ядра, а он сам доминирует над вектором из ( i + l )-г o ядра. Если вектор входит в i - e ядро и доминирует над вектором из ( i + p )-г o ядра, то его ранг размыт и находится в пределах от ( i +1) до ( i + p –1).
Процедура ранжирования для рассматриваемого примера приводит к следующему результату:
| Ядро | Список назначений | Ранг |
| 1 | {C 1 – O 2 } {C 1 – O 3 } {C 2 – O 3 } | 0 |
| 2 | {C 1 – O 1 } | 1 |
| 3 | {C 2 – O 2 } | 2 |
| 4 | {C 2 – O 1 } {C 3 – O 3 } | 3 |
| 5 | {C 3 – O 2 } | 4 |
| 6 | {C 3 – O 1 } | 5 |
Получим для рассматриваемого примера табл. 12.5, отражающую упорядочение назначений по качеству (высшее качество — идеальное назначение — имеет высший ранг, которому присвоено значение 0, при снижении качества уменьшается ранг назначения и соответственно увеличивается его номер, т. е. число, отображающее качество).
Таблица 12.5. Ранги назначений
| C 1 | C 2 | C 3 | |
| O 1 | 1 | 3 | 5 |
| O 2 | 0 | 2 | 4 |
| O 3 | 0 | 0 | 3 |
В результате выполнения основной и вспомогательной процедур выявления предпочтений назначения ранжируются по их ценности для ЛПР.
Выше была проиллюстрирована основная процедура выявления предпочтений ЛПР для абсолютных критериальных отклонений. Покажем, каким могло бы быть решение рассматриваемого примера при анализе относительных критериальных отклонений. Первый этап такого анализа прост и не требует участия ЛПР. Действительно, из анализа таблицы сходства (см. табл. 12.2) и учета свойств функции ценности следует упорядочение всех объектов по отношению к каждому из субъектов, и наоборот. Суммируя полученные при таком ранжировании ранги (высший ранг равен 0), получаем табл. 12.6.
Таблица 12.6.Ранги назначений при относительных соответствиях
| C 1 | C 2 | C 3 | |
| O 1 | 1 | 3 | 4 |
| O 2 | 0 | 2 | 3 |
| O 3 | 0 | 0 | 1 |
В соответствии с критерием оптимальности ЛПР утверждает очевидное решение: [{ C 1 – O 2 } { C 2 – O 3 } { C 3 – O 1 }].
Как правило, количество вопросов к ЛПР при анализе относительных критериальных соответствий меньше, чем при анализе с использованием абсолютного индекса соответствия.
Дата: 2019-02-19, просмотров: 356.