Основной целью данного этапа является поиск возможности идеального решения МЗН и выработка рекомендаций по стратегии дальнейшего решения МЗН.
Сначала преобразуются исходные данные, затем проверяется существование идеальных назначений, при которых взаимные требования пары объект–субъект полностью удовлетворены.
Идеальные назначения формируют область поиска идеального решения МЗН. Если удается найти n идеальных пар, дающих полное решение задачи, то это означает, что идеальное решение МЗН, удовлетворяющее всем требованиям, получено без вмешательства ЛПР и анализ проблемы закончен.
При решении МЗН используются не только абсолютные, но и относительные оценки элементов двух множеств. Иначе говоря, характеристики элементов рассматриваются относительно характеристик предполагаемых партнеров, которые являются претендентами на назначение. Для каждого элемента первого множества определяется степень соответствия его характеристик характеристикам элементов второго множества, и наоборот. На основе анализа таких соответствий делается попытка определить качество назначения. На данном этапе используется формальный индекс соответствия, вычисляемый на основе исходных данных без участия ЛПР.
Формально отношения между элементами двух множеств (субъектов и объектов) могут быть охарактеризованы вектором соответствия R ij ( i , j = l ,2,..., n ), k -й компонент которого отражает степень соответствия характеристик элементов по k -му критерию. Таким образом, на этапе анализа данных эквивалентом понятия «критериальное соответствие по k -му критерию» является компонент вектора соответствия, который подсчитывается следующим образом:
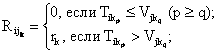
здесь 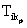 – требование i -г o элемента одного множества (субъекта или объекта), выражаемое р-й по порядку оценкой на шкале требований по k -му критерию;
– требование i -г o элемента одного множества (субъекта или объекта), выражаемое р-й по порядку оценкой на шкале требований по k -му критерию; 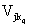 – соответствующие возможности j -г o элемента другого множества, выражаемые q -й оценкой на шкале возможностей того же k -го критерия; r k – число оценок на шкале k -го критерия, на которой требования превышают возможности.
– соответствующие возможности j -г o элемента другого множества, выражаемые q -й оценкой на шкале возможностей того же k -го критерия; r k – число оценок на шкале k -го критерия, на которой требования превышают возможности.
Поскольку оценки на шкале имеют две формулировки (см.выше) и упорядочены от лучшей к худшей, то 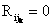 , если р > q , где p , q – номера оценок на шкалах требований и возможностей k -го критерия. Таким образом, условие
, если р > q , где p , q – номера оценок на шкалах требований и возможностей k -го критерия. Таким образом, условие 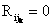 означает, что требования по k -му критерию удовлетворены, а условие
означает, что требования по k -му критерию удовлетворены, а условие 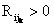 – неудовлетворенность требований. Если требования по k -му критерию удовлетворены, то по определению КС по этому критерию является идеальным и обладает наивысшим качеством.
– неудовлетворенность требований. Если требования по k -му критерию удовлетворены, то по определению КС по этому критерию является идеальным и обладает наивысшим качеством.
В то же время для анализа этого этапа важен лишь факт, указывающий на то, что возможности удовлетворяют (или превышают) выдвинутым требованиям, а степень удовлетворения требований несущественна. Поэтому естественно принять, что оценки возможностей, превышающие уровень удовлетворения требований, «одинаково хороши», поскольку позволяют отнести назначение с идеальными по каждому критерию КС к идеальному назначению.
Множество векторов соответствия R ij образует ( n ? n ) таблицу сходства, в клетке ( i , j ) которой помещен вектор соответствия субъекта C i и объекта O j .
На данном этапе для каждого вектора соответствия формируется агрегированный критерий – свертка вектора соответствия. Введем следующие обозначения элементов свертки вектора соответствия: значение 0 соответствует паре с полностью взаимно удовлетворенными требованиями по всем критериям, значение 1 – не удовлетворено одно из требований, причем степень неудовлетворенности соответствует одной градации шкалы 2 – не удовлетворено одно из требований на две градации шкалы, либо два различных требования – на одну градацию каждое и т.д.
Предполагая равноценность компонентов вектора соответствия и их шкал, значение свертки вычисляют как сумму отклонений по каждому из компонентов вектора соответствия. Тогда суммарная величина критериальных соответствий 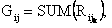 k =1,2,..., N , при сделанных выше предположениях может служить формальным индексом качества назначения, которое является наилучшим при G ij = 0 (идеальное назначение) и ухудшается с увеличением G ij .
k =1,2,..., N , при сделанных выше предположениях может служить формальным индексом качества назначения, которое является наилучшим при G ij = 0 (идеальное назначение) и ухудшается с увеличением G ij .
Следствием предположения о равной важности критериев и их шкал является вывод о том, что существует единая шкала качества назначений. При этом назначения, имеющие одинаковое значение свертки, равноценны, т.е. обладают равным качеством. Таким образом, в рамках сделанных на данном этапе предположений качество назначения монотонно меняется с изменением значения свертки, т. е. качество назначения по определению равно значению G ij формального индекса соответствия.
Для того чтобы реализовать цель этапа анализа данных – проверить, возможно ли идеальное решение МЗН, воспользуемся решением однокритериальной задачи о назначениях (ЗН) на множестве элементов таблицы формальных индексов соответствия. Решение ЗН, полученное для минимума суммы значений агрегированных критериев (максимизирующее суммарное качество назначений), является идеальным решением МЗН, если минимум равен нулю. Формальной оценкой качества решения может служить значение достигнутого минимума (т. е. суммарное качество назначений, входящих в окончательное решение).
Проиллюстрируем применение процедур этапа анализа данных на приведенном выше примере. Исходные данные – оценки по критериям трех субъектов и трех объектов – можно представить в виде табл. 12.1.
Таблица 12.1.Значения оценок по критериям субъектов и объектов
| Субъект | Критерии | Объект | Критерии | ||||
| K 1 | K 2 | K 3 | K 1 | K 2 | K 3 | ||
| C 1 | 2 | 1 | 2 | C 1 | 1 | 1 | 2 |
| C 2 | 2 | 2 | 2 | C 2 | 2 | 1 | 2 |
| C 3 | 2 | 2 | 3 | C 3 | 2 | 2 | 2 |
Таблица сходства, составленная из векторов соответствия, имеет вид табл. 12.2. Легко увидеть, что при заданных условиях существуют три идеальных назначения (векторы со всеми нулевыми компонентами): { C 1 – O 2 }; { C 1 – O 3 }; { C 2 – O 3 }.
Таблица 12.2.Векторы соответствия
| C 1 | C 2 | C 3 | |
| O 1 | 100 | 110 | 111 |
| O 2 | 000 | 010 | 011 |
| O 3 | 000 | 000 | 001 |
Для того чтобы проверить, возможно ли идеальное решение МЗН, сформируем таблицу формальных индексов соответствия. Таблица сходства (см. табл. 12.2) может быть представлена в виде таблицы свертки (табл. 12.3).
Таблица 12. 3.Индексы соответствия
| C 1 | C 2 | C 3 | |
| O 1 | 1 | 2 | 3 |
| O 2 | 0 | 1 | 2 |
| O 3 | 0 | 0 | 1 |
Воспользуемся решением однокритериальной ЗН на множестве элементов этой таблицы. Из решения задачи следует, что в приведенном примере идеального решения МЗН не существует. Любое возможное решение для рассматриваемого примера содержит, по меньшей мере, одно неидеальное назначение. Например, решение [{ C 1 – O 2 } { C 2 – O 3 } { C 3 – O 1 }] включает назначение { C 3 – O 1 }, отличное от идеального ( G 31 =3). Следовательно, для рассматриваемого примера процедуры поиска решения МЗН должны быть продолжены.
В диалоге ЛПР с системой выясняются основные характеристики рассматриваемой задачи, касающиеся уникальности и размерности задачи, а также мнение ЛПР относительно типа задачи; предлагаются те или иные стратегии поиска решения.
Ниже мы обсудим, каким образом ЛПР может воспользоваться рекомендациями системы при выборе стратегии поиска решения в зависимости от характера и типа задачи.
Дата: 2019-02-19, просмотров: 378.