При появлении многокритериальных задач возникли доп олнительные трудности их решения, связанные с получением информации от ЛПР. Естественной реакцией на это было стремление получить такую информацию сразу я быстро устран ить многокритериальность. Этот подход был реализован путем объединения многих критериев в один с помощью так назы- ваемых весовых коэффициентов важности критериев. Глоб альный критерий вычисляется по формуле

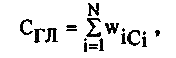(1)

где Ci - частные критерии ( i = 1, ..., N); wi - веса (коэффициенты важности) критериев:

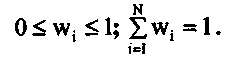(2)

Идея такого объединения состоит в том, что ЛПР назначает числа (часто по численной шкале 1—100), представляющие для арго ценность рассматриваемого критерия. Считается, что ЛПР может назначить такие числа. Далее, весовые коэффициенты нормируются на основе условия (2).

Обратимся к рис. 3.2. Легко увидеть, что решения, соотв етствующие точкам А и В на множестве Эджворта-Парето, могут быть представлены в виде

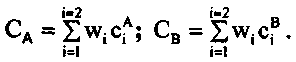
Существует лемма [8], утверждающая, что для линейной задачи любое эффективное, находящееся на множестве Э—П, решение может быть представлено как решение задачи линейн ого программирования с критерием (1). Следовательно, форм ально задача сводится к нахождению весов.

Возникла идея, что эти веса можно получить от ЛПР опер ативно. Если ЛПР затрудняется в начале процесса решения (до изучения области В) сразу назвать эти веса, то можно построить ЧМП следующего содержания: ЛПР назначает первоначальные веса, смотрит на решение и корректирует веса до получения удовлетворительного результата.

Классификация ЧМП

В [3] предложена классификация ЧМП, основанная на хар актере информации, получаемой от ЛПР на фазе анализа.

Первая группа ЧМП — прямые ЧМП, в которых ЛПР непос редственно назначает веса критериев и корректирует их на основе полученных решений.

Для второй группы ЧМП задача ЛПР состоит в сравнении многокритериальных решений. Эта группа называется ЧМП оценки векторов.

Третья группа требует от ЛПР наложения ограничений на значения критериев и, следовательно, на область достижимых значений. ЧМП этой группы называются ЧМП поиска удовлет ворительных решений.

Перед тем как перейти к рассмотрению ЧМП каждой групп ы, следует указать на общие предварительные этапы,встре чающиеся во многих ЧМП. Прежде всего рекомендуется произ­ вести нормирование критериев, определив диапазон их измене ния от 0 до 1:

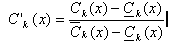
где 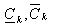— минимально и максимально возможные значения k -го критерия; Ck (х) — промежуточное значение.

Кроме того, как это было показано выше (табл. 3.1), для каждого из критериев вычисляется наилучшее значение при предположении, что он является единственным. Вектор таких (недостижимых одновременно) значений помогает ЛПР оценить пределы возможного.