Возникает вопрос, всегда ли и насколько необходимо учи­тывать нерациональность поведения людей в задачах экономического выбора?

Одной из важнейших в экономике задач является задача предсказания поведения потребителя по отношению к конкрет ным группам товаров или услуг. Знание такого поведения по­ зволяет определить спрос на товар (услугу), подсчитать, сколь­ ко нужно производить товаров (услуг) и по какой цене их можно продавать.

Экономисты различают наблюдаемые предпочтения и вы­ являемые предпочтения потребителей. Наблюдаемые предпочтения определяются на основе изучения данных о покупках и продажах. Строятся математические модели, описывающие спрос покупателей на определенные товары (услуги). Такие мо­дели позволяют предсказать поведение покупателей по отно­ шению к данному товару (услуге) или близким к нему [10].

Знание человеческого поведения, человеческих эвристик не дает ничего нового при определении наблюдаемых предпочтений. Действительно, пусть поведение потребителей отличается от рационального - модель опишет такой вид поведения по на блюдаемому выбору. Ее прогностические способности не изме нятся. Пусть, например, известно, что выбор отдельным поку­ пателем сорта чая осуществляется нерационально. Но для про­ изводителей чая важны лишь данные о спросе на тот или иной сорт чая для большой группы покупателей (жителей города, области и т.д.). Зависимость спроса на чай от его цены опреде­ ляется для группы в целом, и на нее мало влияет, насколько рациональны люди при покупке чая.

По-иному обстоит дело с выявляемыми предпочтениями, когда требуется предсказать спрос на основе опроса (мнений) потребителей еще до их выбора. Ясно, что результаты психоло­гических исследований имеют непосредственное и весьма важное значение при выявлении предпочтений потребителей. Для получения надежных данных на основе выявляемых предпоч­ тений необходимо строить опросы с учетом человеческих эври­ стик [10]. Особое значение имеет форма постановки вопро­ сов, возможные влияния точки отсчета, феномен сверхуверенности и т.д.

При анализе решений производителей товаров (и услуг) знание нерационального человеческого поведения также весьма важно. Правда, существует мнение [11], что рынок приучает к рациональности, что значительные отклонения от рациональ­ности могут привести к разорению ЛПР. Однако это не позво­ляет определить, насколько успешно такое обучение.

Стремление учесть реальное поведение людей и приблизить теорию к жизни привело к появлению теории проспектов, раз­работанной А. Тверским и Д. Канеманом [12, 13].

Теория проспектов

Теория проспектов была разработана для того, чтобы учесть реальные черты человеческого поведения в задачах с субъективными вероятностными оценками. Ставилась цель за­ менить теорию ожидаемой полезности в качестве средства, по­ зволяющего человеку выбирать предпочтительные варианты действий.

Теория проспектов позволяет учесть три поведенческих эффекта:

• эффект определенности, т.е. тенденцию придавать боль ший вес детерминированным исходам;
• эффект отражения, т.е. тенденцию к изменению пред почтений при переходе от выигрышей к потерям;
• эффект изоляции, т.е. тенденцию к упрощению выбора путем исключения общих компонентов вариантов решений.

Рассмотрим игру (х, р, у, q ), где исход х осуществляется с вероятностью р, исход у — с вероятностью q , а нулевой исход — с вероятностью 1-р- q (рис. 2.10). В теории проспектов игра, представленная на рисунке, называется проспектом. Оценива­ ется ценность (а не ожидаемая полезность) этой игры по сле­ дующей формуле:

V = V ( x ) xor П(р)+ V (у) xor П( q ),

где V ( x ), V ( y ) - ценность исходов х, у соответственно, V (0)=0 и П(р), П( q ) - вес (важность) вероятностей р, q соответственно.

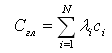
Рис. 2.10. Представление проспекта

Мы видим первое отличие теории проспектов: вместо веро ятностей используется функция от вероятностей.

Проанализируем другие отличия теории проспектов от тео­ рии полезности. Во-первых, полезность в теории полезности определялась как прибавление (может быть, и отрицательное) к первоначальному благосостоянию человека. Ценность же от считывается от любого уровня, принятого за исходный. Во- вторых, предполагается (для учета поведенческих аспектов), что функция V ( x ) ценности - выпуклая для выигрышей и во гнутая для потерь (рис. 2.11), причем ее изменение для потерь будет больше, чем для выигрышей.

Важное различие двух теорий состоит в учете вероятностей исходов. Если в теории полезности вероятность умножается на полезность исхода, то в теории проспектов используется функ ция вероятности П(р), представленная на рис. 2.12. Эта функ­ ция также построена специальным образом для учета поведен­ ческих аспектов. Прежде всего П(р) не подчиняется всем зако­ нам теории вероятностей. Отметим следующие свойства П(р):

• П(0)=0, П(1)=1;
• П(р)+П(1-р) < 1;
• при малых вероятностях П(р) > р;
• отношение П( p )/П( q ) ближе к единице при малых веро ятностях, чем при больших;
• П(р) плохо определена у крайних значений.

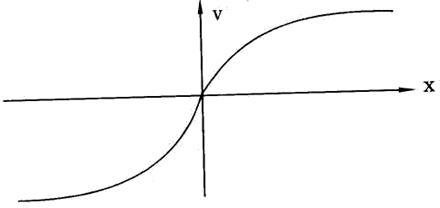
Рис. 2.11. Функция ценности

Вес вероятности

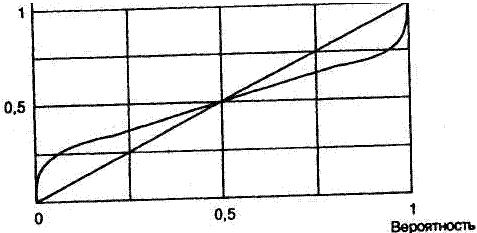
Рис. 2.12. Весовая функция вероятности

Теперь мы можем привести последовательность этапов, ре­ комендуемую при применении теории проспектов для выбора между различными вариантами действий.

1. Осуществляется редактирование проспекта; этап опреде лен достаточно неформально. В него входит следующее:

• выбирается опорная точка;
• одинаковые исходы объединяются, и их вероятности сумми руются;
• одинаковые исходы с равными вероятностями в сравнивае мых играх удаляются;
• доминируемые исходы удаляются;
• округляются значения ценностей и вероятностей.

2. Подсчитываются значения ценности для разных вариан тов действий по формуле, приведенной выше, после чего выби рается вариант с наибольшей ценностью.