В [1] вводится шесть аксиом и доказывается существование функции полезности. Дадим содержательное представление этих аксиом. Обозначим через х, у, z различные исходы (результаты) процесса выбора, а через р, q -вероятности тех или иных исхо дов. Введем определение лотереи. Лотереей называется игра с двумя исходами: исходом х, получаемым с вероятностью р, и исходом у, получаемым с вероятностью 1-р (рис. 2.1).
Примером лотереи является подбра сывание монеты. При этом, как известно, с вероятностью р=0,5 выпадает орел или решка. Пусть х=$10 и у= -$10 (т. е. мы получаем $10 при выпадении орла и пла тим столько же при выпадении решки). Ожидаемая (или средняя) цена лотереи определяется по формуле рх+(1—р)у. Приведем аксиомы рационального выбора.
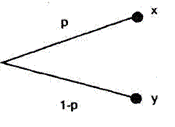
Рис. 2.1. Представление лотереи
Аксиома 1. Исходы х, у, z принадлежат множеству А ис ходов.
Аксиома 2. Пусть Р означает строгое предпочтение (похо жее на отношение > в математике); R — нестрогое предпочте ние (похожее на отношение >); I — безразличие (похожее на отношение =). Ясно, что R включает Р и I . Аксиома 2 требует выполнения двух условий:
- связности: либо xRy , либо yRx , либо то и другое вместе;
- транзитивности: из xRy и yRz следует xRz .
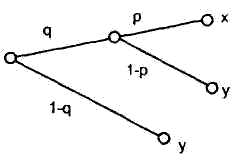
Аксиома 3. Две представленные на рис. 2.2 лотереи находятся в отношении безразличия.
Справедливость этой аксиомы очевидна. Она записывается в стандартном виде как ((х, р, y ) q , y ) I ( x , pq , у). Здесь слева представлена сложная лотерея, где с вероятностью q получаем простую лотерею, в которой с вероятностью р получаем исход х или с вероятностью (1-р) - исход у), и с вероятностью (1-q) - исход у.
Аксиома 4. Если xIy , то (х, р, z ) I (у, р, z ).
Аксиома 5. Если хРу, то хР(х, р, у)Ру.
Аксиома 6. Если xPyPz , то существует вероятность р, такая, что у I (х, р, z ).
 I
I 
Рис. 2.2. Две лотереи, находящиеся в отношении безразличия
Все приведенные выше аксиомы достаточно просты для по нимания и кажутся очевидными.
В предположении, что они выполняются, была доказана следующая теорема [1]: если аксиомы 1-6 удовлетворяются, то существует числовая функция полезности U , определенная на А (множество исходов) и такая, что:
- xRy тогда и только тогда, когда U ( x ) ? U ( y ).
- U ( x , р, у) = pU ( x )+( l - p ) U ( y ).
Функция U ( x ) - единственная с точностью до линейного преобразования (например, если U ( x ) ? U ( y ), то и a + U ( x ) ? a + U ( y ), где а — целое положительное число).
Задачи с вазами
Теория полезности экспериментально исследовалась в так называемых задачах с вазами (или урнами). Ваза - это непрозрачный сосуд, в котором находится определенное (известное лишь организатору эксперимента) количество шаров различно го цвета. Задачи с вазами типичны для группы наиболее простых задач принятия решений — задач статистического типа. Для решения этих задач надо знать элементарные начала тео рии вероятностей [4]. Человек делает выбор в этих задачах, основываясь на расчетах. Варианты действий выражены в наибо лее простом виде.
Типовая задача для испытуемого может быть представлена следующим образом [3]. Перед испытуемым ставится ваза, ко торая может быть вазой 1-го или 2-го типа. Дается следующая информация: сколько имеется у экспериментатора ваз 1-го и 2-го типов; сколько черных и красных шаров в вазах 1-го и 2-го типов; какие выигрыши ожидают испытуемого, если он угадает, какого типа ваза; какие проигрыши ожидают его, если он ошибется. После получения такой информации испытуемый должен сделать выбор: назвать, к какому типу принадлежит поставленная перед ним ваза.
Пусть, например, экспериментатор случайно выбирает вазу для испытуемого из множества, содержащего 700 ваз 1-го типа и 300 ваз 2-го типа. Если перед испытуемым находится ваза 1-го типа и он угадает это, то получит выигрыш 350 денежных единиц (д.е.), если не угадает, его проигрыш составит 50 д.е. Если перед ним ваза 2-го типа и он это угадает, то получит вы игрыш 500 д.е., если не угадает, его проигрыш составит 100 д.е. Примем, что полезность для испытуемого равна каче ству денежных единиц. Испытуемый может предпринять одно из следующих действий: d 1 - сказать, что ваза 1-го типа; d 2 —сказать, что ваза 2-го типа.
Условия задачи можно представить в табл. 2.1.
Таблица 2.1. Представление задачи с вазами
| Тип вазы | Вероятность выбора вазы данного типа | Действия и выигрыши | |
| d 1 | d 2 | ||
| 1 | 0.7 | 350 | -100 |
| 2 | 0.3 | -50 | 500 |
Что же делать человеку? Теория полезности отвечает: оценить среднюю (ожидаемую) полезность каждого из действий и выбрать действие с максимальной ожидаемой полезностью. В соответствии с этой рекомендацией мы можем определить среднее значение выигрыша для каждого из действий:
U ( d 1 ) = 0,7 xor 350 - 0,3 xor 50 = 230 д.е;
U ( d 2 ) = 0,3 xor 500 - 0,7 xor 100 = 80 д.е.
Следовательно, разумный человек выберет действие d 1 а не действие d 2 .
Из этого примера следует общий рецепт действий для ра ционального человека: определить исходы, помножить их на соответствующие вероятности, получить ожидаемую полезность и выбрать действие с наибольшей полезностью.
Задачи с вазами помогут нам познакомиться с построением деревьев решений и принятием решений с их помощью.
Деревья решений
Приведенная выше табл. 2.1 может быть представлена в виде дерева решений (рис. 2.3). На этом дереве квадратик озна чает место, где решение принимает человек, а светлый кру жок - место, где все решает случай. На ветвях дерева написа ны уже знакомые нам значения вероятностей, а справа у конеч ных ветвей - значения исходов (результаты).
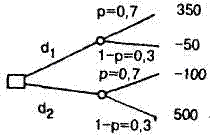
Рис. 2.3. Дерево решений
Для чего нужно дерево решений? Мы можем использовать его для представления своих возможных действий и для нахо ждения последовательности правильных решений, ведущих к максимальной ожидаемой полезности. Чтобы показать это, ус ложним задачу. Пусть в вазе 1-го типа содержится 6 красных и 4 черных шара. В вазе второго типа содержится 3 красных и 7 черных шаров. Предоставим человеку, выбирающему между действиями d 1 и d 2 , дополнительные возможности. Пусть он может до своего ответа вытащить за определенную плату один шар из вазы, причем после вытаскивания шар кладется обратно в вазу. Плата за вытаскивание одного шара равна 60 д. е.
Дерево решений с двумя его основными ветвями представ лено на рис. 2.4. Вот теперь вопрос о том, какое решение сле дует принимать, стал сложнее: необходимо решить, стоит ли вынимать шар и какой ответ дать после вытаскивания красно го или черного шара. При принятии этих решений нам окажет существенную помощь известный в теории вероятностей [4] (и в теории статистических решений) способ подсчета изменения вероятностей событий после получения дополнительной ин формации.
Вернемся к описанию задачи. Вероятность вытащить крас ный шар из вазы 1-го типа p K ( B 1 )=0,6, а из вазы 2-го типа p к (В 2 )=0,3. Зная все условные вероятности (зависящие от усло вия), а также вероятности p 1 и p 2 выбора ваз 1-го и 2-го типа (см. табл. 2.1), мы можем поставить следующие вопросы.
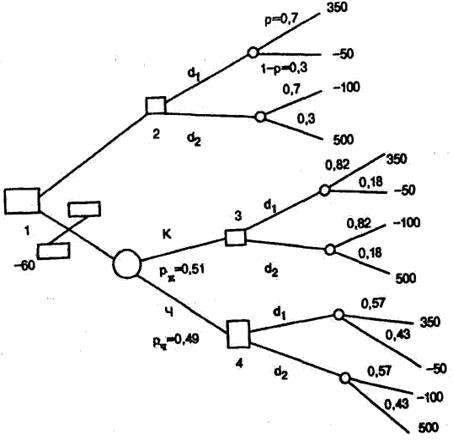
Рис. 2.4. Дерево решений
Первый вопрос: каковы вероятности вытащить красный и черный шары? Для ответа на этот вопрос произведем простые вычисления. Вероятность вытащить красный шар: p K ( B 1 )=0,7 A 0,6=0,42, если ваза окажется 1-го типа, p к (В 2 )=0,3 A 0,3=0,09, если ваза окажется 2-го типа. Следовательно, вероятность вы тащить красный шар в общем случае р к =0,51. Аналогичным образом можно посчитать, что вероятность вытащить черный шар Рч=0,49.
Второй вопрос более сложный. Пусть вытащенный шар оказался красным (черным). Какое действие следует выбрать: d 1 или d 2 ? Для ответа на этот вопрос нужно знать вероятности принадлежности ваз к 1-му и 2-му типам после получения до полнительной информации. Эти вероятности позволяет опреде лить знаменитая формула Байеса [4].
Например, мы вытащили красный шар. Какова после этого вероятность того, что перед нами стоит ваза 1-го типа?
Приведем все обозначения вероятностей:
- p k ( B 1 ) - вероятность вытащить красный шар из вазы 1-го типа;
- p ч ( B 1 ) — вероятность вытащить черный шар из вазы 1-го типа;
- p к(В 2 ) ~ вероятность вытащить красный шар из вазы 2-го типа;
- p ч (В 2 ) — вероятность вытащить черный шар из вазы 2-го типа;
- p ( B 1 ) - вероятность того, что ваза окажется 1-го типа;
- р(В 2 ) - вероятность того, что ваза окажется 2-го типа;
- p ( B 1/ K ) - вероятность того, что ваза окажется 1-го типа по сле вытаскивания красного шара;
- p ( B 1/ч ) - вероятность того, что ваза окажется 1-го типа после вытаскивания черного шара;
- р(В 2/к ) - вероятность того, что ваза окажется 2-го типа по сле вытаскивания красного шара;
- p (В 2/ч ) - вероятность того, что ваза окажется 2-го типа по сле вытаскивания черного шара.
Формула Байеса позволяет оценить p ( B i / K ) и p ( B i /ч ), где i =1, 2, используя все прочие вероятности. Например:
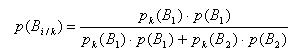
Для нашей задачи: p ( B 1/ K )=0,82; p ( B 1/ч )=0,57; p ( B 2/ K )=0,18; р(В 2/ч )=0,43.
Теперь мы имеем всю информацию, необходимую для при нятия решений.
На рис. 2.4 показаны две основные ветви дерева решений, причем верхняя просто повторяет дерево решений на рис. 2.3. Квадратик 1 слева соответствует первому решению - вытаски вать шар или нет. Случаю отказа от вытаскивания шара соот ветствует верхняя основная ветвь. Решению вытаскивать шар соответствует нижняя ветвь, начинающаяся со случайного со бытия (кружок). В квадратиках 2, 3, 4 принимаются решения о выборе одной из двух стратегий: d 1 или d 2 . Далее все решает случай (кружки).
Есть три простых правила выбора оптимальной (по крите-, рию максимума ожидаемой полезности) последовательности ре-шений на основе дерева решений:
• идти от конечных ветвей дерева к его корню;
• там, где есть случайность (кружок), находится среднее значение;
• там, где есть этап принятия решений (квадратик), выбирается ветвь с наибольшей ожидаемой полезностью, а другая отсекается двумя черточками.
Применим эти правила к дереву решений, представленному на рис. 2.4. В результате получим дерево решений, показанное на рис. 2.5.
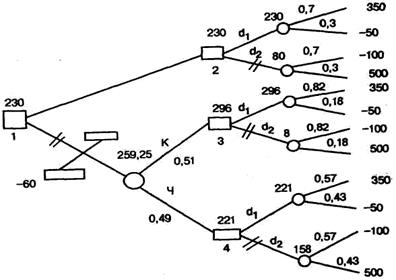
Рис. 2.5. «Сворачивание» дерева решений
На этом рисунке над кружками указаны средние значения полезности, двумя черточками отсечены ветви с меньшим значением ожидаемой полезности. Наилучший вариант действий: шар не вытаскивать и выбирать действие d 1 . Этот вариант соот ветствует самому верхнему пути дерева решений на рис. 2.5. Такая процедура нахождения оптимального пути на деревьях решений получила название «сворачивание» дерева решений.
Деревья решений при заданных числовых значениях веро ятностей и исходов позволяют осуществить выбор той страте гии (последовательности действий), при которой достигается наибольший выигрыш, т.е. достигается максимум функции по лезности ЛПР.
Парадокс Алле
Возникают вопросы: нельзя ли заменить ЛПР автоматом? Сохраняются ли при сворачивании дерева решений какие-то особенности человеческого поведения? Для ответа на эти во просы приведем известный парадокс Алле [3] (предложенный французским ученым М. Алле), представленный двумя лоте реями на рис.2.6.
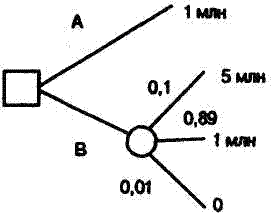
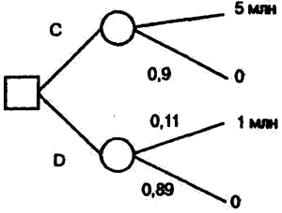
Рис. 2.6. Парадокс Алле
Обозначим: U (5 млн)=1; U ( l млн)= U ; U (0)=0. В левой лоте рее есть выбор между действиями А (получить 1 млн) и В (со гласиться на лотерею). В экспериментах подавляющее боль шинство людей предпочитает А. Из этого следует U > 0, l A l + 0,89 A U или U >10/ ll .
В правой лотерее есть выбор между действиями С и D (две лотереи). Подавляющее большинство людей предпочитает действие С (почти та же вероятность проиграть, но выигрыш больше). Тогда 1 A 0,1>0,11 A U , т.е. U <10/ ll . Совершая такой выбор, лю ди действуют не в соответствии с функцией полезности.
Приведем еще один пример. Рассмотрим две лотереи, пока занные на рис. 2.7. Легко убедиться в том, что средняя цена лотерей одинакова. Но это не означает, что людям безразлично, какую из них выбрать. Подчеркнем, что свобода выбора остается за ЛПР. Предъявление различным группам людей лотерей показало, что люди предпочитают правую лотерею, где при той же средней цене риск проигрыша исключен.
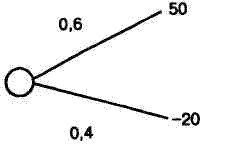
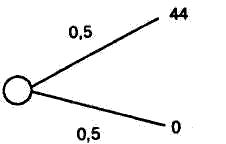
Рис. 2.7. Сравнение двух лотерей
Как же можно объяснить такое поведение людей? Может быть, стоит усомниться в существовании функции полезности? Этот вопрос становится еще более существенным для задач принятия решений, в которых нет информации для объектив ного подсчета вероятностей. В таких задачах (а их гораздо больше, чем формальных задач с вазами) только эксперты мо гут дать значения вероятностей. Ясно, что эти значения субъ ективны. Потребовалось формальное обоснование теории по лезности с субъективными вероятностями — теории субъектив ной ожидаемой полезности [5]. Она также построена аксиома тически.
Но и после построения этой теории остаются те же вопросы о причинах парадоксального поведения людей в задачах при нятия решений, где в качестве метода выбора использовались деревья решений и максимизация субъективной ожидаемой полезности.
Дата: 2019-02-19, просмотров: 457.