Эти процедуры также предназначены для систематического поиска наилучшего решения. Однако такой поиск осуществляется по-иному: в порядке очереди определяется приемлемое значение по каждому из критериев.
Примером ЧМП поиска удовлетворительных значений крит ериев служит процедура STEM — одна из первых ЧМП [11]. Она предназначена для решения многокритериальных задач линейного программирования, одной из которых как раз и явл яется многокритериальная транспортная задача (см. выше).
Рассмотрим фазы расчетов и анализа ЧМП STEM .
Фаза расчетов
1. Проводится оптимизация по каждому критерию отдель но, при этом значения всех остальных критериев заносятся в табл. 3.2.
Таблица 3.2 Относительные значения критериев
| Критерий | C1 | C2 | ... | CN |
| С1 | 1 | C21 | ... | CN1 |
| С2 | C12 | 1 | ... | CN2 |
| ... | ... | ... | ... | ... |
| СN | C1N | C2N | ... | 1 |
В таблице C1j— значение 1-го критерия при оптимизации по j -му критерию. Ясно, что диагональные элементы равны един ице, а все прочие меньше единицы. Очевидно, что после норм ирования наибольшее значение каждого критерия равно един ице, а наименьшее - нулю. Любой столбец содержит значения соответствующего критерия, достигаемые при оптимизации по всем критериям.
В таблице представлена ценная информация, характеризующая область допустимых значений. Так, если значения как их-то двух столбцов близки для каждой из строк (кроме строк, содержащих единицы в этих столбцах), то два соответс твующих критерия сильно зависимы, так как изменения всех иных критериев (кроме этих двух) одинаково влияют на эти два критерия. Можно выявить также и противоречивые критер ии: высокая оценка по одному сопровождается низкой оценк ой по другому. Такая информация весьма полезна для ЛПР, изучающего возможности, предоставляемые областью D допуст имых значений.
2. По табл. 3.2 вычисляются индексы критериев.
Пусть ai — среднее значение, взятое по всем элементам i -го столбца (кроме единицы). Тогда li (индекс i -го критерия) вы числяется из соотношений:
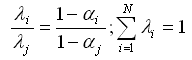 (3)
(3)
Индекс критериев может быть назван коэффициентом внимания, которое следует уделять критерию при поиске решения.
Предположим, что все элементы i -го столбца в табл. 3.2 близки к единице. Тогда среднее значение тоже близко к един ице, (1 — ai ) мало и соответствующий индекс мал. Действит ельно, если при оптимизации по другим критериям значение данного критерия близко к наилучшему, то ему вряд ли стоит уделять внимание. Наоборот, критерию, сильно зависящему от изменений других критериев (од мало), должны соответствовать большие значения индекса. Индексы называют иногда технич ескими весами потому, что в отличие от весов wi они не наз начаются ЛПР, а вычисляются.
3. Производится оптимизация по глобальному критерию. Глобальный критерий имеет вид
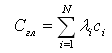 (4)
(4)
где li определяются из (3).
Решение, найденное при оптимизации, предъявляется ЛПР.
Фаза анализа
1. ЛПР анализирует вектор значений критериев у1 най денный при оптимизации по критерию (4). Затем ему задается
вопрос: все ли компоненты вектора y 1 имеют удовлетворитель ные значения? Если да, то решение получено. Если нет, то ЛПР указывает один критерий с наименее удовлетворительным значением. 2. ЛПР просят назначить для критерия с наименее удовле творительным значением пороговое значение h , при достиже нии которого можно признать этот критерий имеющим удовле творительное значение:
C >= 4 (5)
Условие (5) добавляется к совокупности линейных равенств и неравенств, определяющих область D допустимых значений переменных. Таким образом, возникает уже новая область доп устимых значений.
На этом фаза анализа заканчивается. Следующий шаг нач инается с фазы расчетов при новой области допустимых знач ений и т.д. При достижении удовлетворительных для ЛПР значений по всем критериям ЧМП останавливается.
Пример применения метода STEM : как управлять персоналом
Французской консультативной фирмой S Е M А предложена модель, характеризующая изменения со временем состава перс онала большой организации и продуктивности ее работы [12]. Модель применялась для прогнозирования последствий раз-личных вариантов управления кадрами организации. Проверялись разные стратегии приема на работу и повышения в должн ости через два, три и четыре года. В качестве переменных модели рассматривалось количество сотрудников, назначенных на различные должности в определенные периоды времени.
Использовались четыре критерия, представляющих собой линейные функции от переменных: общее «удовлетворение» кадров ( SA ); фактическая эффективность работы кадров ( EF ); стоимость приема на работу дополнительных сотрудников (ЕВ); стоимость нехватки кадров по отношению к прогнозируемым потребностям (ЕС).
В модель были заложены следующие зависимости: « эффективность работы сотрудника линейно зависит от отно-шения оценки его возможностей Q к оценке требований t , предъявляемых должностью к сотруднику; • удовлетворение сотрудника во время пребывания на определ енной должности сначала возрастает до максимального значения, а затем со временем уменьшается до первоначального значения также в зависимости от отношения Q к t .
С математической точки зрения проблема представляла собой задачу линейного программирования с четырьмя критер иями качества, 350 переменными и 200 ограничениями. Не имелось никакой априорной информации о сравнительной важности критериев.
Для решения был использован метод STEM [11]. На первом этапе решения в области допустимых значений была осуществл ена оптимизация по каждому из критериев. Затем при помощи линейного преобразования истинных значений критериев к значениям в интервале (ОД) (нормирования) был выполнен переход к относительным значениям критериев. Значения критериев при поочередной оптимизации по каждому из них приведены в табл. 3.3. Данные таблицы говорят о сильной зависимости критериев SA и EF и о противоречивости этих критериев и критериев ЕВ и ЕС; последние два противоречивы также друг другу.
Таблица 3.3 Значения критериев при поочередной оптимизации по каждому из них
| Критерии | SA | EF | EB | EC |
| SA | 1 | 0.875 | 0.275 | 0.83 |
| EF | 0.86 | 1 | 0.09 | 0.765 |
| EB | 0.131 | 0.149 | 1 | 0.4 |
| EC | 0.442 | 0.45 | 0.733 | 1 |
Далее на основе приведенной таблицы были определены нач альные индексы (технические веса) критериев. Пусть ( acp ) v — среднее по v -му столбцу значение всех элементов, кроме макс имального (равного 1). Определим

Индексы критериев находим из условия
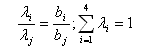
что позволяет получить:
| Критерий | SA | EF | EB | EC |
| лi | 0.261 | 0.254 | 0.317 | 0.168 |
Такой способ определения технических весов отражает стремление найти в области допустимых решений вершину с наилучшими значениями по всем критериям.
Затем проводилась оптимизация по глобальному критерию, что дало следующий результат:
SA =0,965; EF =0,85; EB =0,45; EC =0,675.
Для диалога с ЛПР значения по критериям ЕВ и ЕС были представлены в единицах стоимости. ЛПР предъявлялись: век- тор z 1 максимальных значений, достигаемых при максимиза ции по каждому из критериев по отдельности, и вектор y 1 зна чений критериев, достигаемых при оптимизации по глобально му критерию с приведенными выше индексами:
z 1 = {1; 1; -276; -157}; y 1 = {0,965; 0,85; -1920; -1269}.
Перед ЛПР был поставлен вопрос: все ли компоненты век- тора y 1 имеют удовлетворительные значения? При ответе на этот вопрос использовался вектор z 1, компоненты которого представляли собой максимально возможные (недостижимые одновременно) значения компонентов вектора у1 Руководитель определил значение по критерию ЕВ как наименее удовлетво рительное и нашел нижний уровень по критерию ЕВ: -1000.
Далее были найдены максимально возможные значения трех прочих критериев при ряде ограничений, дополнительно накладываемых на критерии ЕВ:
| EB | > -750 | > -1000 | > -1250 | > -1500 |
| SA | 0.67 | 0.78 | 0.84 | 0.9 |
| EF | 0.62 | 0.72 | 0.82 | 0.88 |
| EC | -731 | -157 | -57 | -157 |
При рассмотрении этой таблицы руководитель выбрал вектор при ЕВ > -1500 как обеспечивающий приемлемый ком промисс между повышением качества по критерию ЕВ и пони жением качества по критериям S А и EF . Для новой области допустимых решений (при ЕВ > -1500) приведенным выше способом были подсчитаны новые значения индексов для трех критериев:
| Критерий | SA | EF | EC |
| лi' | 0.885 | 0.775 | 0.910 |
Далее была проведена оптимизация по глобальному критерию с индексами. Полученное решение (вектор y 2) вместе с вектором z 2 максимальных значений критериев, достигаемых уже при новой области допустимых значений переменных,
z 2={0,9; 0,88; -157}, у2={0,885; 0,775; -1068},
было предъявлено ЛПР во время третьего диалога с ним. Руководитель определил значение по критерию ЕС как наименее удовлетворительное и выбрал в качестве нижнего уровня по EC значение —600.
Затем были определены максимально возможные значения двух критериев при ряде ограничений, накладываемых на ЕС:
| EC | > -800 | > -600 | > -400 |
| SA | 0.85 | 0.8 | 0.73 |
| EF | 0.8 | 0.75 | 0.68 |
На рис. 3.7 приведена блок-схема метода STEM .

Рис. 3.7. Блок-схема метода STEM
Руководитель выбрал вектор при ЕС > —800 как обеспечив ающий приемлемый компромисс между повышением качества по критерию ЕС и понижением качества по критериям SA и EF . Зная сильную взаимозависимость критериев SA и EF , он выбрал решение, соответствующее максимуму EF , как окончат ельное решение проблемы:
SA=0,76; EF=0,8; EB=-1500; EC=-800.
Выводы
- Предшественниками методов принятия решений во многих слу чаях являются методы исследования операций. С помощью методов исследования операций: а) разрабатываются модели, описывающие объективную реальность; б) определяется единственный критерий оптимальности решения; в) рассчитывается оптимальное решение.
- Существенное отличие проблем принятия решений от проблем исследования операций состоит в наличии многих критериев оценки качества решения. Компромисс между критериями мо жет быть найден только на основе предпочтений ЛПР.
- Существует особый класс задач принятия решений, в которых модели имеют объективный характер (как в задачах исследо вания операций), но качество решений оценивается по многим критериям. Эти задачи могут быть названы многокритериаль ными задачами с объективными моделями. Они находятся на границе между исследованием операций и принятием решений.
- Одним из первых многокритериальных методов является метод «стоимость-эффективность». Он включает в себя два этапа:
- построение моделей стоимости и эффективности;
- синтез оценок стоимости и эффективности. На втором этапе используются подходы:
- оптимизация по одному критерию при заданном ограничении по второму;
- построение множества Э-П.
- 5. Средством решения многокритериальных задач с объективными моделями являются человекомашинные процедуры (ЧМП). ЧМП представляют собой циклический процесс взаимодействия ЛПР и компьютера. Каждый шаг ЧМП состоит из фазы анализа, вы полняемой ЛПР, и (разы расчетов, выполняемой компьютером. Можно выделить три группы ЧМП: 1) прямые, основанные на выборе коэффициентов важности критериев; 2) ЧМП сравнения векторов; 3) ЧМП поиска удовлетворительных значений критериев. Одной из первых ЧМП является STEM , основанная на идее последовательного наложения ограничений на критерии.
| Нечего надеяться полностью избавиться от субъективности в задачах, связанных с выбором решений. Даже в простейших однокритериальных задачах она неизбежно присутствует, проявляясь хотя бы в выборе показателя эффективности и математической модели явления. Е.С . Вентцель. Исследование операций |
ВОЛШЕБНЫЕ СТРАНЫ
Обращение ректора Университета Власти к студентам
«Вы уже полгода занимаетесь в нашем единственном в мире Университете Власти . Надеюсь , вы уже заметили , что новое образование , которое вы получаете , стоит гораздо больше , чем вы платите за него .
От вас потребуются предельное напряжение внимания и упорный труд , но этого будет недостаточно . Мы хотим заручиться вашим согласием на прямое вторжение в глубины вашего сознания и интеллекта , в ваш внутренний мир . Вы не просто усвоите определенный набор знаний , но и научитесь умению распоряжаться этими знаниями , искусству быть лидером . Овладев этим искусством , вы сможете генерировать свежие идеи и увлекать ими , вести за собой людей . Не слепое повиновение , а сотрудничество и осознанная , широкая поддержка сделают вас истинными лидерами новой эпохи .
Теперь подробнее о самом процессе обучения . К каждому студенту прикреплен компьютерный учитель , который будет взаимодействовать с вами через обучающие программы , компьютерные учебники и книги ; он же будет присутствовать в обслуживающих вас роботах , в системе управления автомобилем . Словом , он будет рядом с вами на каждом шагу . Этот учитель будет изучать вас , подбирать задания , тренировать на многочисленных тестах – он будет учить вас учиться эффективно . Он сам будет находить пробелы в ваших знаниях и восполнять их новыми соответствующими заданиями , подбором новых книг и компьютерных программ для совершенствования умений . Он будет развивать в вас необходимые для руководителя черты характера , путешествуя с вами в виртуальных мирах и помогая в преодолении препятствий .
В процессе предварительного отбора студентов для нашего университета мы смогли убедиться , что у каждого студента есть хорошие задатки для того , чтобы стать лидером нового типа , каким мы его представляем , - образованным , инициативным , решительным , обладающим знанием , как вести себя в быстро изменяющемся и непростом мире , а также умением делать сложный выбор лучшего варианта решения при противоречивых и не до конца определенных оценках» .
( Продолжение следует )
Лекция 4. ОЦЕНКА МНОГОКРИТЕРИАЛЬНЫХ АЛЬТЕРНАТИВ: МНОГОКРИТЕРИАЛЬНАЯ ТЕОРИЯ ПОЛЕЗНОСТИ
1. Снова об этапах процесса принятия решений
- Различные группы задач принятия решений
- Пример
- Многокритериальная теория полезности ( MAUT )
- Основные этапы подхода MAUT
- Аксиоматическое обоснование
- Основные теоремы
- Построение однокритериальных функций полезности
- Проверка условий независимости
- Определение весовых коэффициентов (коэффициентов важности) критериев
- Определение полезности альтернатив
- Метод SMART – простой метод многокритериальной оценки
- Первый эвристический метод
- Веса критериев
- Как люди назначают веса критериев
- Практическое применение
- Выводы
- Библиографический список
Дата: 2019-02-19, просмотров: 443.