Вычисление молекулярных орбиталей, а с их помощью различных характеристик молекул - первоначальная цель любого квантовохимического расчета. Затем возникает не менее важная проблема химической трактовки результатов. Чтобы обеспечить решение последней задачи, рассмотрим, что представляют собой МО двухатомных молекул, составленных из элементов второго периода периодической таблицы.
Минимальный ЛКАО базис для расчета МО произвольной гомоядерной двухатомной молекулы состоит из 1s, 2s и 2р валентных атомных орбиталей, полное число которых равно десяти: по пять на каждый атом. Чтобы найти коэффициенты cim разложения МО по АО, необходимо решить секулярное уравнение десятого порядка. В результате будут получены 10 различных МО, заполнение которых определяется числом электронов в молекуле. Расчеты показывают, что в каждой МО гомоядерной двухатомной молекулы несколько коэффициентов велики (обычно два), остальные или равны нулю, или близки к нему. Для того чтобы АО входили в МО с большим вкладом, необходимо выполнение следующих условий: 1) энергии АО должны быть сравнимы по величине; 2) АО должны иметь отличное от нуля перекрывание, т. е. обладать одинаковыми свойствами симметрии относительно оси молекулы.
Пример. s-AO могут комбинировать с s-, px-функциями, если ось х системы координат и ось молекулы совпадают, но не с ру-, рz-АО (рис. 3.2): интеграл перекрывания s- и px -функций отличен от нуля, в то время как для s- и ру- и рz-АО функций он равен нулю.
Расчет основного состояния молекулы Li2 по методу Рутана в минимальном базисе ОСТ АО дает следующие в порядке возрастания энергии занятые МО (а и в обозначают ядра):
φ1 = 0.7048(1sa+1sb)+0.0095(2sa+2sb)+0.0003(2pxa+2pxb);
φ2 = 0.7054 (1sa-1sb)+0.0209(2sa-2sb)+0.0032(2pxa+2pxb); (3.2)
φ3 = - 0.1440(1sa+1sb)+0.5298(2sa+2sb)+0.1144(2pxa+2pxb).
Видно, что именно комбинация сходных АО дает наибольший вклад в МО. Отталкиваясь от этого факта, можно, не проводя точного расчета, рассмотреть основные качественные закономерности электронного строения двухатомных молекул первого периода.
Рассмотрим вначале классификацию и обозначения МО гомоядерных молекул. При этом принимаются во внимание:
1) симметрия МО относительно оси молекулы;
2) симметрия МО относительно плоскости, перпендикулярной оси молекулы;
3) тип АО, в которые переходят МО при увеличении межъядерного расстояния;
4) симметрия МО относительно центра инверсии молекулы.
МО, симметричные относительно отражения в плоскости молекулы, называют s -орбиталями, антисимметричные относительно такого отражения МО называют p -орбиталями.
МО двухатомных молекул характеризуются квантовым числом l , аналогичным квантовому числу m в атоме: l определяет величину проекции орбитального момента электрона на молекулярную ось. МО с l ¹ 0 являются дважды вырожденными, т. к. проекция момента на ось молекулы равна ± l h . Для s -МО l =0, для p -МО l =1. Аналогично, имеются МО с l =2, 3, ..., называемые, соответственно, d -, j -, …МО.
Далее, все МО характеризуются индексами g (gerade - четный) и u (ungerade - нечетный). Эти обозначения зависят от того, инвариантна МО (g) или меняет знак (u) при инверсии относительно центра симметрии. Четность и нечетность МО лежат в основе правил отбора разрешенных электронных переходов: возможны переходы u « g и невозможны переходы u « u и g « g.
Антисвязывающие (разрыхляющие) МО, к которым относятся МО, антисимметричные относительно плоскости, перпендикулярной оси молекулы, обозначают символом *: s *, p *, d * и т. д. МО определяется также типом АО, из которых она построена и в которые она переходит при увеличении межъядерного расстояния. Например, запись s ls означает, что данная s -МО построена из 1s-АО и переходит в них при Rab® ∞. Иногда полезно также знать, в какую АО переходит данная МО при слиянии ядер. Такое состояние молекулы называют состоянием объединенного атома.
Диаграмма, показывающая, в какие состояния объединенного и разъединенных атомов переходит данная МО при изменении межъядерного расстояния, называют корреляционной диаграммой. При ее построении необходимо учитывать правило непересечения Вигнера—Неймана: уровни одинаковой симметрии, например, s , p , … и g, u, не пересекаются.
Корреляционная диаграмма МО гомоядерной молекулы, построенная на основании точных теоретических расчетов энергии МО гомоядерных молекул в зависимости от межъядерного расстояния, показана на рис. 3.3.Эти расчеты в согласии с данными молекулярной спектроскопии дают следующий порядок энергий МО для двухатомных молекул, построенных из атомов первого и второго периодов:
σ g 1s< σ 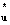 1s< σ g 2s< σ
1s< σ g 2s< σ 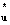 2s< π zu 2p= π yu 2p< σ g 2p< π
2s< π zu 2p= π yu 2p< σ g 2p< π  g 2p= π
g 2p= π 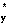 g 2p< σ
g 2p< σ 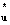 2s (3.3)
2s (3.3)
МО s g2p и вырожденные МО p z(y)u2p имеют близкие энергии и могут меняться местами в зависимости от конкретной молекулы.
Рис. 3.3. Корреляционная диаграмма МО гомоядерных двухатомных молекул
Абсолютные значения энергий МО для каждой молекулы разные, поэтому корреляционные диаграммы могут быть использованы только для качественных выводов, например, для анализа изменения орбитальной энергии при изменении межъядерного расстояния. Так, рис. 3.3 показывает, что энергия связывающих МО с уменьшением межъядерного расстояния повышается, в то время как энергия разрыхляющих орбиталей понижается. Кроме того, связывающие МО коррелируют с состоянием объединенного атома, имеющим то же квантовое число, что и данная МО. Разрыхляющие МО коррелируют с объединенным атомом, у которого квантовое число на одну или две единицы больше.
Подобно тому, как это имеет место атомах, существует классификация электронных термов гомоядерных двухатомных молекул. Одним из основных принципов классификации атомных термов была классификация по значениям полного орбитального момента. Очевидно, что в молекулах подобная классификация невозможна, так как поле ядер не обладает центральной симметрией и, следовательно, полный орбитальный момент может не сохраняться. Однако аксиальная симметрия поля ядер обусловливает сохранение проекции полного орбитального момента на ось молекулы, что позволяет классифицировать электронные термы по значениям этой проекции. Мы не будем останавливаться на этом вопросе подробно.
Дата: 2019-02-19, просмотров: 431.