В этом методе приближение НДП принимается для всех пар АО, кроме одних и тех же АО, принадлежащих одному атому. Матричные элементы опера-тора Фока имеют вид:
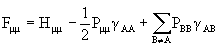 ,
, 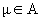
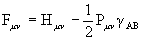
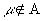 ,
, 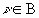
где РВВ =å Рm m (m Î В) – полная электронная заселенность валентных АО атома В.
Приближения, касающиеся одноэлектронных интегралов hm n , называемых остовными, состоят в следующем. Представим диагональные элементы hm m в виде:
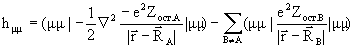 =
=
= 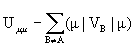 ,
, 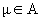
Um m можно рассматривать как энергию электрона на валентной орбитали c m свободного атома А. Интегралы (m ô VВô m )описывают электростатическое взаимодействие электрона, описываемого орбиталью c m , локализованной на атоме А, с атомным остовом В. Принимают, что взаимодействие любого электрона атома А с остовом В одинаково, т.е. (m ô VВô m )= VАВ: этот интеграл, в принципе, можно вычислить, задав вид АО. Однако на практике используют приближение Гепперт-Майер и Скляра, записывая
(m ô VВô m ) = 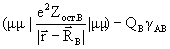 (2.53)
(2.53)
Первый член этой суммы называется интегралом проникновения: он описывает энергию кулоновского взаимодействия электрона, описываемого орбиталью c m , локализованной на атоме А, с нейтральным атомом В. Второй член описывает кулоновское взаимодействие заряда на атоме В QB = Zост, .В – РВВ с электронами на атоме А. Оказалось, что интегралы проникновения, как правило, малы по величине и ими можно пренебречь (это приближение не годится для систем с гетероатомами и при расчете оптических спектров). Тогда (m ô VВô m ) = VАВ » - QBg AB ( заметьте: VАВ ¹ VВА !). В итоге диагональные элементы оператора Фока в (2.51) можно переписать следующим образом:
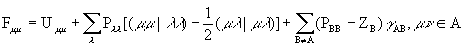 (2.54)
(2.54)
Обратимся теперь к недиагональным элементам оператора Фока. В приближении НДП интегралы hm n для m и n , центрованных на одном и том же атоме, равны нулю. Однако для орбиталей, центрованных на разных атомах, приближение НДП при вычислении hm n не применяется. Имея это в виду, запишем для этого случая:
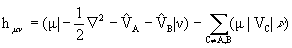 ,
, 
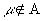 ,
, 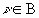 (2.55)
(2.55)
Последняя сумма включает члены, описывающие трехцентровые взаимодействия типа А-В-С: ими пренебрегают, а оставшийся член считают эмпирическим параметром. Он называется резонансным интегралом и обозначается b m n . В методе CNDO для него принимают следующее приближение:
hm n º b m n = b 0m n Sm n . (2.56)
Параметр b 0m n не зависит от типа взаимодействующих орбиталей, он характеризует лишь атомы А и В. Именно способами выбора этого параметра и отличаются различные варианты метода CNDO. С учетом (2.56) недиагональные элементы оператора Фока в (2.51) имеют вид
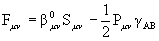 ,
, 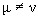 (2.57)
(2.57)
Подчеркнем, что требование обеспечить инвариантность метода достигается в CNDO путем сферического усреднения электронной плотности валентных АО. Природа АО (угловая зависимость) проявляется лишь в величинах Um m и Sm n .
Полная энергия молекулы в приближении CNDO записывается следующим образом:
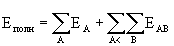 (2.58)
(2.58)
где одноатомные
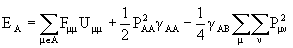 (2.59)
(2.59)
и двухатомные
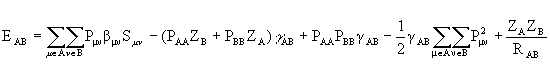 (2.60)
(2.60)
члены разделены.
Рассмотрим теперь на примере CNDO принципы параметризации полуэмпирических методов. Параметрами CNDO являются интегралы b m n , g AB ,Um m и VАВ , причем основным эмпирическим параметром, калибрующимся для воспроизведения определенных свойств молекул, является резонансный интеграл b m n = b АВ = b 0АВ SАВ . Параметры b 0АВ зависят только от типа соседних атомов А и В и определяются по формуле
b 0АВ=(1/2)k(b 0А + b 0В). (2.61)
Величины b 0А подбираются таким образом, чтобы в результате расчета методом CNDO воспроизводились разности орбитальных энергий e i- e j для основного состояния, а коэффициенты разложения МО по АО наилучшим образом совпадали с результатами неэмпирических расчетов в том же базисе (т.е. параметризуемым свойством является электронная плотность). Kоэффициент k равен 1 пар для s- и p-элементов и 0.75, если один атом из пары является d- элементом. Значения b 0А для атомов 2-го ряда периодической таблицы приведены в таблице 2.13.
Таблица 2.13 Значения 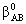 , используемые в методе CNDO.
, используемые в методе CNDO.
| Атом | H | Li | Be | B | C | N | O | F |
- 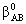 ,эВ ,эВ
| 9 | 9 | 13 | 17 | 21 | 25 | 31 | 39 |
Для оценки величин Um m используют выражения, описывающие удаление и присоединение электрона, связанного с орбиталью m :
Im = E+ -Е = - Um m -(Z ост. A-1)g AA
Am = -Um m -Z ост. Ag AA (2.62)
Здесь E+ и Е и E+ - энергии нейтрального и ионизированного атома, Im - потенциал ионизации, Am - сродство к электрону невозмущенной орбитали m . Чтобы иметь возможность описать одновременно удаление и присоединение электрона, проводят усреднение:
(1/2)(Im + Am ) = Um m + (Z ост. A –1/2)g AA (2.63)
и используют (2.63) для оценки Um m . Значения (1/2)(Im + Am ) для атомов 2-го ряда периодической таблицы приведены в таблице 2.14.
Таблица 2.14. Полусуммы потенциалов ионизации и сродства к электрону.
| Атом | H | Li | Be | B | C | N | O | F | ||||||||
| ½(IS+AS) | 7.176 | 3.106 | 5.946 | 9.594 | 14.051 | 19.316 | 25.390 | 32.272 | ||||||||
| ½(IP+AP) | - | 1.258 | 2.563 | 4.001 | 5.572 | 7.275 | 9.11 | 11.080 | ||||||||
Кулоновские интегралы g AB рассчитывают теоретически с помощью 2s-ОСТ по формуле (2.50). Интегралы VАВ оценивают с помощью соотношения
VАВ = Zост. В g AB . (2.64)
Приведенная параметризация весьма популярна и называется CNDO/2. Диагональные элементы оператора Фока в этой схеме имеют вид:
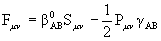 ,
, 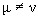 (2.65)
(2.65)
Недиагональные элементы описываются формулой (2.57).
Метод CNDO/2 дает хорошие значения геометрических характеристик молекул (длин связей, валентных углов), дипольных моментов, силовых постоянных, химических сдвигов ЯМР, барьеров внутреннего вращения. Чтобы распространить его на расчет спектров молекул, применяется иная параметризация, а метод называется CNDO/S (Дель Бене и Джаффе, 1968). За счет соответствующего подбора параметров этот метод эффективно учитывает электронную корреляцию. Резонансные интегралы разделяют на отдельные группы для s - и p -электронов и определяют по формуле (2.61), в которой коэффициент k для p -электронов берется равным 0,585, уменьшая тем самым вклад в энергию взаимодействия p -электронов с атомными остовами.. Одноцентровые кулоновские интегралы g AА находят по формуле Паризера-Парра:
g AА = Im - Am , (2.66)
где величины Im и Am определяют из спектроскопических данных для валентных состояний атомов. Двухцентровые интегралы g AB рассчитывают по формулам Матага-Нишимото:
g AB = (rm n + am n )-1 , am n = 2(g m m + g n n )-1 (2.67)
или Оно:
g AB = (r2m n + a2m n )-1/2 . (2.68)
Эти формулы были получены на основании того, что интегралы g AB должны зависеть от межатомных расстояний rm n так, чтобы удовлетворять граничным условиям
g m n = g m m rm n = 0
g m n ® е2/rm n rm n ® ¥ . (2.69)
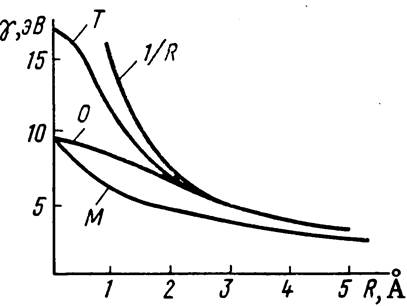 Последнее условие следует из того, что на больших расстояниях отталкивание двух распределенных электронных зарядов близко к отталкиванию точечных зарядов. Формулы (2.68) и (2.69) несколько занижают величину g AB по сравнению с теоретической оценкой (рис.2.6)
Последнее условие следует из того, что на больших расстояниях отталкивание двух распределенных электронных зарядов близко к отталкиванию точечных зарядов. Формулы (2.68) и (2.69) несколько занижают величину g AB по сравнению с теоретической оценкой (рис.2.6)
Результаты расчета спектральных характеристик молекул иллюстрирует таблица 2.15.
Таблица 2.15 Расчеты спектров методом CNDO/S.
| Соединение | Расчет | Эксперимент | Природа перехода |
| Энергия перехода Е, эВ | Энергия перехода Е, эВ | ||
| Бензол | 4.7 5.2 6.9 | 4.7 6.1 6.9 | π—π* π—π* π—π* |
| Пиридин | 4.3 4.8 5.4 7.1 | 4.3 4.8 6.2 7.0 | n—π* π—π* π—π* π—π* |
| Фуран | 5.2 5.8 7.3 | 5.9 6.5 7.4 | π—π* π—π* π—π* |
| Фурфурол | 3.2 4.9 5.7 | 3.5 4.6 6.2 | n—π* π—π* π—π* |
Дата: 2019-02-19, просмотров: 479.