В рамках приближения Борна-Оппенгеймера для анализа электронного поведения молекул достаточно рассматривать только электронное уравнение Шредингера (2.4) для выбранной ядерной конфигурации. Получить его точное решение для многоэлектронной молекулы, а тем более для кристалла невозможно и для этой цели используются приближения, введенные в квантовой химии атома, и прежде всего - метод Хартри-Фока.

В методе Хартри-Фока для молекул детерминант Слейтера (1.48), являющийся приближением к N-электронной волновой функции молекулы, составляется из занятых электронами молекулярных орбиталей (МО) j _i( x ):

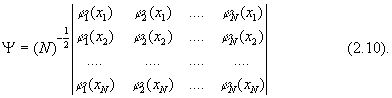
Каждая МО описывает поведение одного электрона в поле остальных электронов и (в отличие от атома!) всех ядер системы. Ясно, что концепция МО тесно связана с теорией многоэлектронного атома. Подобно АО, МО зависит от координат лишь одного электрона (является одноэлектронной) и записывается в виде произведения пространственной j _i(x) и спиновой h (s) компонент: j _i(x)= j _i(x)h (s). Каждая МО характеризуется своим значением энергии e _i, которая является собственным значением оператора Фока молекулы: электроны заполняют МО в порядке повышения энергии молекулы. Полная ХФ энергия молекулы с замкнутыми оболочками определяется соотношением, аналогичным выражению (1.55) в теории атома, а именно:

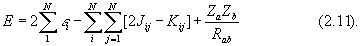
Последний член здесь описывает электростатическую энергию отталкивания ядер. Остальные члены имеют тот же смысл, что и в теории атома.

В минимизации энергии участвуют только занятые электронами МО, следовательно лишь они являются найденными физически обоснованно. Однако метод ХФ дает и характеристики свободных МО, которые соответствуют возбужденным энергетическим уровням молекулы лишь с большой ошибкой (около 100%). Такие МО называются виртуальными; применять их для трактовки спектроскопических данных следует с осторожностью – для этого существуют другие методы (см. ниже).

В дополнение к ХФ энергии, для оптимизации геометрии молекулы (если она известна лишь приближенно) и определения частот гармонических коле-баний ядер, вычисляются первые и вторые производные полной энергии относительно ядерных координат. Раньше производные рассчитывали методом конечных разностей; сейчас это делают непосредственным аналитическим дифференцированием выражения (2.11), что точнее. Минимум полной энергии соответствует наилучшей геометрии молекулы, а диагонализация матрицы вторых производных, являющихся силовыми постоянными молекулы, дает частоты нормальных колебаний. Кроме того, стационарные точки энергетической потенциальной поверхности (точки, где первые производные энергии по ядерным координатам обращаются в нуль) могут быть минимумом, максимумом или седловой точкой. Анализируя расположение и типы точек, можно охарактеризовать превращения молекул в ходе химических реакций. Мы вернемся далее к этой важной проблеме.

Полную сводку соответствующих аналитических формул можно найти в книге Y.Yamaguchi, Y.Osamura, J.D. Goddard, H.F.Schaffer III. A New Dimentions to Quantum Chemistry: Analytic Derivative Methods in Ab Initio Molecular Electronic Structure Theory. Oxford Univ.Press, N-Y, 1994. -471p.