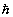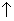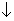До этого момента мы игнорировали тот факт, что электроны относятся к классу фермионов - частиц с полуцелым спином (собственным моментом количества движения). Спин электрона равен ± 1/2 (в единицах ). В квантовохимической литературе два возможных значения спина электрона a и b обозначаются символами и . Часто говорят "спин вверх" или "спин вниз", чтобы указать разные значения спина электрона. Чтобы учесть наличие спина, в аргумент одноэлектронных функций вводят спиновую переменную s, а функцию c _i (x_i) называют спин-орбиталью (x_i=r_i,s_i).

Из-за наличия спина имеются специальные ограничения на электронную волновую функцию, известные как принцип Паули.

1. Электронная волновая функция системы из нескольких электронов должна быть антисимметричной (менять знак) относительно обмена положениями и спинами пары из любых двух электронов i и j:

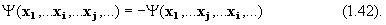
2. Никакие два электрона не могут быть в одном и том же квантовом состоянии (принцип исключения).

Чтобы понять, как нужно строить волновую функцию с учетом последнего обстоятельства, рассмотрим двухэлектронный атом гелия. Две эквивалентных волновых функции Хартри для этой системы имеют вид (1.24):

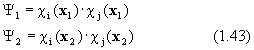
Очевидно, что ни одна из них не является антисимметричной. Однако легко заметить, что связанная с ними функция

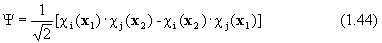
антисимметрична, 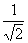– нормировочный коэффициент.

С математической точки зрения, вид этой волновый функции есть детерминант из спин-орбиталей c _i(х):

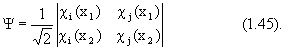
Если же мы попытаемся поместить электроны 1 и 2 на одну и ту же спин-орбиталь c _i, то получим:

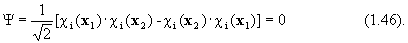
Значит волновая функция в виде (1. 44) удовлетворяет принципу исключения Паули.

Важным свойством детерминанта, известным из курса высшей математики, является то, что он меняет знак при перестановке двух любых его столбцов или строк; величина его при этом остается неизменной. Это как раз эквивалентно перемене мест двух электронов: электрон 1 перемещается с орбитали i на орбиталь j, а электрон 2 - с орбитали j на орбиталь i. Если же два столбца или две строки детерминанта одинаковы (что эквивалентно занятию двумя электронами одной и той же спин-орбитали), детерминант равен нулю.

Принцип Паули диктует, что две спин-орбитали с одинаковыми пространственными частями (т.е. с одинаковыми квантовыми числами n, l, m) отличаются только спиновыми компонентами. Пренебрегая малым по величине спин-орбитальным взаимодействием, каждую спин-орбиталь c_i(x) можно представить в виде произведения пространственной орбитали c_i(r) и спиновой функции h(s):c_i(x)=c_i(r)h(s).

На примере атома Не рассмотрим основное (синглетное) состояние. Из возможных вариантов распределения электронов между 1s и 2s – АО атома Не (рис. 7) этот описывается схемой а).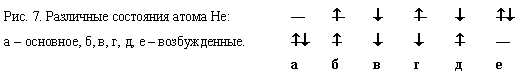

Электрон со спиновой функцией a обзначен стрелкой, направленной вверх, b - вниз.

Волновая функция основного состояния, выраженная через определитель, запишется так:

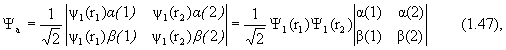
где функция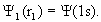

Y _a имеет симметричную пространственную часть и антисимметричную спиновую. Полный спин системы равен нулю, поэтому это состояние принято называть синглетным.

Заполнение орбиталей электронами происходит в порядке возрастания их энергий согласно принципу Паули и каждая не пустая АО может быть занята либо одним, либо двумя (но не более) электронами, причем в последнем случае электроны обязательно имеют противоположные спины и называются спаренными. АО с одинаковыми квантовыми числами n и l заполняются так, чтобы суммарный спин электронов был максимален (правило Хунда); другими словами сначала заполняется максимальное число АО с разными m.

Для нейтральных атомов в основном состоянии последовательность заполнения АО следующая:

1s < 2s < 2p < 3s < 3p < 4s ~ 3d < 4p < 5s ~ 4d < 5p < 6s ~5d ~ 4f < 6p < 7s < ...

Это ведет к так называемому aufbau-принципу, который служит обоснованием таблицы Менделеева. Следует подчеркнуть, что порядок заполнения орбиталей обусловлен не отношением их энергий, а требованием минимума полной энергии атома, которая отлична от суммы одноэлектронных энергий (см. выше). Здесь также играют роль спин-орбитальные и другие эффекты. Именно поэтому, в частности, 4s-AO заполняются электронами в атомах К и Ca раньше, чем 3d АО.

В итоге электроны с одним и тем же значением главного квантового числа n образуют электронные слои (оболочки). Эти слои, в свою очередь, построены из подоболочек, заполненных электронами с одинаковым значением орбитального квантового числа l. Слои с n=1,2,3, 4 ... обозначают буквами K, L, M, N,...

Детерминант Слейтера

Итак, представление многоэлектронной волновой функции в виде детерминанта обеспечивает ее правильные антисимметричные свойства. Кроме того, электроны неразличимы и их перестановка не должна менять свойства системы. Перестановка электронов для детерминанта эквивалентна перестановке местами столбцов (строк), что лишь меняет знак детерминанта. Поскольку волновая функция в принципе определена с точностью до фазового множителя, перемена знака свойств системы не меняет. Приближенная многоэлектронная волновая функция, построенная из ортонормированных спин-орбиталей отдельных электронов, называется детерминантом Слейтера:

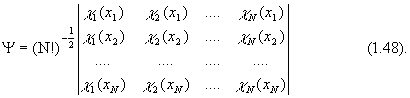
Детерминант Слейтера является единственной функцией, обеспечивающей антисимметричность волновой функции в орбитальном приближении. Следовательно, он дает только одно решение соответствующих одноэлектронных уравнений.

Хотя электроны неразличимы, в орбитальном приближении каждый электрон описывается "своей" волновой функцией. Системы, в которых все электроны спарены на орбиталях, называются системами с закрытыми (или замкнутыми) электронными оболочками. Для таких систем детерминант Слейтера состоит из дважды занятых электронами спин-орбиталей, число которых равно половине числа электронов. Системы с нечетным числом электронов называются системами с открытыми (незамкнутыми) оболочками.

Метод Хартри-Фока

Аппроксимация многоэлектронной волновой функции единственным детерминантом Слейтера (1.48) и использование приближения самосогласованного поля приводят к методу Хартри-Фока (ХФ). При этом исходное электронное уравнение Шредингера (1.20) путем довольно громоздких математических вычислений (см., например, М.Дьюар. Теория молекулярных орбиталей в органической химии) преобразуется в уравнения, где точный гамильтониан H (1.20) заменен оператором Фока (фокианом):

F = 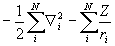+ 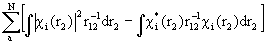(1.49)

(Здесь и далее мы используем принятую в квантовой химии атомную систему единиц: множитель 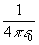опускается, m = 1, e = 1, 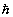=1. Введение атомных единиц делает формулы менее громоздкими).

Различие между F и H состоит в том, что оператор кулоновского межэлектронного взаимодействия 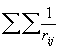заменен оператором в квадратных скобках, описывающим взаимодействие каждого электрона со средним полем всех остальных электронов с учетом требований принципа Паули. Из условия минимума энергии 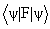возникает набор независимых уравнений для каждой одноэлектронной орбитали - уравнения Хартри-Фока:

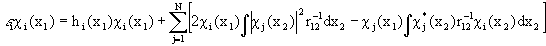1.50

Энергия электрона, находящегося на орбитали 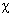_i, может быть получена умножением слева выражения (1.50) на 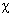_i и интегрированием по всему пространству:

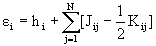(1.51),

где 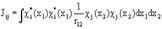, (1.52),

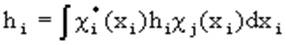(1.53),

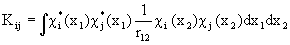. (1.54)

Одноэлектронный интеграл 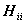описывает энергию электрона на орбитали 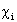в поле ядра без остальных электронов.

Двухэлектронный кулоновский интеграл 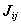описывает энергии межэлектронного отталкивания при независимом движении электронов.

Двухэлектронный обменный интеграл 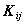отражает понижение энергии электронов с параллельными спинами на орбиталях 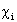и .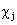

Полная энергия атома с замкнутыми оболочками (по 2 электрона на каждой орбитали) вычисляется в методе ХФ следующим образом:

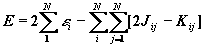(1.55)

Подчеркнем, что оператор Фока сам зависит от полного набора одноэлектронных волновых функций и его решение ищется самосогласованно. По этой причине метод ХФ иногда отождествляют с методом ССП. Поскольку, однако, общая стратегия самосогласования проявляется в квантовой химии во многих контекстах, название "метод Хартри-Фока" более точно.

Оператор Фока состоит из трех членов:

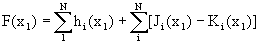(1.56)

Здесь h_i - точный одноэлектронный оператор (1.22):

h_i = - 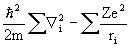(1.57)

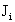- кулоновский оператор:

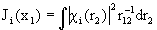(1.58)

и 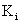- нелокальный обменный оператор:

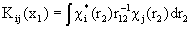(1.59)

Наличие обменного члена в методе ХФ эквивалентно введению поправки на корреляцию движения электронов, описываемых разными орбиталями. Другими словами, этим мы учитываем корреляцию между движением электронов с разными спинами (обменную корреляцию). Кулоновская корреляция, вызванная взаимным отталкиванием электронов, независимо от их спинов, в методе ХФ не учитывается: она является следствием приближения независимых частиц. Это - существенный недостаток метода и мы к нему еще вернемся. Кроме того, в противоположность точной волновой функции, однодетерминантная функция ХФ вследствие самосогласования не имеет сингулярности при |r_i - r_j|® 0, следующей из (1.6).

Уравнения ХФ могут, в принципе, быть решены численно любым стандартным методом решения интегро-дифференциальных уравнений (например, методом Монте Карло, методом сетки и др.).