Из-за наличия электрон-ядерного взаимодействия V_эя, пренебречь которым нельзя (см. таблицу 2.1), гамильтониан (2.2) не разделяется на ядерную и электронную части. Такое разделение может быть, однако, реализовано приближенно, если сделать зависимость электронной волновой функции y_эл от ядерной конфигурации R параметрической (приближение Борна-Оппенгеймера).
Для этого запишем молекулярную волновую функцию в виде произведения электронной и ядерной компонент Y({r, R}) = y_эл({r,R})y_яд({R}); заметим, что Y отлична от Y в (2.1). Соответствующее уравнение Шредингера имеет вид:

НY ({r, R})=ЕY ({r, R}), (2.3)

а электронная волновая функция удовлетворяет электронному уравнению Шредингера вида:

Н_{эy эл}= Е_{элy эл,} (2.4)

где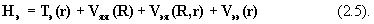

Рассмотрим теперь члены, описывающие кинетические энергии электронов и ядер:

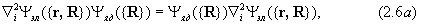
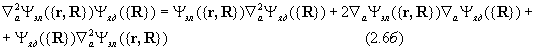
В жестких молекулах ядра лишь совершают малые колебания относительно равновесных положений, тогда как электроны делокализованы по всей молекуле. Это означает, что в стабильной молекуле y_эл является медленно меняющейся функцией ядерных координат R и ее первой и второй производной по этим координатам можно пренебречь. Отбрасывая соответствующие члены в (2.6 б) перепишем уравнение Шредингера (2.3) в виде:

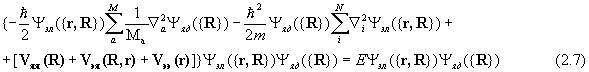
Примем теперь во внимание (2.4) и (2.5) и запишем:

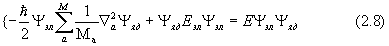
Деля это уравнение на y_эл , получаем уравнение для определения y_яд:

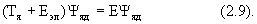
Таким образом, электронная энергия Е_эл, являющаяся суммой энергии движения электронов в поле фиксированных ядер и энергии ядерного взаимодействия, играет роль потенциальной энергии в уравнении Шредингера, описывающем движение ядер. Рассчитывая Е_эл для разных значений, получим потенциальную поверхность энергии, вдоль которой ядра движутся в энергетическом пространстве. Поэтому Е_эл называется адиабатическим потенциалом. Полная энергия молекулы в приближении Борна-Оппенгеймера есть сумма Е = Е_эл + Т_я, где Т_я есть колебательно-вращательная энергия ядер.

Обоснованность приближения Борна-Оппенгеймера обусловлена тем фактом, что отношение масс электрона и ядра не меньше, чем 1/1836. Поэтому движение ядерной подсистемы происходит много медленнее, чем электронной и для большинства задач ядерную конфигурацию можно считать фиксированной. Ядерная конфигурация, которая становится в принятом приближении вполне определенным понятием, стабильна относительно малых колебаний ядер. Она характеризует молекулярную структуру. Такая картина несправедлива, однако, если энергия ядерных колебаний ниже, чем разность энергий основного и возбужденных электронных состояний. При этом возникают так называемые вибронные состояния, а адиабатический потенциал теряет свой ясный физический смысл. Следствием этого является, в частности, важный структурный эффект Яна-Теллера, который будет рассмотрен позже.