Точное значение нормированной радиальной функции R_n,l для водородоподобного атома дается выражением:

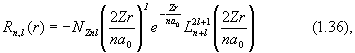
где 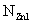- нормировочный множитель, зависящий от Z, n и l,

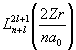- присоединенные полиномы Лягерра,

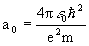- радиус Бора; a₀=0.529177·10^-10м, l= 0,1,2,3,..., .

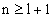Выражение (1.36) есть решение радиального уравнения Шредингера 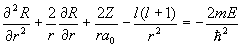, конкретный вид которого возник после разделения переменных в сферических координатах. Несколько первых полиномов Лягерра, описывающих основное (n = 1) и первые возбужденные (n = 2, n = 3) состояния, приведено в таблице 1.2, их зависимость от r изображена на рис. 1.2, 1.3.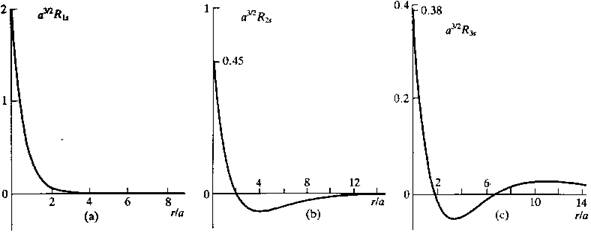

Рис.1.2. Радиальные составляющие 1s (a), 2 s (b), 3 s (c) орбиталей атома водорода.

Отметим некоторые свойства радиальных функций.

1) Как следствие свойств полиномов Лягерра, радиальные функции с различными n и l ортогональны.

2) Имеются точки (поверхности), где функции R_n,l (r) обращаются в нуль; они называются узловыми точками (поверхностями) или просто узлами. Вероятность найти электрон в узле равна нулю.

Таблица 1.2. Радиальные функции (нормированные функции R_n,l ( r ))

n	l	Rn,l ( r )
1	0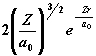
2	0 1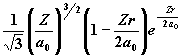
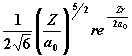
3	0 1 2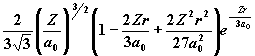

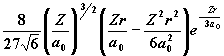
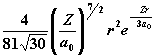
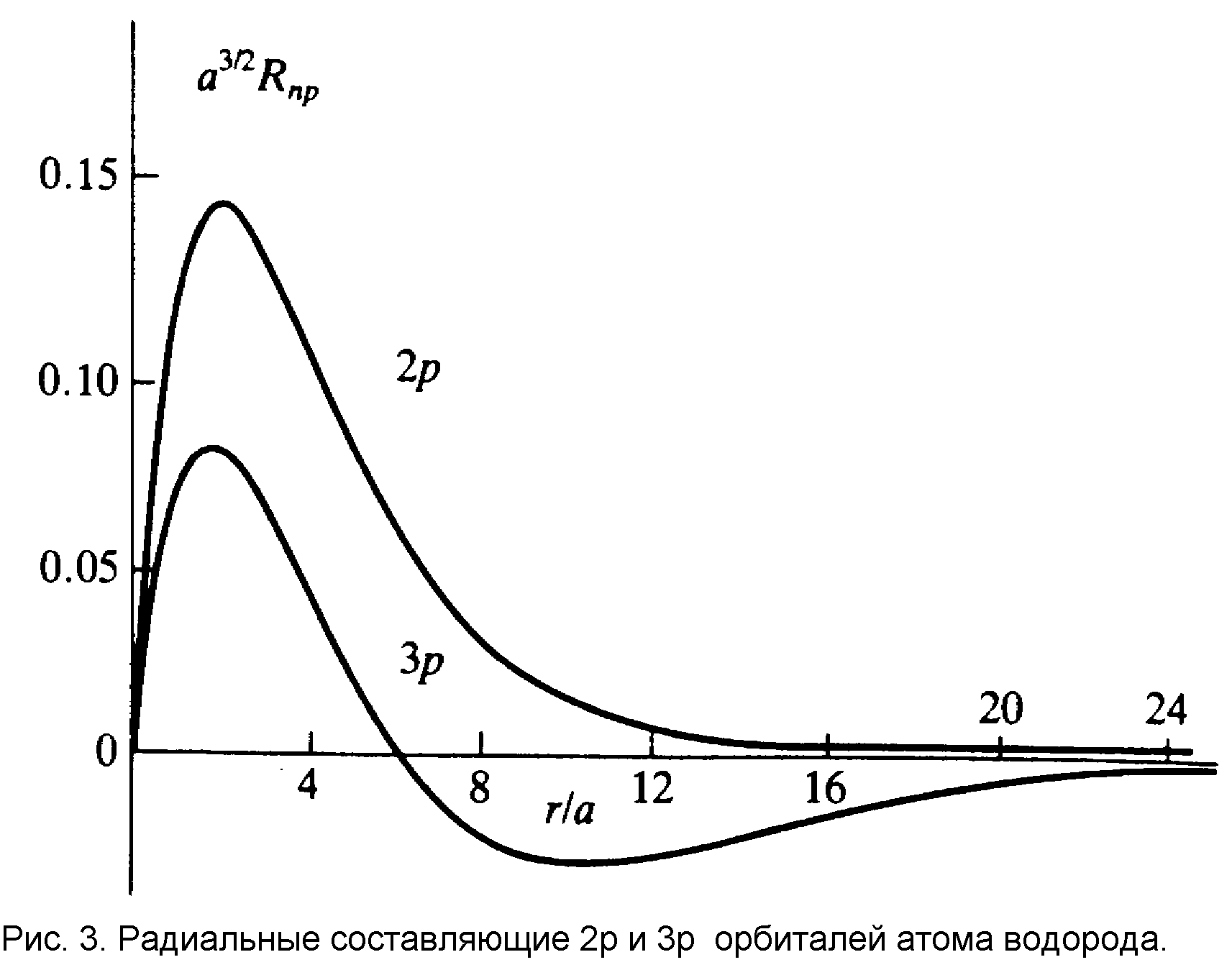
Радиальные функции с (n=1, l=0), (n=2, l=1), (n=3, l=2) и т.д. не имеют узловых точек; функции с (n=2, l=0), (n=3, l=1) и т.д. имеют одну узловую точку; функция с (n=3, l=0) – две узловые точки. Таким образом, число узлов радиальной функции равно (n-l-1).

3) Вероятность нахождения электрона в пространстве между значениями r и r+dr (слое) равна: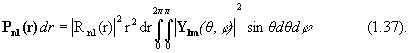

(из-за ортонормированности угловых функций - см. ниже - .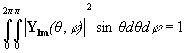

Функция P_nl (r), определяющая плотность вероятности нахождения электрона на расстоянии r от ядра, называется радиальной функцией распределения (см. рис.1.4)

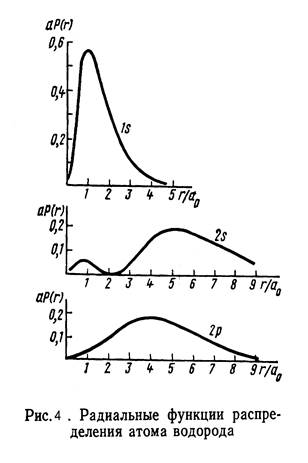Приравнивая нулю производную P_nl по r, можно найти наиболее вероятное положение электрона на соответствующей орбитали. Для основного состояния атома водорода оно равно радиусу Бора .

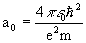4) Вблизи ядра электрон-ядерный потенциал (1.5) становится неопределенным из-за стремления знаменателя к нулю. Чтобы волновая функция на ядре была конечна и не равна нулю, необходимо, чтобы ее радиальная часть удовлетворяла асимптотическому условию

(¶ R/¶ r)| _{r® 0} = -(Z/a₀)R_{r® 0 .} (1.38)

5) На больших расстояниях от ядра атомная орбиталь зависит от r как

R ~ exp [ -(2I₁)^1/2 r], (1.39)

где I₁ - первый потенциал ионизации.

Угловые функции Y_lm (q , j ) - собственные функции оператора квадрата углового момента L² - описывают в сферических координатах (q , j ) угловую зависимость вероятности нахождения электронов в центральном поле атома. Они представляют собой сферические гармоники:

Y_lm(q, j) = (-1)^{(m+|m| )/2}{[(2l+1)/4p](1-| m| )! / (1+| m| )!}^1/2 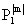(cosq)exp(imj) (1.40)

где l=0,1,2,..; m=-l, ...+l, 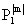(cosq ) - присоединенные полиномы Лежандра.

Это комплексные ортонормированные функции, из которых легко построить действительные комбинации, оставляющие АО собственными функциями того же одноэлектронного уравнения:

y_lm+ = (1/ 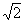)[Y_lm+ Y_l-m),

y_lm- = -(i/ 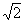)[Y_lm- Y_l-m), l=0,1,2, ... , m=0,1,2 , ... , l (1.41)

Таблица 1.3. Угловые части волновой функции атома, обладающего центральным полем.

l	m	ylm	Линейная комбинация	обозначение
0	0		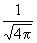-	s
1	0		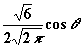-	pz
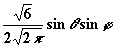
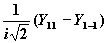
1	± 1			py
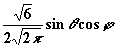
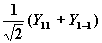
1	± 1			px
2	0		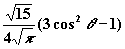-	dz2
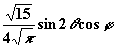
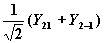
2	± 1			dxz
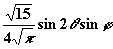
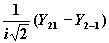
2	± 1			dyz
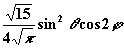
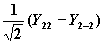
2	± 2			dx2-y2
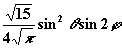
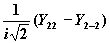
2	± 2			dxy

Как видно из таблицы 3 и рисунков 5 и 6, действительные угловые функции имеют простую интерпретацию в декартовых координатах. Для них, также как и для радиальных функций, характерно наличие узлов и узловых плоскостей.

При классификации электронных состояний атома придерживаются следующих представлений. Главное квантовое число n характеризует энергию орбитали. Орбитальное квантовое число l характеризует угловую зависимость орбитали (орбитальный момент). Для каждого l приняты свои обозначения (таблица 1.4 ).

Таблица 1.4. Обозначения орбиталей с различными угловыми зависимостями.

Важно понимать, что как результат приближения центрального поля угловая зависимость АО всех атомов одинакова!