Марковский анализ основан на понятии "состояния" (например, работоспособное и неработоспособное состояния) и перехода между этими состояниями во времени в предположении постоянной вероятности перехода. Стохастическую матрицу вероятностей перехода используют для описания переходов между состояниями и необходимых вычислений.
Для иллюстрации применения марковского анализа рассмотрим сложную систему, которая может находиться только в трех состояниях: работоспособном, ухудшенном и неработоспособном, обозначенных как состояния S1, S2, S3 соответственно. В любой момент времени система находится в одном из трех состояний. В таблице В.2 приведена вероятность того, что в следующий момент времени система будет находиться в состоянии Si, где i может быть 1, 2 или 3.
Таблица В.2 - Матрица Маркова
| Состояние в следующий момент времени | Состояние в текущий момент времени | ||
| S1 | S2 | S3 | |
| S1 | 0,95 | 0,30 | 0,2 |
| S2 | 0,04 | 0,65 | 0,6 |
| S3 | 0,01 | 0,05 | 0,2 |
Данный массив вероятностей называется матрицей Маркова или матрицей перехода. Следует отметить, что сумма в каждом столбце матрицы равна 1, т.к. это сумма вероятностей всех возможных состояний в каждом случае. Система также может быть представлена диаграммой Маркова, в которой круги отображают состояния, а стрелки - переходы с соответствующей вероятностью.
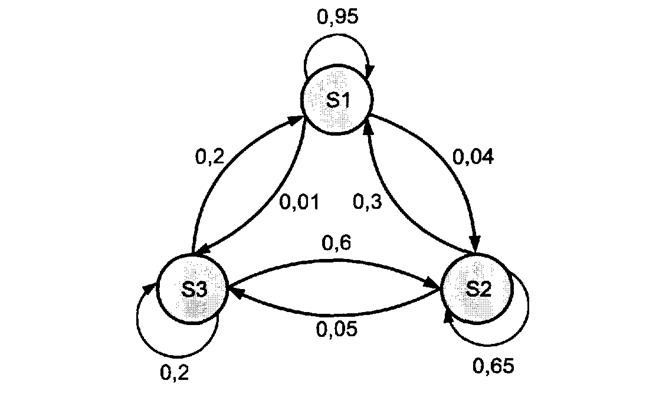 "Рисунок В.9. Пример диаграммы Маркова для системы"
"Рисунок В.9. Пример диаграммы Маркова для системы"
Стрелки, замкнутые на одном состоянии, обычно не показывают. В данном примере они приведены для полноты представления.
Если Pi - вероятность нахождения системы в состоянии i, для i = 1, 2, 3, то:
| Р1 = 0.95Р1 + 0.30Р2 + 0.20Р3. | (В.1) |
| Р2 = 0,04Р1 + 0.65Р2 + 0.60Р3. | (В.2) |
| РЗ = 0,01 Р1 + 0.05Р2 + 0.20Р3. | (В.3) |
Эти три уравнения зависимы, и система уравнений не может быть решена. Для решения необходимо одно из приведенных уравнений исключить, заменив его следующим уравнением.
| 1=Р1+Р2 + Р3. | (В.4) |
Полученные значения составляют 0,85, 0,13 и 0,02 соответственно для состояний 1, 2, 3. Система является полностью функционирующей в течение 85% времени, в ухудшенном состоянии в течение 13% времени и в состоянии отказа в течение 2% времени.
Рассмотрим ситуацию, когда система состоит из двух последовательных элементов, т.е. для работоспособности системы оба элемента должны находиться в работоспособном состоянии. Элементы могут быть в работоспособном состоянии или в состоянии отказа. Работоспособность системы зависит от состояния элементов.
Возможны следующие состояния элементов:
- состояние 1. Оба элемента находятся в работоспособном состоянии;
- состояние 2. Один элемент отказал и находится на восстановлении, а другой находится в работоспособном состоянии;
- состояние 3. Оба элемента отказали и находятся на восстановлении.
Если интенсивность отказа каждого элемента принять равной 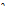 , а интенсивность восстановлений равной
, а интенсивность восстановлений равной  , и они являются постоянными, то диаграмму состояния перехода можно представить в следующем виде:
, и они являются постоянными, то диаграмму состояния перехода можно представить в следующем виде:
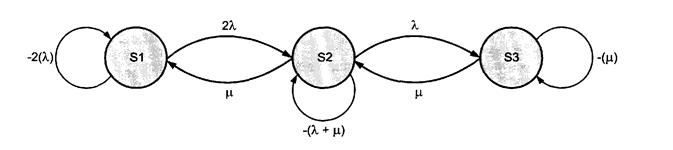 "Рисунок В.10. Пример диаграммы состояний перехода"
"Рисунок В.10. Пример диаграммы состояний перехода"
При этом интенсивность перехода из состояния 1 в состояние 2 равна 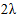 , поскольку отказ любого из двух элементов приводит систему в состояние 2.
, поскольку отказ любого из двух элементов приводит систему в состояние 2.
Пусть 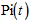 - вероятность нахождения системы в начальном состоянии i в момент времени t;
- вероятность нахождения системы в начальном состоянии i в момент времени t;
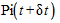 - вероятность нахождения системы в конечном состоянии в момент времени
- вероятность нахождения системы в конечном состоянии в момент времени 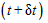 .
.
Тогда матрица переходов принимает следующий вид:
Таблица В.3 - Конечная матрица Маркова
| Конечное состояние | Начальное состояние | ||
| Р1(t) | P2(t) | Р3(t) | |

| 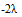
| М | 0 |

| 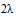
| 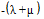
| 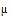
|

| 0 | 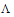
| 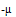
|
Необходимо отметить, что нулевые значения возникают потому, что переходы невозможны из состояния 1 в состояние 3 или из состояния 3 в состояние 1. Кроме того, сумма в колонке равна нулю при определении интенсивности.
В этом случае система уравнений имеет следующий вид:
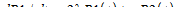 , ,
| (В.5) |
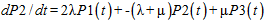 , ,
| (В.6) |
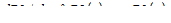 . .
| (В.7) |
Для простоты можно предположить, что требуемая работоспособность соответствует устойчивому состоянию системы.
Если 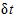 стремится к бесконечности,
стремится к бесконечности, 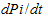 стремится к нулю, что позволяет упростить уравнения. Также необходимо использовать дополнительное уравнение (см. В.4). Тогда уравнение A(t) = P1(t) + P2(t) можно записать в виде:
стремится к нулю, что позволяет упростить уравнения. Также необходимо использовать дополнительное уравнение (см. В.4). Тогда уравнение A(t) = P1(t) + P2(t) можно записать в виде:
А = Р1 +Р2.
Следовательно, 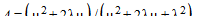 .
.
В.24.5 Выходные данные
Выходными данными марковского анализа являются вероятности пребывания системы в различных состояниях, а следовательно - оценки вероятностей отказа и/или безотказной работы существенных компонентов системы.
Дата: 2019-02-19, просмотров: 387.