Теория Байеса может быть применена различными способами. В данном примере рассмотрено построение таблицы Байеса для проведения медицинских исследований по определению наличия у пациента заболевания. До начала исследований предполагается, что у 99% населения этого заболевания нет, у 1% - заболевание есть (априорная информация). Достоверность теста такова, что если у человека имеется заболевание, то результаты тестов положительны в 98%. Если у человека заболевание отсутствует, результаты теста положительны в 10%. Ниже приведена таблица Байеса.
Таблица В.5 - Таблица Байеса
| Признак | Априорная вероятность | Условная вероятность правильности теста | Произведение вероятностей | Апостериорная вероятность |
| Есть заболевание | 0,01 | 0,98 | 0,0098 | 0,0901 |
| Нет заболевания | 0,99 | 0,10 | 0,0990 | 0,9099 |
| Сумма | 1 | 0,1088 | 1 |
Применяя теорему Байеса, произведение определяют умножением априорной вероятности на условную вероятность. Апостериорные вероятности определяют делением значения отдельного произведения на сумму произведений. Результаты расчета показывают, что в отношении положительного результата теста априорное значение возросло с 1% до 9%. Более того, велика вероятность того, что даже при положительном результате теста наличие заболевания маловероятно. Анализ уравнения (0,01 х 0,98)/((0,01 х 0,98) + (0,99 х 0,1) показывает, что положительный результат при отсутствии заболевания важен для апостериорных значений.
Рассмотрим следующую сеть Байеса:
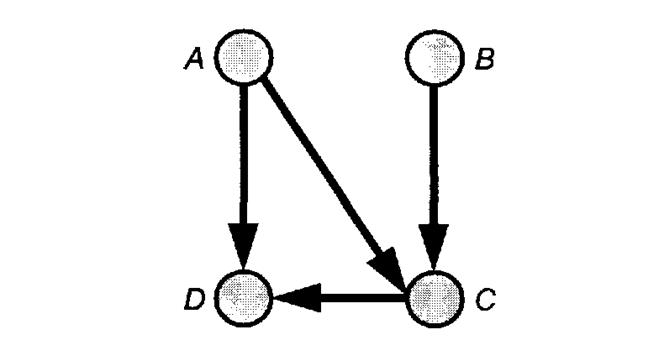 "Рисунок В.11. Пример сети Байеса"
"Рисунок В.11. Пример сети Байеса"
В соответствии с условными априорными вероятностями, определенными в нижеследующих таблицах, и обозначениями Y - положительный, а N - отрицательный, положительный результат указывает на наличие заболевания.
Таблица В.6 - Априорные вероятности для узлов А и В
| Р (А = Y) | Р (А = N) | Р (В = Y) | P(B = N) |
| 0,9 | 0,1 | 0,6 | 0,4 |
Таблица В.7 - Условные вероятности, определенные для узла С с узлами А и В
| А | В | Р (С = Y) | Р (С = N) |
| Y | Y | 0,5 | 0,5 |
| Y | N | 0,9 | 0,1 |
| N | Y | 0,2 | 0,8 |
| N | N | 0,7 | 0,3 |
Таблица В.8 - Условные вероятности, определенные для узла D с узлами А и С
| А | С | Р (D = Y) | P(D = N) |
| Y | Y | 0,6 | 0,4 |
| Y | N | 1,0 | 0,0 |
| N | Y | 0,2 | 0,8 |
| N | N | 0,6 | 0,4 |
Для определения апостериорной вероятности P( 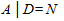 , С = Y) необходимо предварительно вычислить Р(А,
, С = Y) необходимо предварительно вычислить Р(А, 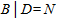 , C = Y).
, C = Y).
Используя правило Байеса, значение вероятности 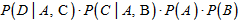 необходимо определить по формуле, как показано ниже в таблице, при этом в последней графе указаны нормализованные вероятности, сумма которых равна 1, как показано в предыдущем примере.
необходимо определить по формуле, как показано ниже в таблице, при этом в последней графе указаны нормализованные вероятности, сумма которых равна 1, как показано в предыдущем примере.
Таблица В.9 - Апостериорная вероятность для узлов А и В с узлами D и С
| А | В | Р (D = Y) | P (D = N) |
| Y | Y | 0,4 x 0,5 x 0,9 x 0,6 = 0,110 | 0,4 |
| Y | N | 0,4 x 0,9 x 0,9 x 0,4 = 0,130 | 0,48 |
| N | Y | 0,8 x 0,2 x 0,1 x 0,6 = 0,010 | 0,04 |
| N | N | 0,8 x 0,7 x 0,1 x 0,4 = 0,022 | 0,08 |
Для получения P( 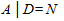 , С = Y) все значения В суммируют:
, С = Y) все значения В суммируют:
Таблица В.10 - Апостериорная вероятность для узла А с узлами D и С
P( 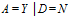 , C=Y) , C=Y)
| P( 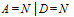 , C=Y) , C=Y)
|
| 0,88 | 0,12 |
Полученные результаты показывают, что априорная вероятность Р (A=N) увеличилась с 0,1 до 0,12 (апостериорные данные) и изменения являются незначительными. С другой стороны, значение вероятности P( 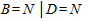 , C=Y) изменилось с 0,4 до 0,56. Это изменение уже более существенно.
, C=Y) изменилось с 0,4 до 0,56. Это изменение уже более существенно.
В.26.5 Выходные данные
Байесовский подход может быть применен в той же степени, что и классическая статистика, с получением широкого диапазона выходных данных, например при анализе данных для получения точечных оценок и доверительных интервалов. Сети Байеса используют для получения апостериорных распределений. Графические представления выходных данных обеспечивают простоту понимания модели, при этом данные могут быть легко изменены для исследования корреляции и чувствительности параметров.
Дата: 2019-02-19, просмотров: 393.