Преимуществами метода Монте-Карло являются следующие:

- Метод может быть адаптирован к любому распределению входных данных, включая эмпирические распределения, построенные на основе наблюдений за соответствующими системами.

- Модели относительно просты для работы и могут быть при необходимости расширены.

- Метод позволяет учесть любые воздействия и взаимосвязи, включая такие тонкие как условные зависимости.

- Для идентификации сильных и слабых влияний может быть применен анализ чувствительности.

- Модели являются понятными, а взаимосвязь между входами и выходами - прозрачной.

- Метод допускает применение эффективных моделей исследования многокомпонентных систем, таких как сеть Петри.

- Метод позволяет достичь требуемой точности результатов.

- Программное обеспечение метода доступно и относительно недорого.

Недостатки метода состоят в следующем:

- Точность решений зависит от количества итераций, которые могут быть выполнены (этот недостаток становится менее значимым с увеличением быстродействия компьютера).

- Метод предполагает, что неопределенность данных можно описать известным распределением.

- Большие и сложные модели могут представлять трудности для специалистов по моделированию и затруднять вовлечение заинтересованных сторон.

Метод не может адекватно моделировать события с очень высокой или очень низкой вероятностью появления, что ограничивает его применение при анализе риска.

В.25.7 Ссылочные стандарты

МЭК 61649 Критерии согласия, доверительные интервалы и нижние доверительные границы для распределения Вейбулла

Руководство ИСО/МЭК 98-3:2008 Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения

В.26 Байесовский анализ и Сеть Байеса

В.26.1 Краткий обзор

Создание байесовского анализа приписывают преподобному Томасу Байесу. Для оценки полной вероятности он предложил объединить априорные данные с апостериорными.

Общий вид теоремы Байеса:

,

где Р(Х) - вероятность события X;

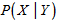 - вероятность события X при условии, что произошло событие Y;

Ei - i-e событие.

В самой простой форме теорему Байеса можно записать:

.

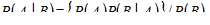Байесовский анализ отличается от классической статистики предположением, что параметры распределений являются не постоянными, а случайными переменными. Вероятность Байеса можно легко понять, если рассматривать ее как степень уверенности в определенном событии в противоположность классическому подходу, основанному на объективных свидетельствах. Поскольку подход Байеса основан на субъективной интерпретации вероятности, то он может быть полезен при выборе решения и разработке сетей Байеса (или сетей доверия).

Сеть Байеса представляет собой графическую модель, представляющую переменные и их вероятностные взаимосвязи. Сеть состоит из узлов, представляющих случайные переменные, и стрелок, связывающих родительский узел с дочерним узлом (родительский узел - переменная, которая непосредственно влияет на другую дочернюю переменную).

В.26.2 Область применения

Теории и сети Байеса широко применяют по причине их интуитивной понятности и благодаря наличию соответствующего программного обеспечения. Сети Байеса применяют в различных областях: медицинской диагностике, моделировании изображений, генетике, распознавании речи, экономике, исследовании космоса и в современных поисковых системах. Они могут находить применение в любой области, где требуется установление неизвестных переменных посредством использования структурных связей и данных. Сети Байеса могут быть применены для изучения причинных связей, углубления понимания проблемной области и прогнозирования последствий вмешательства в систему.

В.26.3 Входные данные

Входные данные для Байесовского анализа и сети Байеса подобны входным данным для модели Монте-Карло. Для сети Байеса основными этапами являются:

- определение переменных системы;

- определение причинных связей между переменными;

- определение условных и априорных вероятностей;

- добавление объективных свидетельств к сети;

- обновление доверительных оценок;

- определение апостериорных доверительных оценок.