Из рассмотренных выше теоретических положений взаимного пересечения многогранных поверхностей следует, что для построения проекций линии пересечения пирамиды ДАВС с призмой EKGU (рис. 88) необходимо выполнить следующее:
- построить проекции точек пересечения рёбер пирамиды с гранями призмы;
- построить проекции точек пересечения рёбер призмы с гранями пирамиды;
| Рис. 90 Рис. 91 |
- соединить попарно отрезками прямых одноимённые проекции точек пересечения ребер многогранников с гранями каждого из них, расположенных в одной и той же грани каждого из многогранников.
На чертеже проекции пирамиды и призмы расположены относительно друг друга таким образом, что происходит полное проницание призмы пирамидой. Это подтверждается взаимным расположением горизонтальных проекций геометрических фигур. В результате образуются две пространственные линии пересечения – линия входа и линия выхода.
Рассматривая расположение горизонтальных проекций рёбер пирамиды относительно горизонтально-проецирующих граней призмы, становится вполне очевидным, что с гранями последней пересекаются только рёбра ДВ, ДА и ДС боковой поверхности пирамиды. А так как грани призмы являются горизонтально-проецирующими, то с горизонтальными E1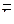 
1 
1K1, E1 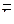1Ū1U1 и U1Ū1 
1G1 проекциями граней призмы совпадают горизонтальные 11, 21, 31, 41, 51 и 61 проекции точек пересечения рёбер ДВ, ДА и ДС пирамиды.
Фронтальные 12, 22, 32, 42, 52, 62 проекции точек (рис. 89) строят на основании принадлежности их соответственно рёбрам ДВ, ДА и ДС пирамиды, проведя в направлении фронтальных проекций рёбер линии связи. Фронтальная 22 проекция точки 2 пересечения ребра ДВ пирамиды с гранью E 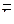K призмы является невидимой, так как фронтальная проекция этой грани призмы является невидимой. Проекцию 22 точки заключают в круглые скобки.
Далее (рис. 90) анализируют расположение рёбер прямой призмы относительно граней пирамиды. Из расположения горизонтальных проекций фигур относительно друг друга следует, что ребра K , G и UŪ призмы с поверхностью пирамиды вообще не пересекаются. Горизонтальные проекции этих рёбер находятся вне контура проекции пирамиды.
С гранями ДВС и ДВА боковой поверхности пирамиды пересекается только ребро E 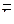призмы. А так как ребро E 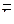призмы является горизонтально-проецирующей прямой, то с её E1 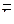1 проекцией совпадают проекции 71 и 81 точек пересечения последней соответственно с гранями ДВС и ДВА пирамиды.
При этом точка 7 принадлежит грани ДСВ, а точка 8 – грани ДВА пирамиды. Но горизонтальная Д1В1А1 проекция грани пирамиды на чертеже является невидимой, поэтому и горизонтальная 81 проекция точки, принадлежащей этой грани, тоже является невидимой и заключается в круглые скобки.
Построить фронтальные проекции точек 7 и 8, как принадлежащие проецирующему ребру E 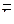призмы, невозможно. Но точки 7 и 8
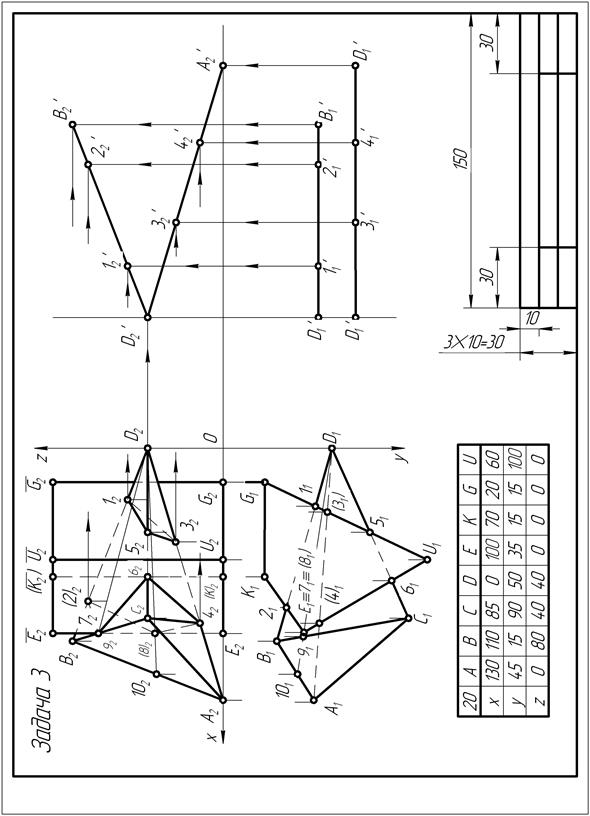
| Рис. 92 |
принадлежат одновременно граням ДВС и ДВА пирамиды. Поэтому построение фронтальных проекций этих точек выполняют на основании принадлежности последних граням пирамиды – плоскостям, заданным на чертеже треугольниками ДВС и ДВА (рис. 91).
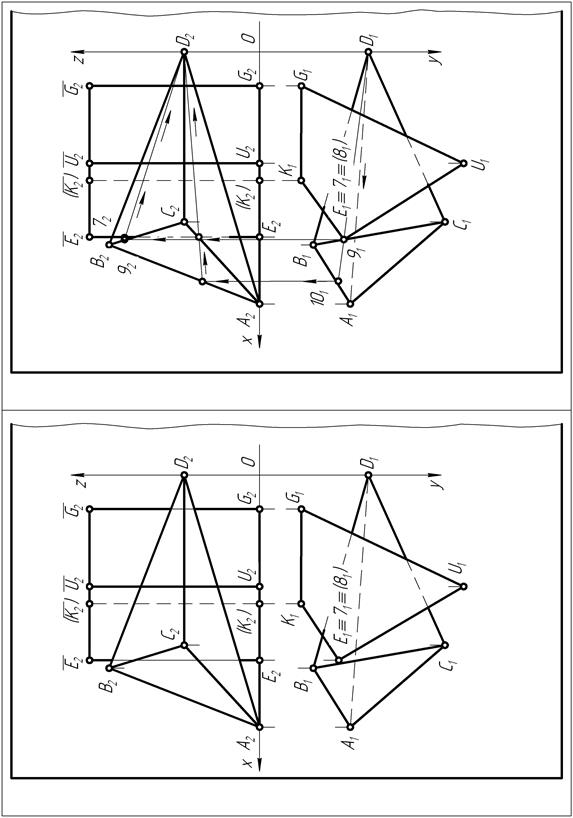
Известно, что точка принадлежит плоскости только в том случае, если она располагается на прямой, лежащей в этой плоскости. Поэтому, для построения фронтальных 72 и 82 проекций точек 7 и 8 на горизонтальной плоскости проекций через совпадающие проекции точек 7 и 8 и вершину Д пирамиды в каждой из граней проводят прямую линию. Она пересекает горизонтальную В1С1 проекцию стороны ВС треугольника основания пирамиды в точке 91 и горизонтальную В1А1 проекцию стороны АВ в точке 101. На основании принадлежности точки 9 стороне ВС и точки 10 стороне АВ строят фронтальные 92 и 102 проекции этих точек.
Соединив на фронтальной плоскости проекций точки 92 и 102 с точкой Д2 прямыми линиями, получают фронтальные 92Д2 и 102Д2 проекции прямых, на которых должны располагаться фронтальные 72 и 82 проекции принадлежащих этим прямым точек.
В том месте, где фронтальная Е2 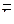2 проекция ребра призмы пересекает прямые 92Д2 и 102Д2, находятся искомые фронтальные 72 и 82 проекции точек пересечения горизонтально-проецирующего ребра E 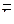призмы с гранями ДВС и ДВА пирамиды. При этом фронтальная 72 проекция точки 7 является видимой, а проекция 82 точки 8 – невидимой, так как принадлежит невидимой на плоскости П2 грани ДВА пирамиды. Проекцию 82 заключают в круглые скобки.
В результате выполненных построений определены положения на чертеже проекций точек пересечения ребра E 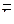призмы с гранями ДВС и ДВА пирамиды.
Теперь на фронтальной П2 плоскости проекций (рис. 92) отрезками прямых соединяют проекции точек пересечения рёбер пирамиды с гранями призмы и ребра E 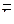призмы с гранями пирамиды. При этом следует помнить о том, что соединять можно только точки, лежащие в одной грани многогранника.
Прямые, расположенные на видимых проекциях граней, выполняются линиями видимого контура – сплошной толстой линией, а на невидимых проекциях граней – штриховой линией.
В результате получают горизонтальные и фронтальные проекции двух пространственных линий взаимного пересечения пирамиды ДАВС с прямой призмой EKGU.
После построения проекций линий пересечения многогранников приступают к окончательной обводке простым карандашом соответствующей твердости проекций заданных геометрических фигур с учётом их видимости на чертеже. При этом, сплошные толстые линии выполняют мягкими (М, 2М) карандашами, выдерживая толщину этих линий в пределах 0,8….1,2 мм. Штриховые линии выполняют карандашом средней (ТМ) твёрдости толщиной 0,4.....0,5 мм. Линии связи, оси проекций и линии дополнительных построений выполняют твёрдыми
(Т, 2Т) карандашами толщиной 0,2….0,3 мм.
Все буквенные и цифровые обозначения должны быть выполнены стандартным (ГОСТ 2.304-81) чертёжным шрифтом размера: 3,5; 5 или
7 мм.
Правую половину поля чертежа (рис. 92) оставляют свободной для последующих графических построений – определения натуральных величин рёбер основания и боковой поверхности пирамиды ДАВС, необходимых для решения задачи 4 [1].
На чертеже представлены графические построения определения натуральных величин рёбер ДВ и ДА пирамиды способом плоскопараллельного перемещения.
Дата: 2019-02-25, просмотров: 312.
