Построение исходного чертежа задачи выполняют на листе чертежной бумаги формата А3 (297´420 мм). На нем карандашом твердостью Т или 2Т тонкими линиями проводят рамки формата и чертежа, расположив длинную сторону формата горизонтально. В правом нижнем углу поля чертежа выполняют рамку основной надписи, а в левом нижнем углу – таблицу числовых значений размеров координат вершин А, В, С, Д, Е, К, G, U многогранников (рис. 84). В нее записывают числовые значения координат вершин соответствующего варианта задачи, взятые из табл. 3 «Методических указаний».

От линии, делящей длинную сторону формата пополам, на расстоянии (190 - Х_макс): 2 мм проводят тонкую вертикальную линию. На этой линии на расстоянии 105 мм от верхней рамки поля чертежа отмечают положение точки 0 – начало отсчета координат и проводят горизонтальную линию.

На вертикальной линии наносят обозначение оси проекций Х, а на вертикальной линии – вверх от точки 0 обозначение оси проекций Z, вниз от точки 0 – оси проекций Y.

В результате на поле чертежа в левой его половине получают прямоугольную систему осей проекций X, Y, и Z и приступают к построению горизонтальных и фронтальных проекций вершин трехгранной пирамиды ДАВС. Проекции вершин многогранников обозначают на чертеже кружками с диаметром просвета 1,5…2 мм, выполненными от руки или с помощью трафарета. Вначале строят горизонтальную Д₁ и фронтальную Д₂ проекции вершины Д пирамиды. А затем проекции вершин треугольника АВС – основания пирамиды.

Для этого на оси проекций Х влево от точки 0 откладывают в масштабе 1:1 числовое значение координаты соответствующей точки, например, Х_В и проводят линию связи, перпендикулярную оси проекций Х.

Вниз от оси проекций Х по линии связи откладывают числовое значение координаты Y_В той же точки. Получают горизонтальную В₁ проекцию точки В.

Вверх от оси проекций Х на линии связи откладывают числовое значение координаты Z_B. Получают фронтальную В₂ проекцию точки В. Попарно соединив (рис. 85) отрезками прямых одноимённые проекции точек

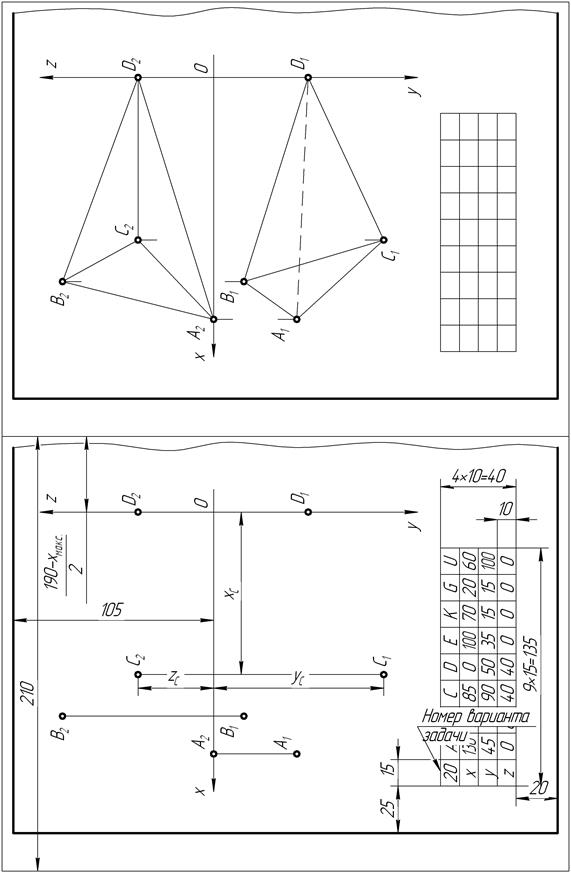
Рис. 84                                                                   Рис. 85

А, В и С, получают горизонтальную А₁В₁С₁ и фронтальную А₂В₂С₂ проекции основания пирамиды – треугольника АВС.

Тонкими линиями попарно соединяют одноимённые проекции вершин основания А, В, С с вершиной Д (Д_I, Д₂) пирамиды. Получают горизонтальную Д₁А₁В₁С₁ и фронтальную Д₂А₂В₂С₂ проекции трехгранной пирамиды ДАВС.

Анализируют видимость проекций ребер основания и боковой поверхности пирамиды отдельно для каждой из плоскостей проекций. При этом видимость проекций ребер и граней пирамиды на горизонтальной П₁ плоскости проекций определяют со стороны фронтальной П₂ плоскости проекций, а видимость фронтальных проекций – со стороны горизонтальной П₁ плоскости проекций.

На фронтальной плоскости проекций все ребра основания и боковой поверхности пирамиды являются видимыми. Их выполняют сплошными тонкими линиями. Проекции А₂В₂С₂, Д₂В₂С₂ и Д₂С₂А₂ граней пирамиды являются видимыми. Проекция Д₂В₂А₂ грани боковой поверхности пирамиды является невидимой, так как в пространстве эта грань пирамиды закрывается другими гранями пирамиды.

На горизонтальной плоскости проекций все ребра основания и боковой поверхности пирамиды, за исключением проекции ребра ДА, являются видимыми. Горизонтальная Д₁А₁ проекция ребра ДА располагается внутри контура проекции пирамиды. Видимость горизонтальной проекции ребра ДА легко устанавливается с помощью конкурирующих точек, принадлежащих ребру ВС и ребру ДА пирамиды. На основании этого проекция Д₁А₁ выполняется линией невидимого контура – штриховой линией.

Проекции Д₁В₁А₁ и Д₁А₁С₁ граней боковой поверхности пирамиды являются невидимыми, так как в пространстве они закрываются относительно горизонтальной плоскости проекций гранями ДВС и АВС.

Видимость на чертеже горизонтальных и фронтальных проекций ребер и граней пирамиды учитывается в последующих графических построениях. Это объясняется тем, что точки и прямые линии, расположенные на невидимых проекциях ребер и гранях пирамиды, являются невидимыми.

Аналогичным образом (рис. 86) строят на чертеже проекции четырехгранной прямой призмы ЕКGU, высотой 85 мм.

По отношению к горизонтальной плоскости проекций ребра боковой поверхности призмы являются проецирующими. Их горизонтальные Е₁, К₁, G₁, U₁ проекции представляют собой точки. Нижнее основание призмы располагается непосредственно в горизонтальной плоскости проекций, поэтому фронтальная проекция основания совпадает с осью проекций Х. Верхнее основание призмы располагается на высоте 85 мм от оси проекций Х. Разноименные проекции ребер боковой поверхности призмы расположены на соответствующих линиях связи. Попарно соединив отрезками

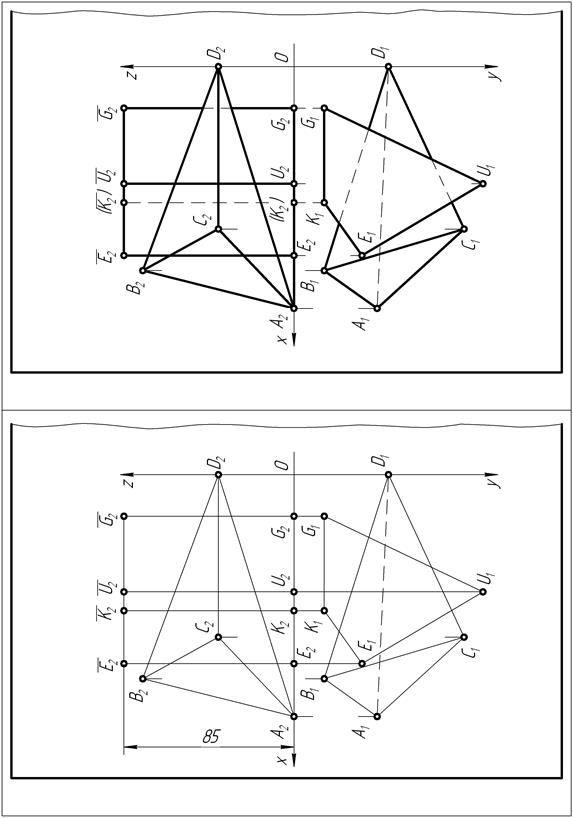
Рис. 86                                                                   Рис. 87

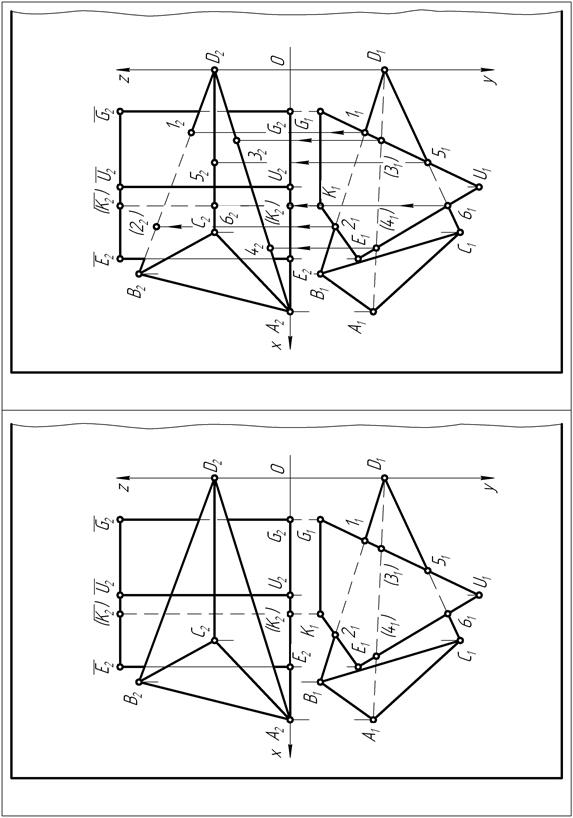
Рис. 88                                                                   Рис. 89

прямых одноименные проекции ребер боковой поверхности и вершины верхнего и нижнего оснований, получают горизонтальную и фронтальную проекции четырехгранной прямой призмы ЕКGU.

Грани боковой поверхности призмы расположены определенным образом по отношению к плоскостям проекций. Это обусловливает вполне конкретную видимость их проекций на чертеже. Так, по отношению к горизонтальной плоскости проекций, грани боковой поверхности призмы являются проецирующими. Поэтому горизонтальные проекции точек и прямых, принадлежащих этим граням, совпадут с горизонтальными проекциями граней призмы. 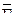Фронтальные Е₂Ē₂Ū₂U₂ и U₂Ū_{2 2}G₂ проекции граней являются видимыми, а проекции граней Е_{2 2 2}К₂ и К_{2 2 2}G₂ – невидимыми.

Производится корректировка видимости проекций отдельных элементов заданных геометрических фигур на чертеже (рис. 87), обусловленная их взаимным расположением относительно плоскостей проекций.

Так, на горизонтальной плоскости проекций ребра пирамиды, находящиеся внутри контура проекции призмы, выполняются штриховой линией. На фронтальной поверхности проекций проекция ребра U₂Ū₂ призмы является полностью видимой и выполняется сплошной линией, а проекция К_{2 2} – полностью невидимой и выполняется штриховой линией.

Часть проекции G_{2 2} ребра призмы, расположенная внутри контура проекции пирамиды, выполняется штриховой линией, так как ребро призмы расположено за гранями пирамиды по отношению к фронтальной плоскости проекций. Проекцию ребра Е 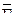 призмы, расположенного внутри контура горизонтальной проекции пирамиды, на фронтальной плоскости проекции следует предварительно выполнить тонкой линией.

Таким образом, в результате выполненных графических построений получают исходный чертеж задачи – фронтальную и горизонтальную проекции пирамиды ДАВС и призмы ЕКGU.