Определённые трудности в построении линий взаимного пересечения пирамидальных поверхностей обусловлены тем обстоятельством, что в подавляющем большинстве случаев грани и рёбра пирамид занимают в пространстве общие положения.

В значительной степени трудоёмкость решения задач на построение линий взаимного пересечения многогранных поверхностей уменьшается в том случае, когда одна из них представляет собой призматическую поверхность. Используя тот или иной способ преобразования проекционных чертежей, представляется возможным преобразовать грани призматической поверхности общего положения в проецирующие. В этом случае трудоемкость графических построений проекций линий пересечения пирамидальной и призматической поверхностей весьма значительно сокращается, так как в этом случае на чертеже уже имеется одна из проекций фигуры взаимного пересечения поверхностей.

На чертеже (рис. 75) представлены проекции пирамиды SABC и трехгранной призмы. Грани призмы представляют собой фронтально-проецирующие плоскости.

Из анализа взаимного расположения одноименных проекций многогранников относительно друг друга и относительно плоскостей проекций следует, что многогранники в пространстве пересекаются. Свидетельством тому является факт наложения друг на друга их одноименных проекций. При их пересечении происходит полное проницание, в результате чего должны образоваться две пространственные ломаные линии. Одна из них – линия входа, вторая – линия выхода.

Характер взаимного расположения фронтальных проекций многогранников относительно друг друга свидетельствует о том, что эти линии образуются при пересечении граней боковой поверхности пирамиды SABC с гранями I-II-III-I призмы и пересечения ребра III призмы с гранями SAC и SCB пирамиды. И так как грани трехгранной призмы представляют собой фронтально-проецирующие плоскости, то построение проекций линий взаимного пересечения многогранников, по сути дела, сводится лишь к построению недостающих проекций вершин пространственных многоугольников, представляющих собой проекции точек пересечения прямых SA, SB, SC пирамиды с гранями I-II, II-III, III-I призмы и ребра III призмы с гранями SAC и SCB пирамиды. Это обстоятельство предопределяет выполнение графических построений в следующей последовательности.

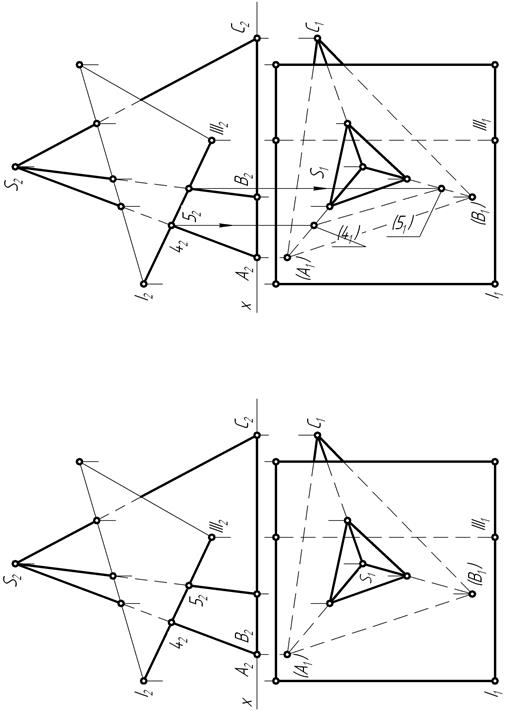
На фронтальной плоскости проекций (рис. 76) отмечают точки: 1₂, 2₂, 3₂ пересечения прямых S₂-A₂, S₂-В₂ и S₂-С₂ пирамиды с проекцией I₂-II₂ грани призмы.

На основании признака принадлежности точки прямой (рис. 77) строят их недостающие – горизонтальные  1₂, 2₂ и 3₂  проекции.

Попарно соединив прямыми (рис. 78) горизонтальные 2₁ и 3₁ проекции точек, лежащих в одной грани, получают проекции линии взаимного пересечения граней боковой поверхности пирамиды ABC с гранью I-II призмы.

Далее (рис. 79) на фронтальной плоскости проекций отмечают положения точек: 4₂ и 5₂ пересечения прямых S₂-A₂ и S₂-В₂ пирамиды с проекцией I₂-IΙI₂ грани призмы.

На основании признака принадлежности точек прямым SA и SB строят (рис. 80) их недостающие – горизонтальные 4₁ и 5₁ проекции. Соединив затем точки 4₁ и 5₁ штриховой линией (линией невидимого контура), получают горизонтальную проекцию линии взаимного пересечения грани SAB пирамиды с гранью I-III призмы.

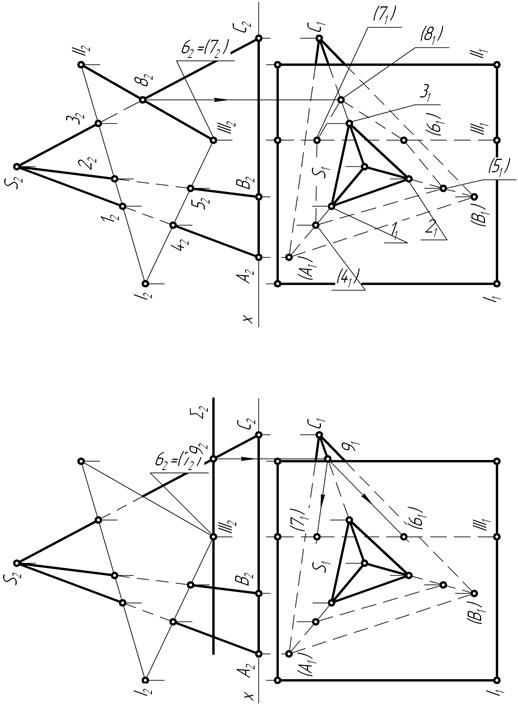
Затем строят проекции точек пересечения ребра III призмы с гранями SBC и SCA пирамиды (рис. 81).

Ребро III призмы является фронтально-проецирующей прямой и поэтому с ее фронтальной IΙI₂ проекцией совпадают проекции 6₂ и 7₂ точек пересечения этого ребра с гранями SBC и SCA пирамиды.

Для построения горизонтальных проекций точек 6 и 7 ребро III призмы заключают во вспомогательную горизонтальную секущую плоскость 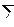 (сигма). В этом случае в сечении пирамиды SABC плоскостью  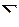образуется треугольник, стороны которого должны быть параллельны сторонам треугольника ABC основания пирамиды, лежащего в горизонтальной плоскости проекций. Соответственно и горизонтальные проекции сторон треугольника сечения должны быть параллельны горизонтальным проекциям сторон треугольника основания пирамиды.

В месте пересечения следа 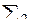 секущей плоскости с прямой S₂-С₂ отмечают точку 9₂ и строят её горизонтальную 9₁ проекцию. Затем на

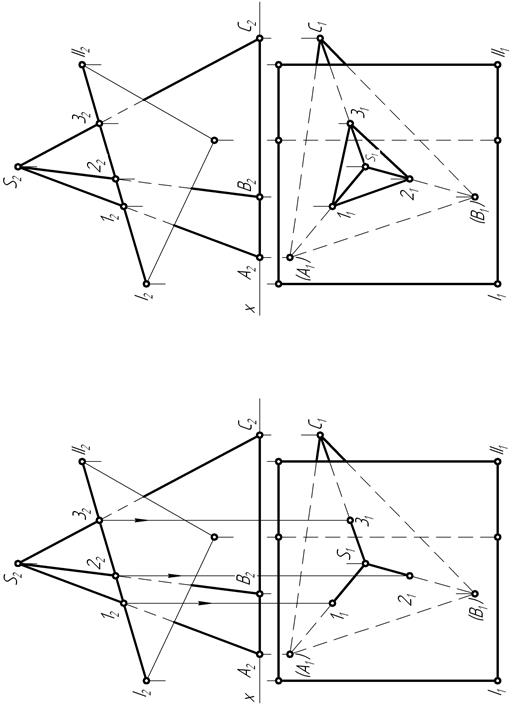
Рис. 77                                                                   Рис. 78

Рис. 79                                                                   Рис. 80

Рис. 81                                                                   Рис. 82

горизонтальной плоскости проекций из точки 9₁ проводят прямые, параллельные проекциям А₁-С₁ и С₁-В₁ сторон основания пирамиды, до пересечения с проекцией IΙI₁ ребра призмы.

В результате получают положения на чертеже проекций 6₁ и 7₁ точек пересечения ребра III призмы с гранями SBC и SCA пирамиды.

И, наконец, на фронтальной плоскости проекций (рис. 82) отмечают точку 8₂ пересечения прямой S₂-С₂ пирамиды с гранью IΙI₂-II₂ призмы. А затем на основании принадлежности точки 8 прямой SC строят ее горизонтальную 8₁ проекцию.

Теперь, попарно соединив линиями невидимого контура (штриховыми линиями) проекции точек 4, 5, 6, 7, и 4, лежащих в одних и тех же гранях пирамиды или призмы, получают проекции второй линии пересечения пирамиды с призмой – линию входа пирамиды SABC в призму.

Таким образом, наличие проецирующих граней у одного из многогранников весьма существенно снижает трудоемкость графических построений линий взаимного пересечения двух многогранных поверхностей.

На рис. 83 представлена аксонометрическая проекция (прямоугольная диметрия) полного проницания рассмотренных выше пирамидальной и призматической поверхностей.

Вопросы для самопроверки

1. Каким образом в общем случае решается задача на построение линии взаимного пересечения многогранных поверхностей?

2. Какие геометрические фигуры представляют собой в общем случае линии взаимного пересечения многогранных поверхностей?

3. Какое пересечение многогранных поверхностей называют полным и неполным проницанием?

4. Назовите количество и вид линий взаимного пересечения многогранных поверхностей при полном проницании.

5. Назовите количество и вид линий взаимного пересечения многогранных поверхностей при неполном проницании.

6. Где располагаются на чертеже проекции линий взаимного пересечения двух многогранников?

7. Пересекает ли ребро одного из многогранников поверхность другого, если проекция этого ребра пересекают контуры наложений проекций многогранников?

8. С чего начинают построения проекций линий взаимного пересечения пирамидальной и призматической поверхностей?

9. Каким образом можно сократить трудоемкость графических построений линий взаимного пересечения пирамидальной и призматической поверхностей, занимающих общие положения?

1.7. Последовательность выполнения построений графического решения задачи 3 [ 1 ]

Задача – построить линию пересечения пирамиды с прямой призмой.