Категорическими высказываниями
Между элементарными категорическими высказываниями устанавливаются следующие отношения.
1. Отношение противоречия (контрадикторности). Это отношение существует между высказываниями A – O, E – I. Высказывания, находящиеся в этом отношении, не могут быть одновременно ни истинными, ни ложными. Из истинности одного высказывания следует ложность другого, из ложности одного — истинность другого.
2. Отношение противоположности (контрарности). Это отношение существует между высказываниями А – Е. Противоположные высказывания не могут быть одновременно истинными, но могут быть одновременно ложными. Из истинности одного из них следует ложность другого, но из ложности одного из них может следовать как истинность, так и ложность другого.
3. Отношение частичной совместимости (субконтрарности): Это отношение устанавливается между высказываниями I – O. Субконтрарные высказывания не могут быть одновременно ложными, но могут быть одновременно истинными. Из ложности одного высказываия следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого высказывания.
4. Отношение подчинения. Это отношение существует между высказываниями A – I и E – O. Из истинности общих высказываний следует истинность частных высказываний подчиненных им, но из истинности подчиненного высказывания истинность общего не следует, оно может быть истинным, но может быть ложным. Указанная здесь неопределенность возникает в связи с трактовкой слова «некоторые» в традиционной логике. Обращаем внимание: это слово понимается в смысле «некоторые, а может быть все…».
Далее, из ложности подчиненного высказывания следует ложность подчиняющего высказывания, но из ложности подчиняющего высказывания ложность подчиненного с необходимостью не следует, оно может быть истинным, но может быть ложным. Причина неопределенности та же, что и выше.
Обращаем внимание на то, что данные отношения устанавливаются исключительно между сравнимыми по смыслу высказываниями, т. е. такими, у которых совпадают субъекты и предикаты соответственно, а отличаются они между собой показателем количества или связкой. Например, между высказываниями
«Некоторые американцы — любители жевательной резинки»
и
«Ни один американец не является любителем жевательной резинки»
существует отношение противоречия. Но между высказываниями
«Некоторые девушки любят сладкое»
и
«Некоторые девушки любят мороженое»
ни одно из вышеуказанных отношений установить нельзя, поскольку в этой паре высказываний различные предикаты — «любитель сладкого» и «любитель мороженого».
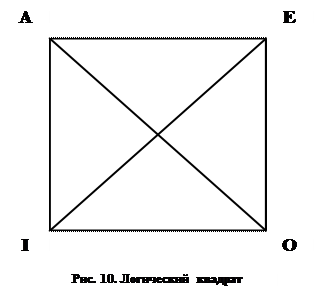
Рассмотренные выше отношения могут быть представлены наглядно с помощью схемы, именуемой «логическим квадратом» (Рис. 10).
Верхняя сторона квадрата соответствует отношению противоположности. Обе диагонали квадрата изображают отношение противоречия. Отношение субконтрарности отражается нижней стороной квадрата. Две вертикальные стороны квадрата изображают подчинение.
Сложные высказывания
Наш разговор о высказываниях завершим рассмотрением сложных высказываний.
Def Сложным называют высказывание, состоящее из двух или более простых высказываний, соединенных с помощью логических союзов.
Сложные высказывания можно понимать по аналогии со сложными предложениями: мы объединяем простые предложения в сложные с помощью грамматических союзов. Следует, однако, отметить, что логические союзы нельзя, однако, отождествлять с союзами грамматическими. Логические союзы — это своеобразные функции, которые определяют значение сложного предложения в зависимости от значения простых предложений, его составляющих.
Можно было бы построить много функций, представляющих логические союзы, но мы ограничимся указанием тех из них, которые наиболее часто используются в логике. Для их представления воспользуемся таблицами.
Пусть А и В — произвольные высказывания.
 |
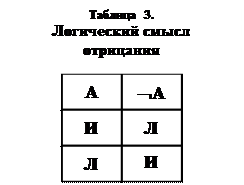Начнем с союза, который будем обозначать так: «Ø»[9]. Он называется «отрицание». Запись «ØА» читается «неверно, что А» или «не-А». Логический смысл этого союза заключается в том, что он переводит всякое истинное высказывание в ложное, а всякое ложное — в истинное (табл. 3).
Следующий логический союз «&» — конъюнкция. В естественном языке ему чаще всего соответствует грамматический союз «и». Запись «А&В» читается как «А и В». Логический смысл конъюнкции приведен в таблице 4.
 |
Как видно из таблицы 4 конъюнкция считается истинной, только в том случае, когда истинны оба члена конъюнкции. Примером конъюнкции может служить высказывание:
«Лиса — это хищное животное, и медведь больше лисы»[10].
Заметим также, что конъюнкции в естественном языке соответствует не только союз «и». Она может быть выражена с помощью других союзов. Например:
«Лондон — столица Великобритании, а Мадрид — столица Испании».
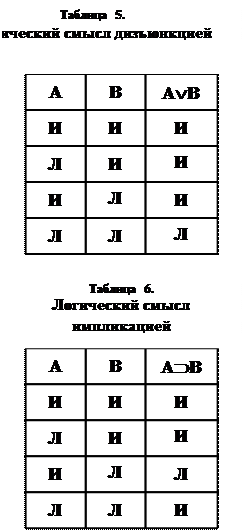
Символом «Ú» мы обозначаем логический союз, называемый «дизъюнкцией» или «простой дизъюнкцией». Запись «АÚВ» читается, как «А или В». Таким образом, логической дизъюнкции соответствует грамматический союз «или». Важно, что здесь «или» не носит исключающего характера, как это часто бывает в естественном языке. Указанная особенность находит свое отражение в таблице для дизъюнкции (табл. 5).
Примером дизъюнкции может служить следующее предложение.
«Здесь близко река или здесь близко озеро».
По-видимому, чтобы мы посчитали это предложение истинным, достаточно обнаружить хотя бы один из указанных водоёмов; но если их окажется два (и река и озеро), то вряд ли мы сочтем себя обманутыми. Именно такой смысл имеет дизъюнкция.
Для логического союза, именуемого импликацией, мы выберем символ «É». Выражение «АÉВ» будем читать «если А, то В»[11]. Смысл импликации представлен в таблице 6.
 |
Важно помнить, что речевой оборот «если…, то…» в логике не обязательно отражает причинно-следственную связь. Лучше понимать его как «если [условие], то [следствие]».
Примером такого употребления союза «если, то» является высказывание:
«Если книга имеется в магазине, то она имеется и в библиотеке».
Действительно, книгу можно обнаружить в библиотеке не по причине наличия ее в магазине, но при этом условии. Обращаем внимание на то, что две последние строки таблицы для импликации представляют известное логическое правило: «Из ложного высказывания, следует какое угодно высказывание».
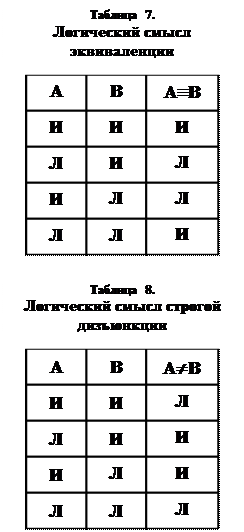
Следующий логический союз называется «эквиваленция». Для него мы выбрали обозначение «º». Этому логическому союзу в естественном языке соответствует речевой оборот «...тогда и только тогда, когда...». Поэтому запись «АºВ» договоримся читать «А тогда и только тогда, когда В»[12]. Эквиваленция определена следующей таблицей 7.
 |
Примерами эквиваленции могут служить такие высказывания:
«Прямоугольник является квадратом, тогда и только тогда, когда его стороны равны»
или
«Число делится на 10, если и только если оно делится на 5 и на 2»[13].
Наконец, последний логический союз, с которым мы познакомимся, называется «строгая дизъюнкция». В отличие от ранее рассмотренной дизъюнкции, этот логический союз используется для выражения несовместимости двух высказываний. Это отражается в таблице 8.
Запись «А¹В» условимся читать «либо А, либо В, но не то и другое вместе». Примером строгой дизъюнкции может служить высказывание:
«Либо эта шахматная фигура является белой, либо эта шахматная фигура является черной».
Резюме. Важнейшим элементом информации является высказывание. В языкознании высказыванию соответствуют повествовательные предложения. В традиционной логике высказыванию приписывают одно из двух значений: либо «истина», либо «ложь». Среди высказываний выделяют простые (элементарные) и сложные. Считается, что элементарное высказывание имеет структуру «субъект – связка – предикат», и различаются по количественным и качественным характеристикам. Сложные высказывания образуются из простых с помощью логических союзов.
Дата: 2019-02-25, просмотров: 313.
