Определение. Моментом k-го порядка называется выражение, вычисляемое по формулам:

а) для дискретной случайной величины:

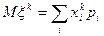, (6.3.1)

б) для непрерывной случайной величины:

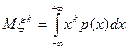. (6.3.2)

Для существования момента k-ого порядка необходимо:

а) для дискретной случайной величины — абсолютная сходимость ряда

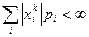, (6.3.3)

б) для непрерывной случайной величины — абсолютная сходимость интеграла

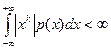. (6.3.4)

Поскольку 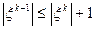, то из существования момента к-го порядка вытекает существование момента (к-1)-го порядка и, следовательно, всех моментов меньших порядков.

Определение. Момент k-го порядка величины 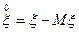 называется центральным моментом k-го порядка.

Особую роль играет второй центральный момент, который называется дисперсией и обозначается .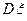

Определение. Дисперсией случайной величины 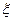 называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания:

. (6.3.5)

Свойства дисперсии.

1. Дисперсия постоянной величины равна нулю, т.е.

. n

2. Дисперсия является неотрицательной величиной, т.е. .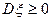

3. Для любых действительных чисел  и 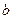 справедливо равенство

.

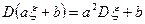Доказательство. Из свойства 2 математического ожидания получаем:

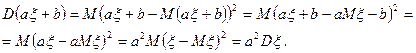
n

4. .

Доказательство. Используя определение дисперсии и свойства 2 и 3 математического ожидания, получаем:

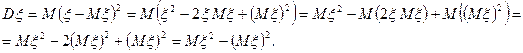
n

5. Если 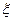 и  независимые случайные величины, дисперсия суммы случайных величин равна сумме дисперсий случайных величин, т.е.

.

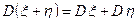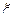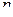Доказательство. Если  и  независимые случайные величины, то и случайные величины  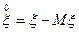и 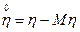 будут независимыми. Тогда, используя свойства 2-4 математического ожидания, получаем:

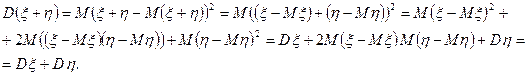
n

Очевидно, что дисперсия 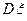 имеет размерность квадрата случайной величины 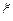. Для практических же целей удобно иметь числовую характеристику, размерность которой совпадает с размерностью .

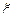Определение. Средним квадратичным отклонением случайной величины ξ называется выражение, вычисляемое по формуле:

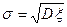. (6.3.6)

Пример 12. Найти дисперсию случайной величины 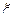, плотность которой имеет вид (равномерно распределенной на отрезке ):

m Решение. Используя определение дисперсии 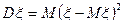, формулу для вычисления дисперсии непрерывной случайной величины (6.3.2) и результат примера 4, получаем:

.l

Пример 13. Найти дисперсию случайной величины 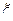, распределенной по нормальному закону с параметрами  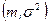(см. Пример 4).

m Решение. Используя определение дисперсии , формулу для вычисления дисперсии непрерывной случайной величины (6.3.2) и результат примера 5, получаем:

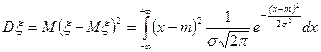. (6.3.5)

Делаем замену 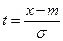 или 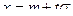, при этом 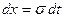. В этом случае выражение (6.3.5) примет вид:

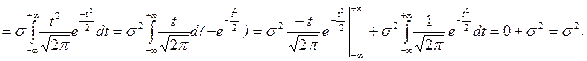 l

Пример 14. При условии примера 11 найти дисперсию случайной величины .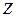

m Решение. Рассмотрим 1 способ нахождения дисперсии, используя ряд распределения случайной величины 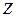, найденный в примере 12,

и свойство 4 дисперсии, получим:

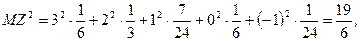
Напомним, что математическое ожидание 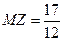 было найдено в примере 12.

Перейдем ко второму способу нахождения математического ожидания случайной величины . Используя свойство 5 дисперсии случайной величины, получим:

, ,

, ,

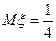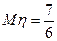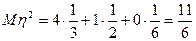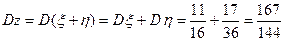, . l