Формула Бернулли
Определение. Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два исхода, и вероятности исходов остаются неизменными для всех испытаний.
Обычно эти две вероятности обозначаются через 
и 
, исход с вероятностью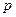 
называют «успехом» и обозначают символом 1, а второй – «неудачей» и обозначают символом 0. Очевидно, что и должны быть неотрицательными и должно выполняться равенство
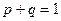. (4.1.1)
Пространство элементарных исходов каждого отдельного испытания состоит из двух исходов 1 и 0. Очевидно, пространство элементарных исходов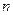 
испытаний Бернулли содержит 
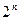последовательностей из 
символов 1 и 0. Так как испытания независимы, то вероятности перемножаются, т. е. вероятность любой конкретной последовательности есть произведение, полученное при замене символов 1 и 0 вероятности на и соответственно. Таким образом, вероятность исхода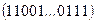 
равна:
.
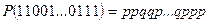Но на практике нас, как правило, интересует не порядок появления успехов в последовательности испытаний Бернулли, а их общее число.
Теорема. Вероятность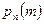 
того, что в испытаниях Бернулли число успехов равно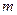 
, вычисляется по формуле
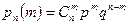, (4.1.2)
где — вероятность «успеха», а — вероятность «неудачи».
Доказательство. Событие «в испытаниях Бернулли число успехов равно 
и число неудач — 
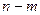» содержит столько элементарных исходов, сколько существует способов размещения символов на местах, т.е. 
. А так как вероятность конкретной последовательности, содержащей символов 1, равна 
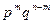, то в итоге получаем:
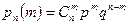. n
Число успехов в испытаниях обозначают через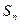 
, тогда 
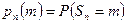. Очевидно, что 
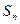есть случайная величина, а функция (4.1.2) является «распределением» этой случайной величины. Будем называть это распределение биномиальным. Слово биномиальное отражает тот факт, что (4.1.2) представляет собой m-й член биноминального разложения 
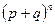. Отсюда следует, что
.
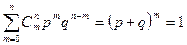Пример 1. Стрелок попадает в мишень с вероятностью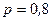 
. Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает:
a) ровно четыре раза;
б) не менее трех раз.
m Решение. Для решения данной задачи применим формулу (4.1.2), в которой:
.
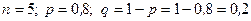а) Число успехов равно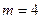 
. Таким образом, искомая вероятность:
.
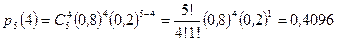б) Обозначим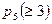 
— вероятность попадания не менее трех раз из пяти.
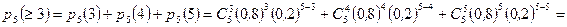
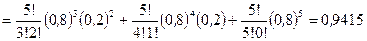. l
Пример 2. Сколько испытаний с вероятностью успеха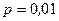 
нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5?
m Решение. Рассмотрим следующие события:
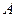— в схеме Бернулли наблюдался хотя бы один успех;
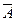— в схеме Бернулли не наблюдалось ни одного успеха.
Для решения задачи используем формулу (4.1.2), согласно которой вероятность того, что успехов не будет (т.е. число успехов равно нулю), равна:
.
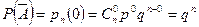Используя свойство вероятности противоположного события, получаем, что вероятность того, что будет хотя бы один успех, равна:
.
Остается найти наименьшее целое , для которого выполнено неравенство:
.
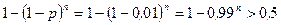Решим последнее неравенство.
.
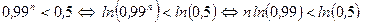Разделив последнее неравенство на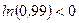 
, получим
.
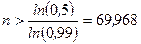Наименьшим целым числом 
, удовлетворяющим последнему неравенству, является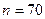 
. l
Пример 3. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен):
а) три партии из четырех или пять из восьми;
б) не менее трех партий из четырех или не менее пяти партий из восьми.
m Решение. Так как противники равносильны и ничейный исход партии исключен, то вероятности выигрыша и проигрыша каждой партии одинаковы и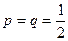 
.
а) Вероятность выигрыша трех партий из четырех равна:
,
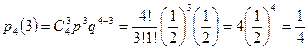а вероятность выигрыша пяти партий из восьми равна:
.
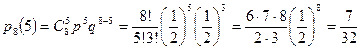Так как 
, то вероятнее выиграть три партии из четырех.
б) Вероятность выигрыша не менее трех партий из четырех равна:
а вероятность выигрыша не менее пяти партий из восьми равна:
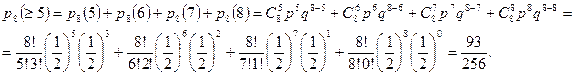
Так как 
, то вероятнее выиграть не менее пяти партий из восьми. l
Формула Пуассона
При больших значениях числа испытаний применение формулы Бернулли (4.1.2) затруднительно. Поэтому применяются простые, но достаточно точные приближенные формулы для вычисления 
. Пусть число испытаний достаточно «велико», вероятность «успеха» 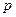достаточно «мала». Пусть произведение
(4.2.1)
и не мало, и не велико. В таких случаях удобно использовать для вероятности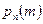 
предложенное Пуассоном приближение (формула Пуассона), которое мы сейчас выведем. По формуле Бернулли (4.1.2)
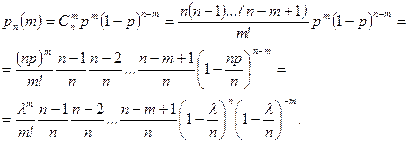(4.2.2)
При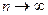 
и сделанных выше допущениях очевидны следующие приближения:
, 
.
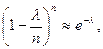
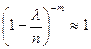Следовательно, (4.2.2) примет вид:
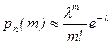, (4.2.3)
а это и есть формула Пуассона.
Замечание. При выводе формулы Пуассона (4.2.3) использовалось то, чт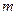о 
мало.
Замечание. Формула Пуассона (4.2.3) зависит от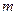 
и 
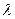. Значения функции (4.2.2) можно определить следующими способами:
§ можно воспользоваться Приложением 1;
§ используя функцию ПУАССОН(x;среднее;интегральная) из EXCEL; в которой аргумент x равен числу «успехов» 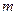, аргумент «среднее» равен 
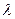, аргумент «интегральная» должен равняться 0;
§ используя функцию dpois(k, l) из MATHCAD, в которой 
и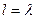 
.
Пример 4. Найти вероятность того, что среди 1460 человек ровно трое родились 29 февраля.
m Решение. Вероятность того, что один конкретный человек родился 29 февраля, равна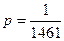 
, т.к. 29 февраля бывает ровно 1 раз в 4 года.
Далее находим коэффициент :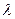
.
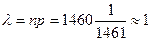Применяя (4.2.2), получаем:
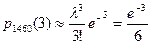. l
Пример 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность того, что при 5000 выстрелах в цель попало не менее двух выстрелов.
m Решение. Рассмотрим два противоположных события:
— при 5000 выстрелах в цель попало не менее двух выстрелов;
— при 5000 выстрелах в цель попало менее двух выстрелов.
Найдем вероятность события :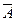
.
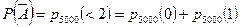В рассматриваемом примере
.
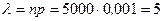Используя формулу Пуассона, получим
.
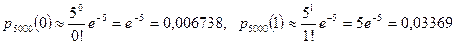Используя свойство вероятности противоположного события, получим
. l
Формулы Муавра – Лапласа
Если в схеме Бернулли ,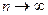 
, 
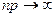, (4.3.1)
то следует применять формулы Муавра – Лапласа: локальную или интегральную.
Локальная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли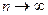 
, то для всех 
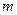справедлива локальная формула Муавра‑Лапласа:
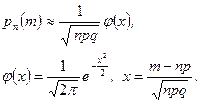(4.3.2)
Значения функции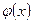 
, которую называют плотностью нормального распределения с параметрами 
, можно найти одним из следующих способов:
§ можно воспользоваться Приложением 2;
§ используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 0.
§ используя функцию dnorm(x, mu, sigma) из MATHCAD, в которо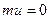й 
и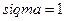 
.
Очевидно, что функция 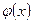является четной. Поэтому при определении 
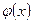для отрицательных 
нужно воспользоваться равенством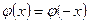 
.
Интегральная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли число испытаний 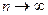, то для вероятности 
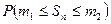того, что число успехов 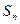заключено в пределах от 
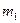до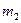 
, справедлива интегральная теорема Муавра‑Лапласа:
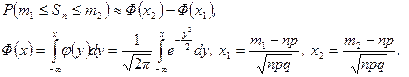(4.3.3)
Функция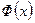 
, определенная формулой (4.3.3), называется функцией распределения нормального распределения с параметрами . Значения функции 
можно найти одним из следующих способов:
§ можно воспользоваться Приложением 3;
§ используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 1.
§ используя функцию pnorm(x, mu, sigma)из MATHCAD, в которо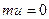й 
и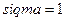 
.
Функцию при отрицательных значениях переменной можно определить по формуле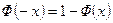 
.
Замечание. Наряду с функцией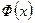 
используют функцию
. (4.3.4)
Для нее справедливо равенство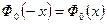 
; она связана с функцией 
равенством
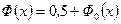. (4.3.5)
Пример 6. Симметричную монету бросают 400 раз. Определить вероятность появления герба:
а) от 185 до 210 раз;
б) ровно 200 раз;
в) не менее 200 раз.
m Решение. Для решения задачи применим локальную и интегральную теоремы Муавра‑Лапласа, для которых
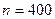, т.к. монету подбрасывали 400 раз, 
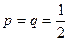, т.к. монета симметрична.
а) Используя интегральную теорему Муавра‑Лапласа, получим
б) Используя локальную теорему Муавра‑Лапласа, получим
;
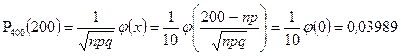в) Используя интегральную теорему Муавра‑Лапласа, получим
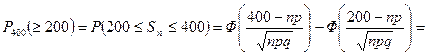
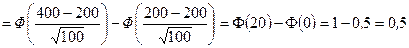. l
Пример 7. Команда состоит из 10 отличных и 15 хороших стрелков. Каждый стрелок производит по своей мишени 5 независимых выстрелов. Отличный стрелок при каждом выстреле попадает в цель с вероятностью 0,9, хороший — с вероятностью 0,8. Определить вероятность того, что общее число попаданий будет не менее 110.
m Решение. Найдем вероятность попадания при одном выстреле для произвольного стрелка. Для этого воспользуемся формулой полной вероятности. Пусть искомое событие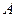 
— мишень поражена одним стрелком. Рассмотрим следующие гипотезы:
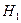— стреляет отличный стрелок;
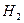— стреляет хороший стрелок.
Очевидно, что:
, 
, 
, 
.
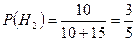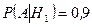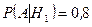Отсюда получаем:
, 
.
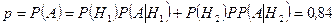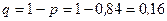Заметим, что общее число выстрелов
.
Теперь найдем вероятность 
того, что при 125 выстрелах число попаданий будет не менее 110. Для этого применим интегральную теорему Муавра‑Лапласа:
, 
,
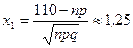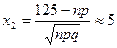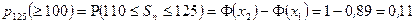. l
Пример 8. Вероятность попадания в мишень при одном выстреле 
. Найти наименьшее число выстрелов, которое надо произвести по мишени, чтобы с вероятностью 0,95 число попаданий было не менее 70.
m Решение. По условию задачи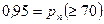 
. Для вычисления 
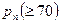применим интегральную теорему Муавра – Лапласа:
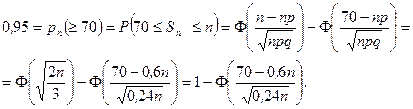
Заметим, что мы использовали то, что при больших значениях 
.
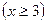
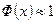Далее получаем
.
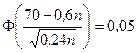Используя Приложение 3 находим, что
.
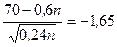Решая последнее уравнение для натуральных значений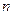 
, получаем, что n=132 . l
Дата: 2019-02-25, просмотров: 227.
