1. Математическое ожидание постоянной равно самой этой постоянной, т.е.
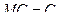 , где
, где 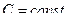 .
.
Доказательство. Постоянную 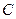 можно рассматривать как случайную величину, принимающую только одно значение
можно рассматривать как случайную величину, принимающую только одно значение 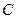 с вероятностью 1. Следовательно,
с вероятностью 1. Следовательно,
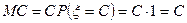 . n
. n
2. 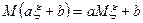 .
.
Доказательство. Пусть 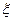 — непрерывная случайная величина. Тогда для случайной величины
— непрерывная случайная величина. Тогда для случайной величины 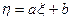 по формуле (6.2.4.) получаем:
по формуле (6.2.4.) получаем:

Аналогично доказывается и для дискретной случайной величины. n
3. Для любых случайных величин 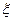 и
и  математическое ожидание их суммы случайных величин равно сумме их математических ожиданий, т.е.
математическое ожидание их суммы случайных величин равно сумме их математических ожиданий, т.е.
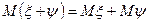 .
.
Доказательство. Пусть случайные величины 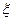 и
и  — дискретные. Случайная величина
— дискретные. Случайная величина 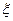 принимает значения
принимает значения 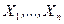 , а случайная величина
, а случайная величина  принимает значения
принимает значения 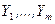 . Рассмотрим случайную величину
. Рассмотрим случайную величину 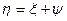
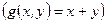 . Случайная величина
. Случайная величина 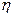 принимает значения
принимает значения  с вероятностями
с вероятностями 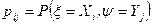 . Тогда:
. Тогда:
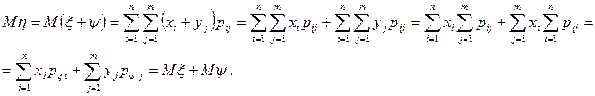
При доказательстве воспользовались тем, что
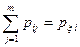 и
и 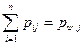 .
.
Действительно, учитывая, что
 ,
,
то
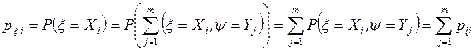 ,
,
аналогично доказывается, что
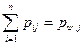 .
.
Аналогично доказывается и для непрерывной случайной величины. n
4. Если 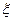 и
и  независимые случайные величины, то математическое ожидание произведения случайных величин равно произведению их математических ожиданий, т.е.
независимые случайные величины, то математическое ожидание произведения случайных величин равно произведению их математических ожиданий, т.е.
 .
.
Доказательство. Пусть величины 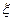 и
и  — дискретные. В силу независимости случайных величин имеет место равенство:
— дискретные. В силу независимости случайных величин имеет место равенство:
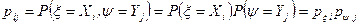 . Тогда
. Тогда
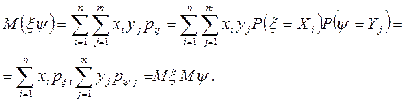
Аналогично доказывается и для дискретной случайной величины. n
Заметим, что свойство 3 допускает обобщение на сумму любого числа слагаемых, а свойство 4 допускает обобщение на произведение любого числа независимых (в совокупности) сомножителей.
Пример 9. Найти математическое ожидание случайной величины 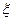 — число успехов в схеме Бернулли.
— число успехов в схеме Бернулли.
m Решение. Представим число успехов 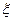 в схеме Бернулли из n испытаний в виде
в схеме Бернулли из n испытаний в виде 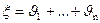 , где
, где  — число успехов в i-ом испытании. Очевидно, что
— число успехов в i-ом испытании. Очевидно, что  . По свойству 3 математического ожидания, получаем
. По свойству 3 математического ожидания, получаем
 .
.
Этот результат совпадает с результатом примера 3, но получен более легкими вычислениями. l
Пример 10. Производится ряд независимых опытов, в каждом из которых может появиться событие A. Вероятность события A в каждом опыте равна p. Опыты производятся до первого появления события А, после чего они прекращаются. Случайная величина 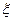 — число произведенных опытов. Найти
— число произведенных опытов. Найти  .
.
m Решение. Рассмотрим событие  , в этом случае событие A произошло при первом опыте, т.о.
, в этом случае событие A произошло при первом опыте, т.о. 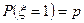 . Перейдем к событию
. Перейдем к событию  , в этом случае событие A при первом опыте не произошло, но произошло при втором опыте, т.о.
, в этом случае событие A при первом опыте не произошло, но произошло при втором опыте, т.о. 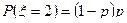 .
.
Производя аналогичные рассуждения, получаем ряд распределения:
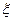
| 1 | 2 | 3 | … | 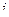
|
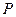
| 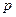
| 
| 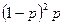
| … | 
|
Используя формулу (6.1.1), получим:
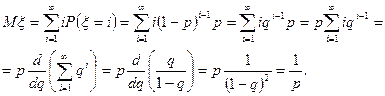
Таким образом, математическое ожидание равно  . l
. l
Пример 11. Независимые случайные величины 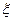 и
и 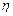 заданы своими рядами распределений:
заданы своими рядами распределений:


Для случайной величины 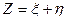 найти математическое ожидание двумя способами:
найти математическое ожидание двумя способами:
1) по определению математического ожидания;
2) по свойствам математического ожидания.
m Решение. Рассмотрим 1 способ нахождения математического ожидания. Для этого составим ряд распределения случайной величины 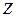 . Для этого удобно воспользоваться таблицей сумм
. Для этого удобно воспользоваться таблицей сумм 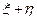 и соответствующих им вероятностей. Например:
и соответствующих им вероятностей. Например: 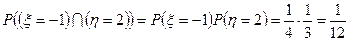 .
.
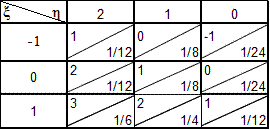
Далее очень легко получить ряд распределения случайной величины 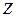 .
.
| Z | -1 | 0 | 1 | 2 | 3 |
| P | 1/24 | 1/6 | 7/24 | 1/3 | 1/6 |
Естественно, можно было бы обойтись и без таблицы. Например:
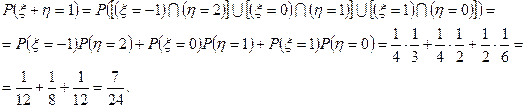
Используя ряд распределения, находим математическое ожидание
 .
.
Перейдем ко второму способу нахождения математического ожидания случайной величины 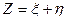 . Используя свойство 3, получим:
. Используя свойство 3, получим:
 .l
.l
Дата: 2019-02-25, просмотров: 307.