Пусть 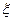 — случайная величина. Пусть задана функция
— случайная величина. Пусть задана функция 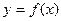 . Каждому элементарному исходу
. Каждому элементарному исходу  поставим в соответствие число
поставим в соответствие число 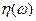 по формуле
по формуле  . Тем самым получим случайную величину
. Тем самым получим случайную величину 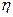 , называемую функцией
, называемую функцией 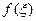 от случайной величины
от случайной величины 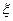 .
.
Пусть 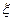 — дискретная случайная величина. Тогда случайная величина
— дискретная случайная величина. Тогда случайная величина  также является дискретной случайной величиной, поскольку она не может принимать больше значений, чем случайная величина
также является дискретной случайной величиной, поскольку она не может принимать больше значений, чем случайная величина  . Очевидно, что ряд распределения случайной величины
. Очевидно, что ряд распределения случайной величины 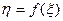 имеет вид:
имеет вид:
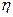
| 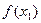
| 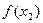
| … | 
|

| 
| 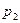
| … | 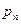
|
При этом, если в верхней строке ряда распределения появляются одинаковые значения  , то соответствующие столбцы необходимо объединить в один, приписав им суммарную вероятность.
, то соответствующие столбцы необходимо объединить в один, приписав им суммарную вероятность.
Пример 9. Случайная величина ξ имеет ряд распределения:
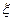
| -2 | -1 | 0 | 1 | 2 |

| 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Найти закон распределения случайной величины 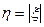 .
.
m Решение. Составим ряд распределения случайной величины  :
:
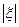
| 2 | 1 | 0 | 1 | 2 |

| 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Объединив первый и пятый, второй и четвертый столбцы, получим:
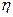
| 0 | 1 | 2 |

| 0,3 | 0,5 | 0,2 |
Ряд распределения случайной величины 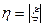 получен. l
получен. l
Пусть  — непрерывная случайная величина. При этом случайная величина
— непрерывная случайная величина. При этом случайная величина 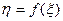 может быть как непрерывной, так и дискретной. Будем рассматривать непрерывные функции
может быть как непрерывной, так и дискретной. Будем рассматривать непрерывные функции 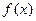 . Пусть случайная величина
. Пусть случайная величина 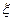 имеет плотность
имеет плотность 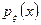 . Тогда
. Тогда
 . (5.5.1)
. (5.5.1)
Пример 10. Пусть случайная величина  имеет плотность
имеет плотность
 .
.
Найти распределение случайной величины  .
.
m Решение. В данном случае  . Согласно (5.5.1), получим
. Согласно (5.5.1), получим
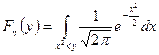 .
.
Очевидно, что при 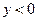 , функция распределения равна нулю, т.е.
, функция распределения равна нулю, т.е.  . При
. При 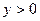 область
область 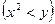 совпадает с областью
совпадает с областью  . Отсюда получаем
. Отсюда получаем
 . l
. l
Выведем более удобные формулы для вычисления функции 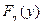 , где
, где 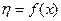 .
.
Теорема. Пусть 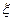 — непрерывная случайная величина с плотностью
— непрерывная случайная величина с плотностью 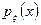 , а случайная величина
, а случайная величина  связана с
связана с 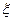 функциональной зависимостью
функциональной зависимостью
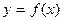 ,
,
где  — дифференцируемая функция, монотонная на всем участке возможных значений аргумента
— дифференцируемая функция, монотонная на всем участке возможных значений аргумента 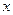 .
.
Тогда плотность распределения случайной величины  выражается формулой
выражается формулой
 , (5.5.2)
, (5.5.2)
где  — функция, обратная по отношению к функции
— функция, обратная по отношению к функции  .
.
Доказательство. Пусть  — монотонно возрастающая функция. Тогда
— монотонно возрастающая функция. Тогда
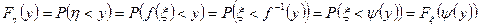 .
.
Продифференцировав последнее равенство, получаем
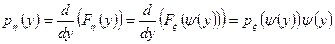 . (5.5.3)
. (5.5.3)
Пусть  — монотонно убывающая функция. В этом случае
— монотонно убывающая функция. В этом случае 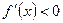 и, следовательно,
и, следовательно, 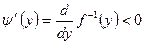 . Отсюда получаем:
. Отсюда получаем:

Продифференцировав последнее равенство, получаем
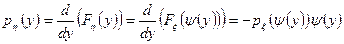 . (5.5.4)
. (5.5.4)
Учитывая свойства модуля, равенства (5.5.3) и (5.5.4) объединим в одно
 ,
,
что совпадает с (5.5.2). n
Пример 11. Случайная величина 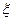 распределена равномерно в интервале
распределена равномерно в интервале 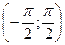 . Найти закон распределения случайной величины
. Найти закон распределения случайной величины 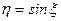 .
.
m Решение. Функция  в интервале
в интервале 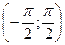 монотонна, следовательно, можно применить формулу (5.5.2). Решение задачи удобно расположить в виде таблицы, содержащей три столбца: в первом запишем план решения задачи; во втором столбце запишем обозначения функций, принятые в общем случае; в третьем — конкретные функции, соответствующие данному примеру:
монотонна, следовательно, можно применить формулу (5.5.2). Решение задачи удобно расположить в виде таблицы, содержащей три столбца: в первом запишем план решения задачи; во втором столбце запишем обозначения функций, принятые в общем случае; в третьем — конкретные функции, соответствующие данному примеру:
Плотность случайной величины 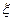
| 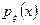
| 
|
Функциональная зависимость между случайными величинами 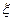 и и 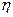
| 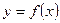
| 
|
| Обратная функция | 
| 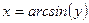
|
| Модуль производной обратной функции | 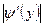
| 
|
Плотность случайной величины 
| 
| 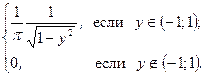
|
Интервал 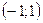 , в котором лежат значения случайной величины
, в котором лежат значения случайной величины  , определяется областью значений функции
, определяется областью значений функции 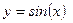 для
для 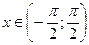 . l
. l
Следствие из теоремы. Если  — немонотонная функция, то обратная к ней функция неоднозначна, и плотность распределения случайной величины определяется в виде суммы стольких слагаемых, сколько значений (при данном значении
— немонотонная функция, то обратная к ней функция неоднозначна, и плотность распределения случайной величины определяется в виде суммы стольких слагаемых, сколько значений (при данном значении  ) имеет обратная функция:
) имеет обратная функция:
 , (5.5.5)
, (5.5.5)
где 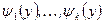 — значения обратной функции для данного
— значения обратной функции для данного  .
.
Пример 12. Случайная величина 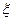 распределена равномерно в интервале
распределена равномерно в интервале 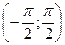 . Найти плотность распределения случайной величины
. Найти плотность распределения случайной величины  .
.
m Решение. Функция 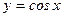 немонотонная в интервале
немонотонная в интервале 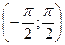 , ее значения лежат в интервале (0,1). В данном случае для любого
, ее значения лежат в интервале (0,1). В данном случае для любого  обратная функция будет иметь два значения:
обратная функция будет иметь два значения:
Плотность случайной величины 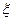
| 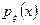
| 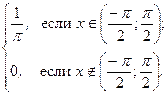
|
Функциональная зависимость между случайными величинами 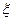 и и 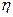 . .
| 
| 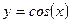
|
| Обратная функция | 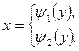
| 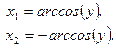
|
| Модуль производной обратной функции | 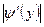
| 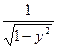
|
Плотность случайной величины 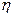
| 
| 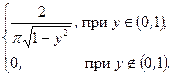
|
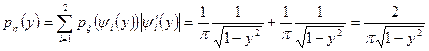 . l
. l
Дата: 2019-02-25, просмотров: 322.