По статистическом ряду, приведенному в таблице 7.3,

Таблица 7.3

№	1	2	…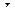
Варианты			…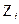
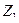
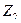
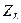
Относительная частота			…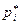

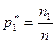
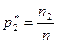
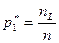
можно построить эмпирическую (выборочную) функцию распределения.

Определение. Эмпирической (выборочной) функцией распределения называется функция 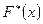, задающая для каждого значения  относительную частоту события .

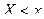Следовательно, по определению

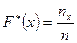, (7.3.1)

где 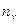 — число элементов выборки, значения которых меньше .

Очевидно, что для нахождения функции распределения можно использовать формулу

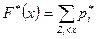. (7.3.2)

Эмпирическую функцию распределения можно задать таблично или графически. Построим эмпирическую функцию распределения по данным, приведенным в таблице 7.2.

Объем выборки по условию примера 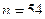. Наименьшая варианта равна 0, следовательно,  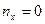при 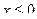. Тогда  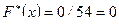при 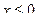. Если 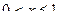, то неравенство  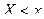выполняется для варианты 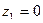, которая встречается 31 раз, поэтому  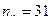и 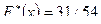. Если 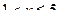, то неравенство  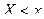выполняется для вариант  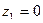и 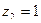, которые встречаются 31 и 14 раз соответственно, поэтому, 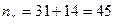,  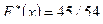и т.д. Результаты вычисления  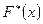приведем в таблице 7.4

Таблица 7.4

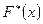
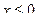
	0

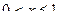
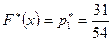
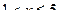
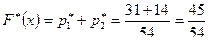
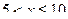
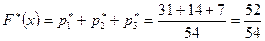
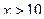
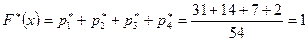
График этой функции приведен на рис. 7.1.

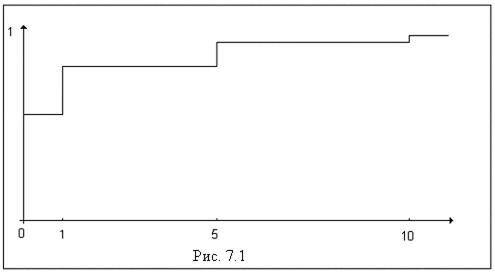
В случае интервального ряда значения эмпирической функции 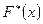 подсчитывают на концах частичных интервалов.

Эмпирическая функция 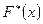 применяется для оценивания теоретической функции распределения генеральной совокупности.

Полигон и гистограмма

Определение. Полигоном частот (многоугольником распределения) называется ломаная линия, проходящая через точки с координатами 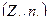, где 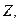— варианты статистического ряда, а 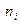— соответствующие им частоты.

Если ломаная линия строится по точкам 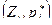, где — относительные частоты, то получаем полигон относительных частот.

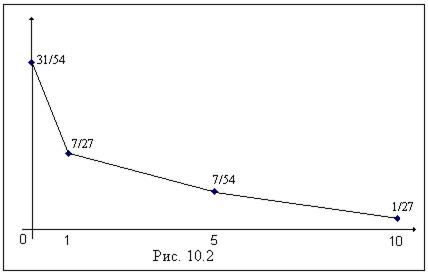
Построим полигон относительных частот для выборки из примера 2. Используя статистический ряд, представленный в таблице 7.2, получаем полигон относительных частот, изображенный на рис. 7.2.

В случае непрерывной случайной величины выборку преобразуют следующим образом. Всю ось абсцисс делят на интервал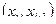ы  длины 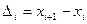 и определяют функцию 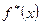, которая на 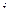‑м интервале принимает значение

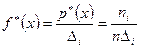, (7.4.1)

где 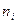 — число элементов выборки, попавших в интервал.

Определение. Функция 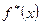, определенная соотношением (7.4.1), называется гистограммой.

Гистограмма является выборочной оценкой плотности вероятности.

Построим гистограмму по данным, приведенным в примере 1. Длина каждого интервала равна 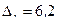. Подсчитаем значения :

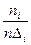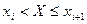
	2,9 — 9,1	9,1 — 15,3	15,3—21,5	21,5—27,7	27,7—33,9	33,9—40,1
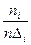
	0,038710	0,038710	0,045161	0,019355	0,012903	0,006452

На рис. 7.3 представлена гистограмма примера 1.

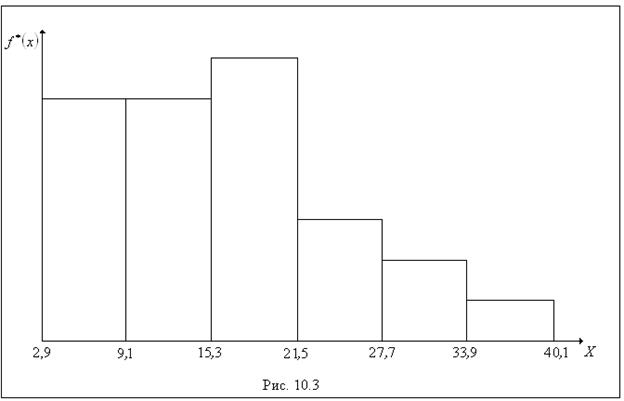
Графическое изображение статистических рядов в виде полигона и гистограммы позволяет получить первоначальное представление о закономерностях, имеющих место в совокупности наблюдений.