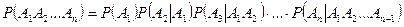 . (3.2.4)
. (3.2.4)
Пример 2. Бросают две монеты. Рассматриваются два события:
A — выпадение «герба» на первой монете;
B — выпадение «герба» на второй монете.
Найти вероятность события 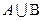 .
.
m Решение. Очевидно, что пространство элементарных исходов состоит из четырех исходов: «герб»‑«герб», «герб»‑«решка», «решка»‑«герб», «решка»‑«решка».
Применим теорему сложения вероятностей 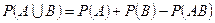 .
.
Очевидно, что 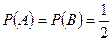 и
и 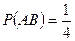 , так как событию
, так как событию 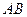 благоприятствует всего один исход, а число возможных исходов равно 4. Окончательно получим:
благоприятствует всего один исход, а число возможных исходов равно 4. Окончательно получим:
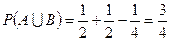 .
.
Заметим, что задачу можно решить с помощью противоположного события. Рассмотрим событие 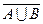 — выпадение пары «решка»‑«решка», тогда
— выпадение пары «решка»‑«решка», тогда
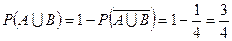 . l
. l
Пример 3. В урне 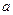 белых и
белых и 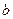 черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.
черных шаров. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.
m Решение. Рассмотрим события:
 — первый шар белый;
— первый шар белый;
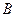 — второй шар белый.
— второй шар белый.
Применяя теорему умножения вероятностей, получаем:
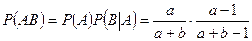 .
.
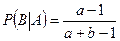 , так как общее число шаров, а также число белых, уменьшилось на 1. l
, так как общее число шаров, а также число белых, уменьшилось на 1. l
Пример 4. На семи карточках написаны буквы, образующие слово «телефон». После перестановки карточек наудачу последовательно берут пять из них, и прикладывают справа одну к другой. Найти вероятность образования слова «фенол».
m Решение. Применим теорему умножения вероятностей для нескольких событий. Вероятность 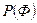 того, что первой буквой будет «Ф», равна
того, что первой буквой будет «Ф», равна 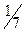 . Вероятность
. Вероятность 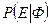 того, что второй буквой будет «Е», при условии, что букву «Ф» уже взяли, равна
того, что второй буквой будет «Е», при условии, что букву «Ф» уже взяли, равна 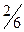 и т.д. В итоге получаем:
и т.д. В итоге получаем:
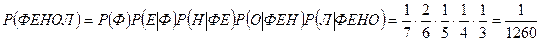 .l
.l
Пример 5. В урне 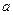 белых и
белых и 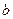 черных шаров. Из урны вынимаются два шара. Найти вероятность того, что эти шары будут разных цветов.
черных шаров. Из урны вынимаются два шара. Найти вероятность того, что эти шары будут разных цветов.
m Решение. Рассмотрим события:
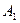 — первый шар белый;
— первый шар белый;
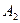 — второй шар белый;
— второй шар белый;
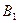 — первый шар черный;
— первый шар черный;
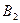 — второй шар черный;
— второй шар черный;
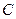 — шары разных цветов.
— шары разных цветов.
Очевидно, что 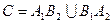 , причем события
, причем события 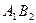 и
и 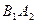 несовместимы. По теореме сложения и по теореме умножения вероятностей для независимых событий:
несовместимы. По теореме сложения и по теореме умножения вероятностей для независимых событий:
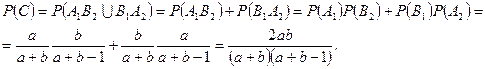
l
Пример 6. Техническая система состоит из n элементов, надежность каждого из них 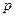 . Выход из строя хотя бы одного влечет за собой выход всей системы. С целью повышения надежности системы производится дублирование, для чего выделено еще n таких же приборов. Определить, какой из способов дублирования надежнее:
. Выход из строя хотя бы одного влечет за собой выход всей системы. С целью повышения надежности системы производится дублирование, для чего выделено еще n таких же приборов. Определить, какой из способов дублирования надежнее:
§ дублирование каждого элемента (рис. 3.1);
§ дублирование всей системы (рис. 3.2).
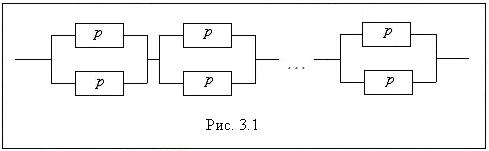
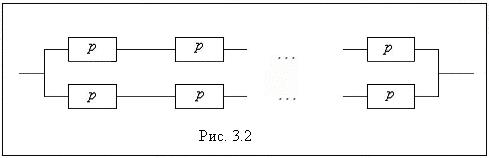
m Решение. Найдем надежность блока:
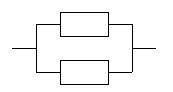
Для этого найдем вероятность выхода из строя. Блок выходит из строя, если выходит из строя каждый элемент, т.е. 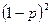 . Тогда надежность блока равна
. Тогда надежность блока равна 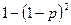 . Далее система работает надежно, если работает каждый блок, т.о.:
. Далее система работает надежно, если работает каждый блок, т.о.:
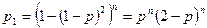 .
.
Надежность системы

равна 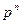 . Отсюда надежность системы (рис. 3.2)
. Отсюда надежность системы (рис. 3.2)
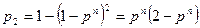 .
.
Сравним 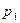 и
и 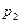 , для этого нужно сравнить
, для этого нужно сравнить 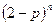 и
и 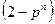 .
.
Докажем, что 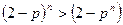 .
.
Подставим 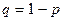 , т.е.
, т.е. 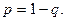
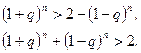
Далее достаточно раскрыть скобки.
Таким образом, надежнее дублирование каждого элемента. l
Независимость событий
Определение. События A и B называются независимыми, если условная вероятность события A при условии B совпадает с безусловной вероятностью события A, т.е.
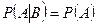 . (3.3.1)
. (3.3.1)
Можно сформулировать и другое определение независимых событий  и
и 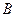 .
.
Определение. События A и B независимы, если
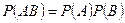 . (3.3.2)
. (3.3.2)
Очевидно, что данные два определения равносильны.
Пример 7. Пусть события  и
и 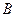 независимы. Доказать, что независимыми являются пары событий
независимы. Доказать, что независимыми являются пары событий 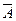 и
и 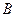 ,
,  и
и 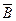 ,
, 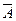 и
и 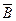 .
.
m Решение. Применяя определение независимости событий, и используя вероятность противоположного события, имеем
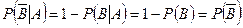 , т.е.
, т.е. 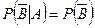 ;
;
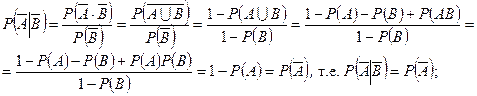
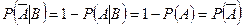 , т.е.
, т.е. 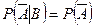 . l
. l
Пример 8. Зависимы или независимы несовместные события.
m Решение. Пусть события  и
и 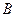 несовместные, т.е.
несовместные, т.е. 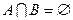 , причем
, причем 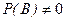 . Тогда
. Тогда 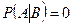 , т.к. события не пересекаются. Следовательно
, т.к. события не пересекаются. Следовательно  и
и 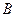 зависимы.
зависимы.
Таким образом, несовместные события зависимы. l
Пример 9. Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются следующие события:
 — появление туза;
— появление туза;
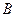 — появление карты красной масти;
— появление карты красной масти;
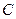 — появление бубнового туза.
— появление бубнового туза.
Зависимы или независимы следующие пары событий: 1)  и
и 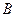 , 2)
, 2) 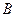 и
и 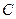 , 3)
, 3)  и
и 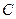 ?
?
M Решение.
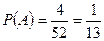 ,
, 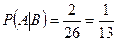 , следовательно, события независимы;
, следовательно, события независимы;
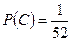 ,
, 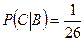 , следовательно, события зависимы;
, следовательно, события зависимы;
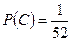 ,
, 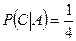 , следовательно, события зависимы. l
, следовательно, события зависимы. l
Определение. События 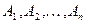 независимы в совокупности, если для всех
независимы в совокупности, если для всех
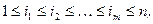
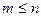 , выполнено равенство
, выполнено равенство
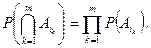
Замечание. Из попарной независимости событий 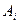 и
и 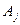
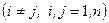 не следует, что события
не следует, что события 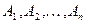 независимы в совокупности.
независимы в совокупности.
Пример 10. Пусть эксперимент состоит в выборе одного из четырех шаров. Пусть три из них занумерованы цифрами 1, 2, 3, а на четвертом шаре имеются все эти цифры. Обозначим через 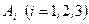 событие, состоящее в том, что на выбранном шаре имеется цифра
событие, состоящее в том, что на выбранном шаре имеется цифра 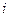 . Зависимы ли события
. Зависимы ли события 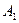 ,
, 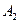 и
и 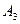 .
.
m Решение. Так как, каждая цифра встречается дважды, то
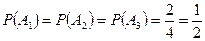 .
.
Так как две различные цифры присутствуют только на одном шаре, то
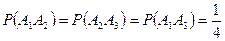 ,
,
следовательно, события 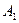 ,
, 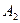 и
и 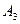 попарно независимы.
попарно независимы.
Все три различные цифры присутствуют только на одном шаре
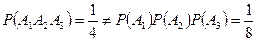 .
.
Таким образом, получаем, что события 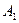 ,
, 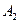 и
и 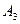 зависимы в совокупности, в то время как они являются попарно независимыми. l
зависимы в совокупности, в то время как они являются попарно независимыми. l
Формула полной вероятности
Определение. События 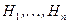 образуют полную группу несовместных событий (являются гипотезами), если они удовлетворяют двум требованиям:
образуют полную группу несовместных событий (являются гипотезами), если они удовлетворяют двум требованиям:
§ они попарно несовместны, т.е. 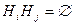 при
при 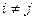 ;
;
§ в результате опыта одно из событий обязательно должно произойти, т.е.  .
.
Пусть имеется некоторое событие  и известны вероятности
и известны вероятности 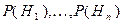 и условные вероятности
и условные вероятности 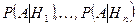 . Найдем вероятность
. Найдем вероятность 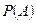 .
.
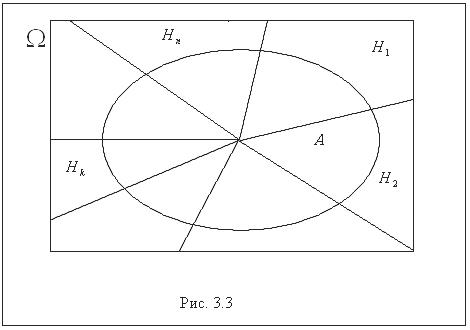
Событие  можно представить в виде (рис. 3.3):
можно представить в виде (рис. 3.3):
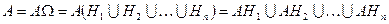 ,
,
причем события 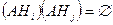 при
при 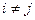 , т.е. события
, т.е. события  и
и 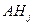 несовместны.
несовместны.
Тогда по аксиоме сложения:
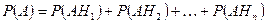 .
.
Далее, применяя теорему умножения вероятностей 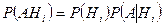 , получаем:
, получаем:
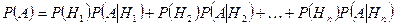 . (3.4.1)
. (3.4.1)
Это и есть формула полной вероятности.
Пример 11. Имеются две урны: в первой 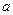 белых и
белых и 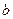 черных шаров; во второй
черных шаров; во второй 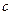 белых и
белых и 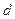 черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
m Решение. Пусть искомое событие  — вынут белый шар. Рассмотрим следующие гипотезы:
— вынут белый шар. Рассмотрим следующие гипотезы:
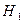 — переложен белый шар;
— переложен белый шар;
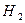 — переложен черный шар.
— переложен черный шар.
Очевидно, что
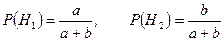 ;
;
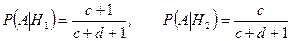 .
.
Теперь по формуле полной вероятности (3.4.1) получаем:
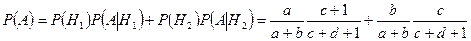 . l
. l
Пример 12. В условиях предыдущей задачи из первой урны перекладывают сразу три шара (предполагается, что 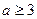 и
и 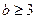 ). Найти вероятность того, что шар, взятый из второй урны, будет белым.
). Найти вероятность того, что шар, взятый из второй урны, будет белым.
m Решение. Пусть искомое событие  — вынут белый шар. Рассмотрим гипотезы:
— вынут белый шар. Рассмотрим гипотезы:
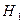 — вынутый шар принадлежит 1-ой урне;
— вынутый шар принадлежит 1-ой урне;
 — вынутый шар принадлежит 2-ой урне.
— вынутый шар принадлежит 2-ой урне.
Так как во второй урне 3 шара принадлежат 1-ой урне, а 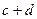 принадлежат 2-ой, то вероятности гипотез равны:
принадлежат 2-ой, то вероятности гипотез равны:
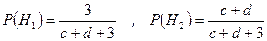 .
.
Вероятность появления белого шара из первой урны не зависит от того, вынимается ли этот шар непосредственно из первой урны или после перекладывания во вторую. Следовательно, условная вероятность появления белого шара при условии того, что он изначально находился в первой урне, равна:
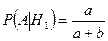 .
.
Аналогично условная вероятность появления белого шара при условии того, что он изначально находился во второй урне, равна:
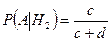 .
.
По формуле полной вероятности (3.4.1) получаем:
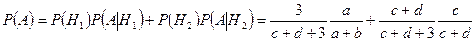 . l
. l
Пример 13. Среди 30 экзаменационных билетов: 25 «хороших» и 5 «плохих». Какова вероятность, отвечая вторым, взять «хороший» билет?
m Решение. Пусть искомое событие  — второй отвечающий взял «хороший» билет. Рассмотрим следующие гипотезы:
— второй отвечающий взял «хороший» билет. Рассмотрим следующие гипотезы:
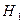 — первый отвечающий взял «хороший» билет;
— первый отвечающий взял «хороший» билет;
 — первый отвечающий взял «плохой» билет.
— первый отвечающий взял «плохой» билет.
Очевидно, что
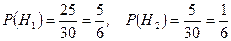 ;
;
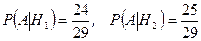 .
.
По формуле полной вероятности (3.4.1), получим:
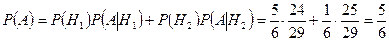 . l
. l
Формула Байеса
Пусть имеется полная группа несовместных событий 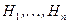 . Требуется найти вероятность события
. Требуется найти вероятность события 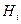 , если известно, что событие
, если известно, что событие 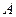 произошло.
произошло.
По определению условной вероятности (3.4.1), имеем:
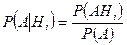 .
.
Далее, применяя теорему умножения вероятностей 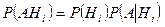 , получаем
, получаем
 . (3.5.1)
. (3.5.1)
Последняя формула называется формулой Байеса или формулой гипотез (события 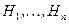 называют еще гипотезами).
называют еще гипотезами).
Если после опыта, который заканчивается появлением события 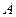 , производится еще один опыт, в котором появляется или не появляется событие
, производится еще один опыт, в котором появляется или не появляется событие  , то условная вероятность этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез
, то условная вероятность этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез 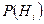 , а новые
, а новые 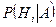 :
:
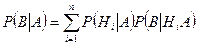 . (3.5.2)
. (3.5.2)
Пример 14. Имеются три урны: в первой — 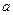 белых и
белых и 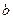 черных шаров; во второй —
черных шаров; во второй — 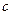 белых и
белых и 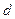 черных шаров, в третьей —
черных шаров, в третьей — 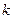 белых шаров. Выбирается наугад урна и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.
белых шаров. Выбирается наугад урна и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.
m Решение. Пусть искомое событие 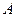 — вынутый шар белый. Рассмотрим следующие гипотезы:
— вынутый шар белый. Рассмотрим следующие гипотезы:
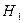 — выбрана первая урна;
— выбрана первая урна;
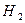 — выбрана вторая урна;
— выбрана вторая урна;
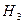 — выбрана третья урна.
— выбрана третья урна.
Очевидно, что:
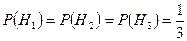 .
.
Условные вероятности равны:
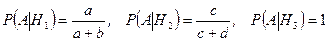 .
.
По формуле полной вероятности (3.4.1), находим, что
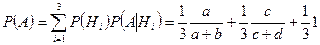 .
.
По формуле Байеса (3.5.1), находим:
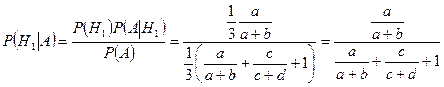 .
.
Аналогично получаем, что
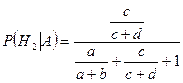 ,
, 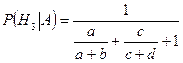 . l
. l
Пример 15. Имеются две урны: в первой — 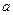 белых и
белых и 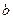 черных шаров; во второй —
черных шаров; во второй — 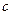 белых и
белых и 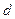 черных шаров. Выбирается наугад одна из урн и из нее вынимается один шар. Этот шар оказался белым (событие А). найти вероятность того, что следующий шар, который мы вынимаем из той же урны, будет тоже белым(событие В).
черных шаров. Выбирается наугад одна из урн и из нее вынимается один шар. Этот шар оказался белым (событие А). найти вероятность того, что следующий шар, который мы вынимаем из той же урны, будет тоже белым(событие В).
m Решение. Рассмотрим следующие гипотезы:
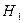 — выбрана первая урна;
— выбрана первая урна;
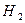 — выбрана вторая урна.
— выбрана вторая урна.
Очевидно, что вероятности выбора урн равны:
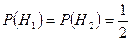 .
.
Находим условные вероятности:
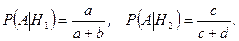
По формуле полной вероятности (3.4.1), получаем:
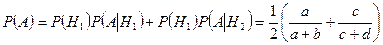 .
.
По формуле Байеса (3.5.1), получаем:

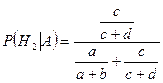 .
.
Далее применяем (3.5.2):
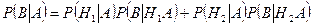 .
.
Условная вероятность появления второго белого шара при условии, что была выбрана первая урна, и из нее вынут белый шар:
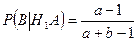 .
.
Аналогично:
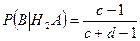 .
.
В итоге:
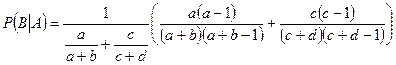 . l
. l
Дата: 2019-02-25, просмотров: 301.