ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
 |
Московский государственный университет
Приборостроения и информатики

Кафедра высшей математики
Манжиров А.В., Михин М.Н.
Теория вероятностей и математическая
статистика (решение задач)
Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.
Москва 2005
Редактор: Выборнов А.Н.
Глава 1. Случайные события и их вероятности
Замечание.
Элементарными исходами суммы событий 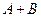 являются элементарные исходы, принадлежащие хотя бы одному из событий
являются элементарные исходы, принадлежащие хотя бы одному из событий  и
и 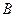 .
.
Элементарными исходами произведения событий 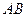 являются те элементарные исходы, которые одновременно принадлежат событиям
являются те элементарные исходы, которые одновременно принадлежат событиям  и
и 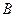 .
.
Элементарными исходами разности событий 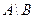 являются те элементарные исходы события
являются те элементарные исходы события  , которые не принадлежат событию
, которые не принадлежат событию 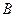 .
.
Элементарными исходами противоположного события  являются те элементарные исходы, которые не принадлежат событию
являются те элементарные исходы, которые не принадлежат событию  .
.
Общее определение и свойства вероятности
Определение. Вероятностью 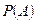 события
события  называется функция, определенная на пространстве элементарных исходов и удовлетворяющая трем условиям:
называется функция, определенная на пространстве элементарных исходов и удовлетворяющая трем условиям:
§ Для каждого события 
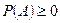 (условие неотрицательности);
(условие неотрицательности);
§ Для достоверного события 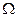
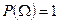 (условие нормировки);
(условие нормировки);
§ Если 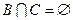 , то
, то
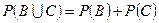 (теорема сложения для несовместных событий).
(теорема сложения для несовместных событий).
Свойства вероятности:
1. Вероятность события  , противоположного событию
, противоположного событию  , равна
, равна
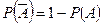 .
.
Доказательство. Используем очевидное свойство суммы противоположных событий 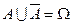 . Тогда, используя условие нормировки и теорему сложения для несовместных событий, получим:
. Тогда, используя условие нормировки и теорему сложения для несовместных событий, получим:
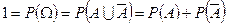 ,
,
Из двух последнего равенства следует, что
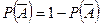 . n
. n
2. Вероятность невозможного события равна нулю, т.е.
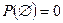 .
.
Доказательство. Используем очевидное свойство 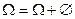 и теорему сложения для несовместных событий, получим:
и теорему сложения для несовместных событий, получим:
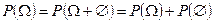 ,
,
откуда и следует данное свойство. n
3. Если событие  влечёт за собой событие
влечёт за собой событие 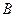
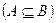 , то
, то
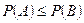 .
.
Доказательство. Представим событие 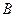 в виде суммы двух несовместных событий
в виде суммы двух несовместных событий 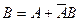 ,
, 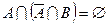 .
.
Используя теорему сложения для несовместных событий, получим:
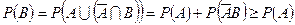 . n
. n
4. Для каждого события  , справедливо неравенство
, справедливо неравенство
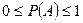 .
.
Доказательство. Данное свойство следует из условий нормировки и теоремы сложения для несовместных событий. n
ГЛАВА 2. Классическая и геометрическая вероятности
Условная вероятность
Рассмотрим следующий пример. Бросаются две игральные кости. Найдем вероятность того, что сумма выпавших очков равна 8, если заранее известно, что сумма выпавших очков есть четное число. Всевозможные исходы запишем в виде таблицы 3.1:
Таблица 3.1
| 2ой кубик 1ый кубик | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Из таблицы видно, что число всевозможных исходов равно 36, но число исходов, удовлетворяющих условию, при которых сумма очков есть четное число, равно 18. Из них ровно в 5 исходах сумма очков равна 8. Пользуясь классическим определением вероятности, находим, что искомая вероятность равна 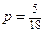 .
.
Заметим, что безусловная вероятность того, что сумма выпавших очков, равная 8, равна 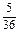 , т.е. задание дополнительного условия может повлиять на вычисление вероятности.
, т.е. задание дополнительного условия может повлиять на вычисление вероятности.
Найдем условную вероятность 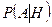 события
события  при условии, что событие
при условии, что событие 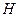 уже произошло. Для простоты рассмотрим классическую схему. Естественно положить, что данная вероятность есть отношение числа исходов
уже произошло. Для простоты рассмотрим классическую схему. Естественно положить, что данная вероятность есть отношение числа исходов 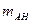 , благоприятных совместному (одновременному) осуществлению событий
, благоприятных совместному (одновременному) осуществлению событий  и
и 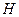 , к числу исходов, благоприятных событию
, к числу исходов, благоприятных событию 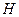 , т.е.
, т.е.
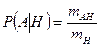 .
.
Разделив числитель и знаменатель на число всевозможных исходов 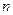 , получим:
, получим:
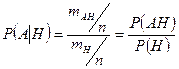 .
.
Последняя формула может служить общим определением условной вероятности при аксиоматическом подходе.
Определение. Условной вероятностью 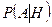 события
события  при условии, что событие
при условии, что событие 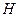 уже произошло, называется отношение вероятности совместного (одновременного) осуществления событий
уже произошло, называется отношение вероятности совместного (одновременного) осуществления событий  и
и 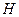 к вероятности события
к вероятности события 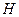 :
:
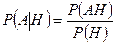 . (3.1.1)
. (3.1.1)
Пример 1. При трехкратном подбрасывании монеты выпало два «герба». Найти условную вероятность того, что при втором подбрасывании выпал «герб».
m Решение. Рассмотрим следующие события:
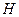 — при трехкратном подбрасывании выпало два «герба»;
— при трехкратном подбрасывании выпало два «герба»;
 — при втором подбрасывании выпал «герб».
— при втором подбрасывании выпал «герб».
Событию 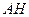 соответствует два исхода: Г – Г – Р, Р – Г – Г.
соответствует два исхода: Г – Г – Р, Р – Г – Г.
Число всевозможных исходов при трехкратном подбрасывании монеты 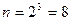 . Отсюда находим:
. Отсюда находим:
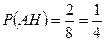 .
.
Аналогично, событию 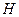 соответствует три исхода, следовательно, вероятность условия равна
соответствует три исхода, следовательно, вероятность условия равна
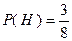 .
.
Далее, применяя (3.1.1), получаем искомую вероятность
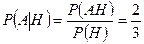 . l
. l
Независимость событий
Определение. События A и B называются независимыми, если условная вероятность события A при условии B совпадает с безусловной вероятностью события A, т.е.
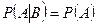 . (3.3.1)
. (3.3.1)
Можно сформулировать и другое определение независимых событий  и
и 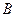 .
.
Определение. События A и B независимы, если
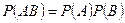 . (3.3.2)
. (3.3.2)
Очевидно, что данные два определения равносильны.
Пример 7. Пусть события  и
и 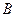 независимы. Доказать, что независимыми являются пары событий
независимы. Доказать, что независимыми являются пары событий 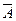 и
и 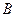 ,
,  и
и 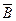 ,
, 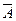 и
и 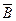 .
.
m Решение. Применяя определение независимости событий, и используя вероятность противоположного события, имеем
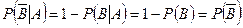 , т.е.
, т.е. 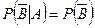 ;
;
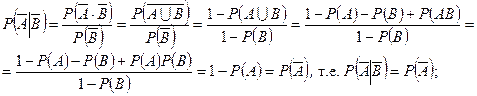
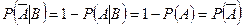 , т.е.
, т.е. 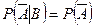 . l
. l
Пример 8. Зависимы или независимы несовместные события.
m Решение. Пусть события  и
и 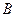 несовместные, т.е.
несовместные, т.е. 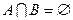 , причем
, причем 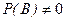 . Тогда
. Тогда 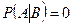 , т.к. события не пересекаются. Следовательно
, т.к. события не пересекаются. Следовательно  и
и 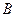 зависимы.
зависимы.
Таким образом, несовместные события зависимы. l
Пример 9. Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются следующие события:
 — появление туза;
— появление туза;
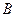 — появление карты красной масти;
— появление карты красной масти;
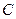 — появление бубнового туза.
— появление бубнового туза.
Зависимы или независимы следующие пары событий: 1)  и
и 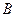 , 2)
, 2) 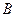 и
и 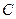 , 3)
, 3)  и
и 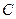 ?
?
M Решение.
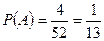 ,
, 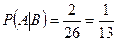 , следовательно, события независимы;
, следовательно, события независимы;
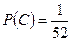 ,
, 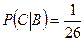 , следовательно, события зависимы;
, следовательно, события зависимы;
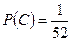 ,
, 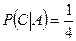 , следовательно, события зависимы. l
, следовательно, события зависимы. l
Определение. События 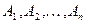 независимы в совокупности, если для всех
независимы в совокупности, если для всех
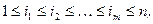
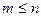 , выполнено равенство
, выполнено равенство
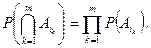
Замечание. Из попарной независимости событий 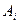 и
и 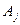
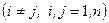 не следует, что события
не следует, что события 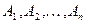 независимы в совокупности.
независимы в совокупности.
Пример 10. Пусть эксперимент состоит в выборе одного из четырех шаров. Пусть три из них занумерованы цифрами 1, 2, 3, а на четвертом шаре имеются все эти цифры. Обозначим через 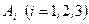 событие, состоящее в том, что на выбранном шаре имеется цифра
событие, состоящее в том, что на выбранном шаре имеется цифра 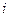 . Зависимы ли события
. Зависимы ли события 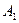 ,
, 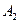 и
и 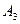 .
.
m Решение. Так как, каждая цифра встречается дважды, то
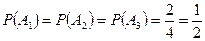 .
.
Так как две различные цифры присутствуют только на одном шаре, то
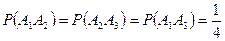 ,
,
следовательно, события 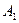 ,
, 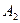 и
и 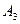 попарно независимы.
попарно независимы.
Все три различные цифры присутствуют только на одном шаре
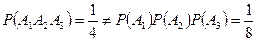 .
.
Таким образом, получаем, что события 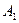 ,
, 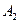 и
и 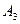 зависимы в совокупности, в то время как они являются попарно независимыми. l
зависимы в совокупности, в то время как они являются попарно независимыми. l
Формула полной вероятности
Определение. События 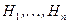 образуют полную группу несовместных событий (являются гипотезами), если они удовлетворяют двум требованиям:
образуют полную группу несовместных событий (являются гипотезами), если они удовлетворяют двум требованиям:
§ они попарно несовместны, т.е. 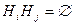 при
при 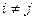 ;
;
§ в результате опыта одно из событий обязательно должно произойти, т.е.  .
.
Пусть имеется некоторое событие  и известны вероятности
и известны вероятности 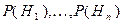 и условные вероятности
и условные вероятности 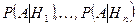 . Найдем вероятность
. Найдем вероятность 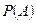 .
.
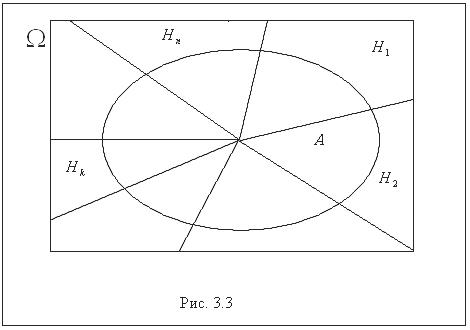
Событие  можно представить в виде (рис. 3.3):
можно представить в виде (рис. 3.3):
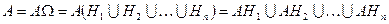 ,
,
причем события 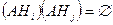 при
при 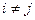 , т.е. события
, т.е. события  и
и 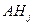 несовместны.
несовместны.
Тогда по аксиоме сложения:
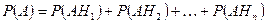 .
.
Далее, применяя теорему умножения вероятностей 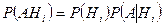 , получаем:
, получаем:
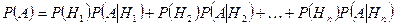 . (3.4.1)
. (3.4.1)
Это и есть формула полной вероятности.
Пример 11. Имеются две урны: в первой 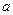 белых и
белых и 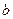 черных шаров; во второй
черных шаров; во второй 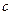 белых и
белых и 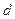 черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
m Решение. Пусть искомое событие  — вынут белый шар. Рассмотрим следующие гипотезы:
— вынут белый шар. Рассмотрим следующие гипотезы:
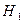 — переложен белый шар;
— переложен белый шар;
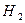 — переложен черный шар.
— переложен черный шар.
Очевидно, что
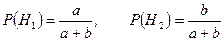 ;
;
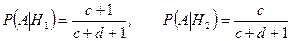 .
.
Теперь по формуле полной вероятности (3.4.1) получаем:
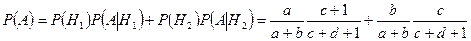 . l
. l
Пример 12. В условиях предыдущей задачи из первой урны перекладывают сразу три шара (предполагается, что 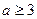 и
и 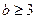 ). Найти вероятность того, что шар, взятый из второй урны, будет белым.
). Найти вероятность того, что шар, взятый из второй урны, будет белым.
m Решение. Пусть искомое событие  — вынут белый шар. Рассмотрим гипотезы:
— вынут белый шар. Рассмотрим гипотезы:
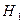 — вынутый шар принадлежит 1-ой урне;
— вынутый шар принадлежит 1-ой урне;
 — вынутый шар принадлежит 2-ой урне.
— вынутый шар принадлежит 2-ой урне.
Так как во второй урне 3 шара принадлежат 1-ой урне, а 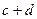 принадлежат 2-ой, то вероятности гипотез равны:
принадлежат 2-ой, то вероятности гипотез равны:
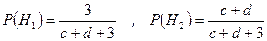 .
.
Вероятность появления белого шара из первой урны не зависит от того, вынимается ли этот шар непосредственно из первой урны или после перекладывания во вторую. Следовательно, условная вероятность появления белого шара при условии того, что он изначально находился в первой урне, равна:
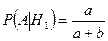 .
.
Аналогично условная вероятность появления белого шара при условии того, что он изначально находился во второй урне, равна:
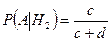 .
.
По формуле полной вероятности (3.4.1) получаем:
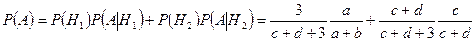 . l
. l
Пример 13. Среди 30 экзаменационных билетов: 25 «хороших» и 5 «плохих». Какова вероятность, отвечая вторым, взять «хороший» билет?
m Решение. Пусть искомое событие  — второй отвечающий взял «хороший» билет. Рассмотрим следующие гипотезы:
— второй отвечающий взял «хороший» билет. Рассмотрим следующие гипотезы:
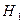 — первый отвечающий взял «хороший» билет;
— первый отвечающий взял «хороший» билет;
 — первый отвечающий взял «плохой» билет.
— первый отвечающий взял «плохой» билет.
Очевидно, что
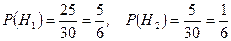 ;
;
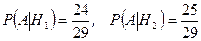 .
.
По формуле полной вероятности (3.4.1), получим:
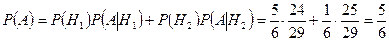 . l
. l
Формула Байеса
Пусть имеется полная группа несовместных событий 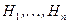 . Требуется найти вероятность события
. Требуется найти вероятность события 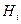 , если известно, что событие
, если известно, что событие 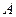 произошло.
произошло.
По определению условной вероятности (3.4.1), имеем:
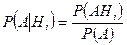 .
.
Далее, применяя теорему умножения вероятностей 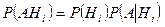 , получаем
, получаем
 . (3.5.1)
. (3.5.1)
Последняя формула называется формулой Байеса или формулой гипотез (события 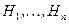 называют еще гипотезами).
называют еще гипотезами).
Если после опыта, который заканчивается появлением события 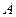 , производится еще один опыт, в котором появляется или не появляется событие
, производится еще один опыт, в котором появляется или не появляется событие  , то условная вероятность этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез
, то условная вероятность этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез 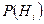 , а новые
, а новые 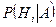 :
:
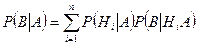 . (3.5.2)
. (3.5.2)
Пример 14. Имеются три урны: в первой — 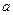 белых и
белых и 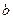 черных шаров; во второй —
черных шаров; во второй — 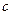 белых и
белых и 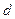 черных шаров, в третьей —
черных шаров, в третьей — 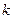 белых шаров. Выбирается наугад урна и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.
белых шаров. Выбирается наугад урна и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.
m Решение. Пусть искомое событие 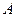 — вынутый шар белый. Рассмотрим следующие гипотезы:
— вынутый шар белый. Рассмотрим следующие гипотезы:
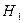 — выбрана первая урна;
— выбрана первая урна;
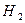 — выбрана вторая урна;
— выбрана вторая урна;
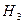 — выбрана третья урна.
— выбрана третья урна.
Очевидно, что:
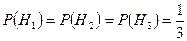 .
.
Условные вероятности равны:
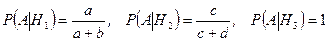 .
.
По формуле полной вероятности (3.4.1), находим, что
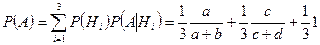 .
.
По формуле Байеса (3.5.1), находим:
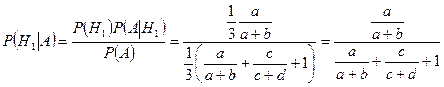 .
.
Аналогично получаем, что
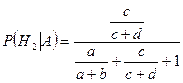 ,
, 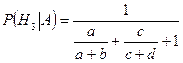 . l
. l
Пример 15. Имеются две урны: в первой — 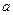 белых и
белых и 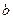 черных шаров; во второй —
черных шаров; во второй — 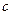 белых и
белых и 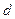 черных шаров. Выбирается наугад одна из урн и из нее вынимается один шар. Этот шар оказался белым (событие А). найти вероятность того, что следующий шар, который мы вынимаем из той же урны, будет тоже белым(событие В).
черных шаров. Выбирается наугад одна из урн и из нее вынимается один шар. Этот шар оказался белым (событие А). найти вероятность того, что следующий шар, который мы вынимаем из той же урны, будет тоже белым(событие В).
m Решение. Рассмотрим следующие гипотезы:
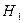 — выбрана первая урна;
— выбрана первая урна;
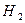 — выбрана вторая урна.
— выбрана вторая урна.
Очевидно, что вероятности выбора урн равны:
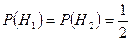 .
.
Находим условные вероятности:
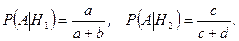
По формуле полной вероятности (3.4.1), получаем:
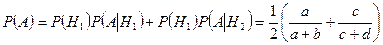 .
.
По формуле Байеса (3.5.1), получаем:

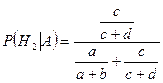 .
.
Далее применяем (3.5.2):
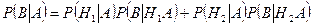 .
.
Условная вероятность появления второго белого шара при условии, что была выбрана первая урна, и из нее вынут белый шар:
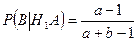 .
.
Аналогично:
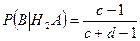 .
.
В итоге:
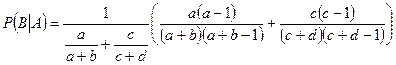 . l
. l
Формула Бернулли
Определение. Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два исхода, и вероятности исходов остаются неизменными для всех испытаний.
Обычно эти две вероятности обозначаются через  и
и  , исход с вероятностью
, исход с вероятностью 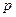 называют «успехом» и обозначают символом 1, а второй – «неудачей» и обозначают символом 0. Очевидно, что
называют «успехом» и обозначают символом 1, а второй – «неудачей» и обозначают символом 0. Очевидно, что  и
и  должны быть неотрицательными и должно выполняться равенство
должны быть неотрицательными и должно выполняться равенство
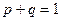 . (4.1.1)
. (4.1.1)
Пространство элементарных исходов каждого отдельного испытания состоит из двух исходов 1 и 0. Очевидно, пространство элементарных исходов 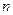 испытаний Бернулли содержит
испытаний Бернулли содержит 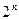 последовательностей из
последовательностей из 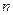 символов 1 и 0. Так как испытания независимы, то вероятности перемножаются, т. е. вероятность любой конкретной последовательности есть произведение, полученное при замене символов 1 и 0 вероятности на
символов 1 и 0. Так как испытания независимы, то вероятности перемножаются, т. е. вероятность любой конкретной последовательности есть произведение, полученное при замене символов 1 и 0 вероятности на  и
и  соответственно. Таким образом, вероятность исхода
соответственно. Таким образом, вероятность исхода 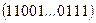 равна:
равна:
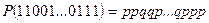 .
.
Но на практике нас, как правило, интересует не порядок появления успехов в последовательности 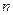 испытаний Бернулли, а их общее число.
испытаний Бернулли, а их общее число.
Теорема. Вероятность 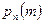 того, что в
того, что в 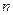 испытаниях Бернулли число успехов равно
испытаниях Бернулли число успехов равно 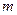 , вычисляется по формуле
, вычисляется по формуле
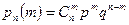 , (4.1.2)
, (4.1.2)
где  — вероятность «успеха», а
— вероятность «успеха», а  — вероятность «неудачи».
— вероятность «неудачи».
Доказательство. Событие «в 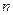 испытаниях Бернулли число успехов равно
испытаниях Бернулли число успехов равно 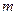 и число неудач —
и число неудач — 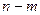 » содержит столько элементарных исходов, сколько существует способов размещения
» содержит столько элементарных исходов, сколько существует способов размещения 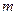 символов на
символов на 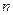 местах, т.е.
местах, т.е.  . А так как вероятность конкретной последовательности, содержащей
. А так как вероятность конкретной последовательности, содержащей 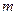 символов 1, равна
символов 1, равна 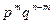 , то в итоге получаем:
, то в итоге получаем:
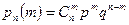 . n
. n
Число успехов в 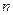 испытаниях обозначают через
испытаниях обозначают через 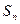 , тогда
, тогда 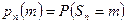 . Очевидно, что
. Очевидно, что 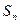 есть случайная величина, а функция (4.1.2) является «распределением» этой случайной величины. Будем называть это распределение биномиальным. Слово биномиальное отражает тот факт, что (4.1.2) представляет собой m-й член биноминального разложения
есть случайная величина, а функция (4.1.2) является «распределением» этой случайной величины. Будем называть это распределение биномиальным. Слово биномиальное отражает тот факт, что (4.1.2) представляет собой m-й член биноминального разложения 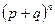 . Отсюда следует, что
. Отсюда следует, что
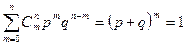 .
.
Пример 1. Стрелок попадает в мишень с вероятностью 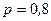 . Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает:
. Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает:
a) ровно четыре раза;
б) не менее трех раз.
m Решение. Для решения данной задачи применим формулу (4.1.2), в которой:
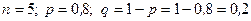 .
.
а) Число успехов равно 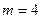 . Таким образом, искомая вероятность:
. Таким образом, искомая вероятность:
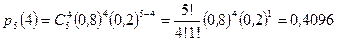 .
.
б) Обозначим 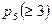 — вероятность попадания не менее трех раз из пяти.
— вероятность попадания не менее трех раз из пяти.
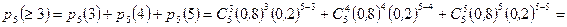
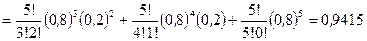 . l
. l
Пример 2. Сколько испытаний с вероятностью успеха 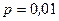 нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5?
нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5?
m Решение. Рассмотрим следующие события:
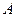 — в схеме Бернулли наблюдался хотя бы один успех;
— в схеме Бернулли наблюдался хотя бы один успех;
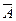 — в схеме Бернулли не наблюдалось ни одного успеха.
— в схеме Бернулли не наблюдалось ни одного успеха.
Для решения задачи используем формулу (4.1.2), согласно которой вероятность того, что успехов не будет (т.е. число успехов равно нулю), равна:
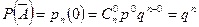 .
.
Используя свойство вероятности противоположного события, получаем, что вероятность того, что будет хотя бы один успех, равна:
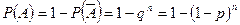 .
.
Остается найти наименьшее целое 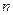 , для которого выполнено неравенство:
, для которого выполнено неравенство:
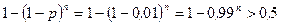 .
.
Решим последнее неравенство.
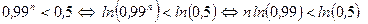 .
.
Разделив последнее неравенство на 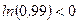 , получим
, получим
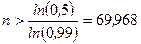 .
.
Наименьшим целым числом 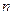 , удовлетворяющим последнему неравенству, является
, удовлетворяющим последнему неравенству, является 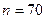 . l
. l
Пример 3. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен):
а) три партии из четырех или пять из восьми;
б) не менее трех партий из четырех или не менее пяти партий из восьми.
m Решение. Так как противники равносильны и ничейный исход партии исключен, то вероятности выигрыша и проигрыша каждой партии одинаковы и 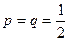 .
.
а) Вероятность выигрыша трех партий из четырех равна:
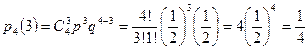 ,
,
а вероятность выигрыша пяти партий из восьми равна:
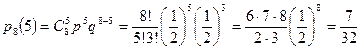 .
.
Так как 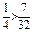 , то вероятнее выиграть три партии из четырех.
, то вероятнее выиграть три партии из четырех.
б) Вероятность выигрыша не менее трех партий из четырех равна:
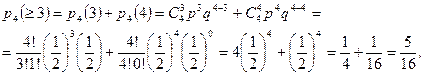
а вероятность выигрыша не менее пяти партий из восьми равна:
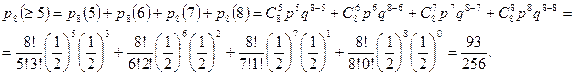
Так как 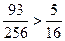 , то вероятнее выиграть не менее пяти партий из восьми. l
, то вероятнее выиграть не менее пяти партий из восьми. l
Формула Пуассона
При больших значениях числа испытаний 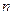 применение формулы Бернулли (4.1.2) затруднительно. Поэтому применяются простые, но достаточно точные приближенные формулы для вычисления
применение формулы Бернулли (4.1.2) затруднительно. Поэтому применяются простые, но достаточно точные приближенные формулы для вычисления 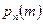 . Пусть число испытаний
. Пусть число испытаний 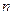 достаточно «велико», вероятность «успеха»
достаточно «велико», вероятность «успеха» 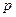 достаточно «мала». Пусть произведение
достаточно «мала». Пусть произведение
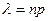 (4.2.1)
(4.2.1)
и не мало, и не велико. В таких случаях удобно использовать для вероятности 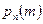 предложенное Пуассоном приближение (формула Пуассона), которое мы сейчас выведем. По формуле Бернулли (4.1.2)
предложенное Пуассоном приближение (формула Пуассона), которое мы сейчас выведем. По формуле Бернулли (4.1.2)
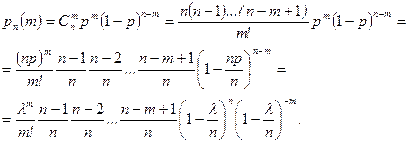 (4.2.2)
(4.2.2)
При 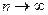 и сделанных выше допущениях очевидны следующие приближения:
и сделанных выше допущениях очевидны следующие приближения:
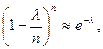
 ,
, 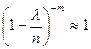 .
.
Следовательно, (4.2.2) примет вид:
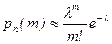 , (4.2.3)
, (4.2.3)
а это и есть формула Пуассона.
Замечание. При выводе формулы Пуассона (4.2.3) использовалось то, что 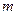 мало.
мало.
Замечание. Формула Пуассона (4.2.3) зависит от 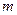 и
и 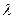 . Значения функции (4.2.2) можно определить следующими способами:
. Значения функции (4.2.2) можно определить следующими способами:
§ можно воспользоваться Приложением 1;
§ используя функцию ПУАССОН(x;среднее;интегральная) из EXCEL; в которой аргумент x равен числу «успехов» 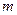 , аргумент «среднее» равен
, аргумент «среднее» равен 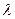 , аргумент «интегральная» должен равняться 0;
, аргумент «интегральная» должен равняться 0;
§ используя функцию dpois(k, l) из MATHCAD, в которой 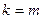 и
и 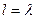 .
.
Пример 4. Найти вероятность того, что среди 1460 человек ровно трое родились 29 февраля.
m Решение. Вероятность того, что один конкретный человек родился 29 февраля, равна 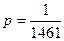 , т.к. 29 февраля бывает ровно 1 раз в 4 года.
, т.к. 29 февраля бывает ровно 1 раз в 4 года.
Далее находим коэффициент 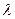 :
:
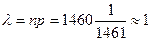 .
.
Применяя (4.2.2), получаем:
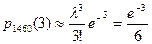 . l
. l
Пример 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность того, что при 5000 выстрелах в цель попало не менее двух выстрелов.
m Решение. Рассмотрим два противоположных события:
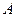 — при 5000 выстрелах в цель попало не менее двух выстрелов;
— при 5000 выстрелах в цель попало не менее двух выстрелов;
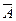 — при 5000 выстрелах в цель попало менее двух выстрелов.
— при 5000 выстрелах в цель попало менее двух выстрелов.
Найдем вероятность события 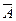 :
:
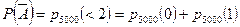 .
.
В рассматриваемом примере
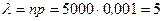 .
.
Используя формулу Пуассона, получим
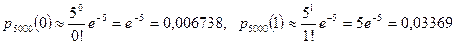 .
.
Используя свойство вероятности противоположного события, получим
 . l
. l
Формулы Муавра – Лапласа
Если в схеме Бернулли 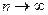 ,
, 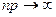 ,
,  , (4.3.1)
, (4.3.1)
то следует применять формулы Муавра – Лапласа: локальную или интегральную.
Локальная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли 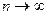 , то для всех
, то для всех 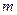 справедлива локальная формула Муавра‑Лапласа:
справедлива локальная формула Муавра‑Лапласа:
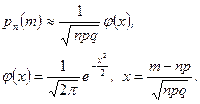 (4.3.2)
(4.3.2)
Значения функции 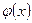 , которую называют плотностью нормального распределения с параметрами
, которую называют плотностью нормального распределения с параметрами 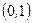 , можно найти одним из следующих способов:
, можно найти одним из следующих способов:
§ можно воспользоваться Приложением 2;
§ используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 0.
§ используя функцию dnorm(x, mu, sigma) из MATHCAD, в которой 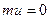 и
и 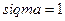 .
.
Очевидно, что функция 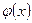 является четной. Поэтому при определении
является четной. Поэтому при определении 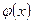 для отрицательных
для отрицательных 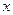 нужно воспользоваться равенством
нужно воспользоваться равенством 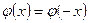 .
.
Интегральная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли число испытаний 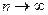 , то для вероятности
, то для вероятности 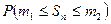 того, что число успехов
того, что число успехов 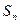 заключено в пределах от
заключено в пределах от 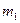 до
до 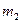 , справедлива интегральная теорема Муавра‑Лапласа:
, справедлива интегральная теорема Муавра‑Лапласа:
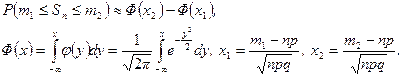 (4.3.3)
(4.3.3)
Функция 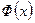 , определенная формулой (4.3.3), называется функцией распределения нормального распределения с параметрами
, определенная формулой (4.3.3), называется функцией распределения нормального распределения с параметрами 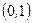 . Значения функции
. Значения функции 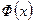 можно найти одним из следующих способов:
можно найти одним из следующих способов:
§ можно воспользоваться Приложением 3;
§ используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 1.
§ используя функцию pnorm(x, mu, sigma)из MATHCAD, в которой 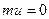 и
и 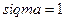 .
.
Функцию 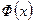 при отрицательных значениях переменной можно определить по формуле
при отрицательных значениях переменной можно определить по формуле 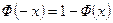 .
.
Замечание. Наряду с функцией 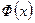 используют функцию
используют функцию
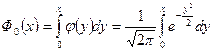 . (4.3.4)
. (4.3.4)
Для нее справедливо равенство 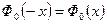 ; она связана с функцией
; она связана с функцией 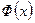 равенством
равенством
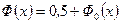 . (4.3.5)
. (4.3.5)
Пример 6. Симметричную монету бросают 400 раз. Определить вероятность появления герба:
а) от 185 до 210 раз;
б) ровно 200 раз;
в) не менее 200 раз.
m Решение. Для решения задачи применим локальную и интегральную теоремы Муавра‑Лапласа, для которых
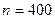 , т.к. монету подбрасывали 400 раз,
, т.к. монету подбрасывали 400 раз, 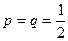 , т.к. монета симметрична.
, т.к. монета симметрична.
а) Используя интегральную теорему Муавра‑Лапласа, получим

б) Используя локальную теорему Муавра‑Лапласа, получим
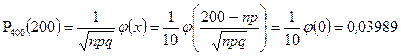 ;
;
в) Используя интегральную теорему Муавра‑Лапласа, получим
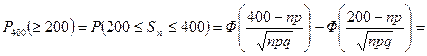
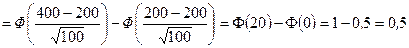 . l
. l
Пример 7. Команда состоит из 10 отличных и 15 хороших стрелков. Каждый стрелок производит по своей мишени 5 независимых выстрелов. Отличный стрелок при каждом выстреле попадает в цель с вероятностью 0,9, хороший — с вероятностью 0,8. Определить вероятность того, что общее число попаданий будет не менее 110.
m Решение. Найдем вероятность попадания при одном выстреле для произвольного стрелка. Для этого воспользуемся формулой полной вероятности. Пусть искомое событие 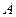 — мишень поражена одним стрелком. Рассмотрим следующие гипотезы:
— мишень поражена одним стрелком. Рассмотрим следующие гипотезы:
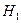 — стреляет отличный стрелок;
— стреляет отличный стрелок;
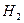 — стреляет хороший стрелок.
— стреляет хороший стрелок.
Очевидно, что:
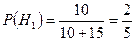 ,
, 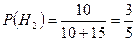 ,
, 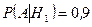 ,
, 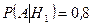 .
.
Отсюда получаем:
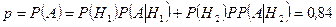 ,
, 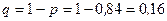 .
.
Заметим, что общее число выстрелов
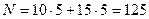 .
.
Теперь найдем вероятность 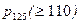 того, что при 125 выстрелах число попаданий будет не менее 110. Для этого применим интегральную теорему Муавра‑Лапласа:
того, что при 125 выстрелах число попаданий будет не менее 110. Для этого применим интегральную теорему Муавра‑Лапласа:
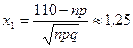 ,
, 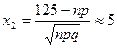 ,
,
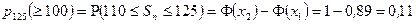 . l
. l
Пример 8. Вероятность попадания в мишень при одном выстреле  . Найти наименьшее число выстрелов, которое надо произвести по мишени, чтобы с вероятностью 0,95 число попаданий было не менее 70.
. Найти наименьшее число выстрелов, которое надо произвести по мишени, чтобы с вероятностью 0,95 число попаданий было не менее 70.
m Решение. По условию задачи 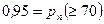 . Для вычисления
. Для вычисления 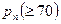 применим интегральную теорему Муавра – Лапласа:
применим интегральную теорему Муавра – Лапласа:
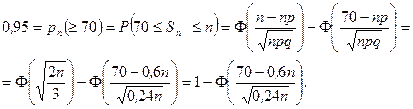
Заметим, что мы использовали то, что при больших значениях 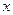
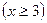
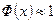 .
.
Далее получаем
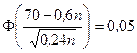 .
.
Используя Приложение 3 находим, что
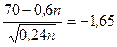 .
.
Решая последнее уравнение для натуральных значений 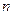 , получаем, что n=132 . l
, получаем, что n=132 . l
Понятие случайной величины
Определение. Случайной величиной 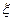 называется функция, ставящая в соответствие каждому элементарному исходу
называется функция, ставящая в соответствие каждому элементарному исходу 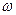 число
число 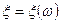 .
.
Пример 1. Рассмотрим схему Бернулли с вероятностью успеха 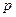 . Сопоставим каждому элементарному исходу
. Сопоставим каждому элементарному исходу 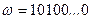 функцию
функцию 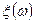 , равную числу успехов данного исхода, т.е. числу символов 1, содержащихся в последовательности
, равную числу успехов данного исхода, т.е. числу символов 1, содержащихся в последовательности  .
.
Пример 2. Случайными величинами является число очков при бросании игральной кости, сумма очков при бросании нескольких игральных костей.
Пример 3. Случайной величиной является координата точки, упавшей на отрезок 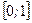 . В этом случае
. В этом случае 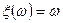 .
.
В общем случае случайные величины делятся на дискретные и непрерывные.
Определение. Дискретной называется случайная величина, которая каждому элементарному исходу 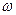 ставит в соответствие одно из конечного (или в общем случае счетного) набора чисел
ставит в соответствие одно из конечного (или в общем случае счетного) набора чисел 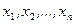
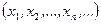 .
.
Определение. Непрерывной называется случайная величина, возможные значения которой непрерывно заполняют некоторую область.
Однако существуют случайные величины, не относящиеся ни к одному из этих типов. Простейшим примером такой случайной величины является время работы электроприбора. Купленный электроприбор может с ненулевой вероятностью оказаться бракованным, т.е. время его работы будет равно 0, и в этом смысле необходимо считать рассматриваемую случайную величину дискретной. Если же прибор окажется исправным, то время его работы необходимо считать непрерывной случайной величиной.
Основные понятия и основные задачи математической статистики
В математической статистике исследуются способы получения выводов на основе эмпирических (опытных) данных. Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.
Определение. Генеральной совокупностью называются все возможные результаты наблюдений, которые могут быть сделаны при данном комплексе условий.
В некоторых задачах генеральную совокупность рассматривают как случайную величину 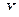 . Примером генеральной совокупности может быть все население страны. В этой совокупности нас могут интересовать, например, возраст жителей. Другим примером генеральной совокупности являются детали, изготовленные на данном станке. Эти детали могут быть качественными и бракованными.
. Примером генеральной совокупности может быть все население страны. В этой совокупности нас могут интересовать, например, возраст жителей. Другим примером генеральной совокупности являются детали, изготовленные на данном станке. Эти детали могут быть качественными и бракованными.
Определение. Выборочной совокупностью (выборкой) называется множество результатов, случайно отобранных из генеральной совокупности.
Выборка должна быть репрезентативной, т.е. правильно отражать пропорции генеральной совокупности. Это достигается случайностью отбора, когда все объекты генеральной совокупности имеют одинаковую вероятность быть отобранными.
Определение. Число объектов в совокупности (генеральной или выборочной) называется ее объемом.
Объем генеральной совокупности обозначим символом 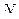 , а объем выборочной совокупности обозначим символом
, а объем выборочной совокупности обозначим символом  . При этом подразумевается, что
. При этом подразумевается, что 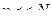 .
.
Заметим, что сам процесс выбора можно осуществлять разными способами: выбрав объект и определив его значение, изымать объект и не допускать к последующим испытаниям (выборка без возвращения); после определения его значения объект возвращается в генеральную совокупность (выборка с возвращением). Очевидно, что при достаточно большом объеме генеральной совокупности исчезает различие между выборками с возвращением и без возвращения. Будем рассматривать случай бесконечно большого объема генеральной совокупности.
Основные задачи математической статистики:
1. Оценка значения неизвестной вероятности случайного события;
2. Определение неизвестной теоретической функции распределения;
3. Определение неизвестных параметров распределения теоретической функции распределения;
4. Проверка статистических гипотез;
5. Оценка зависимости.
§2. Простейшие статистические преобразования
Для обоснованных статистических выводов необходимо иметь выборку достаточно большого объема  . Очевидно, что использование и хранение такой выборки весьма затруднительно. Чтобы избавиться от данных проблем, используют понятие статистики.
. Очевидно, что использование и хранение такой выборки весьма затруднительно. Чтобы избавиться от данных проблем, используют понятие статистики.
Определение. Статистикой 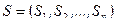 называется произвольная k‑мерная функция от выборки
называется произвольная k‑мерная функция от выборки 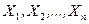 :
:
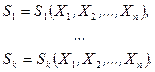
Как функция от случайного вектора 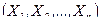 статистика
статистика 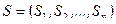 также будет случайным вектором.
также будет случайным вектором.
Определение. Вариационным рядом 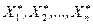 является выборка
является выборка 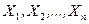 , элементы которой расположены в порядке возрастания элементов:
, элементы которой расположены в порядке возрастания элементов: 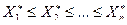 .
.
Очевидно, что данное преобразование не приводит к потере информации относительно теоретической функции распределения.
Для величин 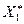 и
и 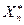 употребляют название «крайние члены вариационного ряда».
употребляют название «крайние члены вариационного ряда».
Определение. Размахом варьирования называется разность между крайними членами вариационного ряда, т.е.
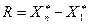 . (7.2.1)
. (7.2.1)
Если среди элементов выборки 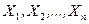 имеются одинаковые, что происходит при наблюдении дискретной случайной величины, то целесообразно произвести группировку данных.
имеются одинаковые, что происходит при наблюдении дискретной случайной величины, то целесообразно произвести группировку данных.
Определение. Значение выборки 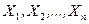 , соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантой, а численность отдельной группы сгруппированного ряда наблюдаемых данных, называется частотой или весом варианты.
, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантой, а численность отдельной группы сгруппированного ряда наблюдаемых данных, называется частотой или весом варианты.
Если 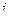 — индекс варианты, то
— индекс варианты, то 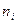 — число значений
— число значений 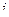 ‑ой варианты.
‑ой варианты.
Определение. Отношение частоты 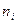 к общей сумме всех частот
к общей сумме всех частот 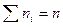 называется относительной частотой варианты и обозначается
называется относительной частотой варианты и обозначается 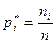 .
.
Определение. Статистическим рядом называется расположенная по возрастанию совокупность различных вариант 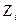 , представляющих выборку
, представляющих выборку 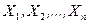 , с соответствующими им частотами или относительными частотами.
, с соответствующими им частотами или относительными частотами.
При наблюдении непрерывной случайной величины используют интервальный ряд. В этом случае весь возможный интервал, которому принадлежат значения выборки, разбивают на конечное число частичных интервалов и подсчитывают частоту попадания элементов выборки в каждый частичный интервал.
Определение. Интервальным рядом называется упорядоченная последовательность интервалов с соответствующими им частотами или относительными частотами попадания элементов выборки в каждый из этих интервалов.
Пример 1. В городе A для определения сроков гарантированного обслуживания проведено исследование величины среднего пробега автомобилей, находящихся в эксплуатации в течение двух лет. Получены следующие результаты (тыс. км.):
3,0; 25,0; 18,6; 12,1; 10,6; 18,0; 17,3; 29,1; 20,0; 18,3; 21,5; 26,7; 12,2; 14,4; 7,3; 9,1; 2,9; 5,4; 40,1; 16,8; 11,2; 9,9; 25,3; 4,2; 29,6.
Составить интервальный ряд.
m Решение. Очевидно, что величина среднего пробега автомобилей, находящихся в эксплуатации в течение двух лет, является непрерывной случайной величиной. Полученные данные представляют собой выборку из 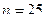 наблюдений. Найдем сначала минимальное и максимальное значения случайной величины (т.е. крайние члены вариационного ряда):
наблюдений. Найдем сначала минимальное и максимальное значения случайной величины (т.е. крайние члены вариационного ряда): 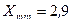 и
и 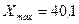 . Размах варьирования будет равен
. Размах варьирования будет равен 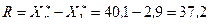 .
.
Возьмем число частичных интервалов 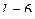 . В этом случае длина частичного интервала равна
. В этом случае длина частичного интервала равна
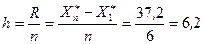 .
.
Соответствующий интервальный ряд приведен в таблице 7.1.
Таблица 7.1
Номер
интервала
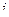
| Средний пробег автомобилей
(интервалы)
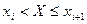
| Частота
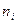
| Относительная частота
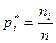
|
| 1 | 2,9 — 9,1 | 6 | 0,24 |
| 2 | 9,1 — 15,3 | 6 | 0,24 |
| 3 | 15,3 — 21,5 | 7 | 0,28 |
| 4 | 21,5 — 27,7 | 3 | 0,12 |
| 5 | 27,7 — 33,9 | 2 | 0,08 |
| 6 | 33,9 — 40,1 | 1 | 0,04 |
l
Пример 2. Наблюдается число выигрышей в мгновенной лотерее. В результате наблюдения получены следующие значения выигрышей (тыс. руб.):
0, 1, 0, 0, 5, 0, 10, 0, 1, 0, 0, 1, 5, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 5, 0, 5, 0, 0, 1, 1, 1, 5, 10, 0, 1, 1, 0, 5, 0, 0, 0, 0, 1, 0, 1, 0, 5, 0, 0, 0, 0, 1, 0.
Требуется составить статистический ряд случайной величины 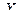 — выигрыша в мгновенной лотерее.
— выигрыша в мгновенной лотерее.
m Решение. Случайная величина 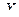 принимает 4 различных значения: 0, 1, 5 и 10. Для каждого значения подсчитаем частоту и относительную частоту. Результаты задачи представим в таблице 7.2.
принимает 4 различных значения: 0, 1, 5 и 10. Для каждого значения подсчитаем частоту и относительную частоту. Результаты задачи представим в таблице 7.2.
Таблица 7.2
| № |
| 1 | 2 | 3 | 4 |
| Выигрыш в мгновенной лотерее | 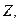
| 0 | 1 | 5 | 10 |
| Частота | | 31 | 14 | 7 | 2 |
| Относительная частота | 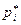
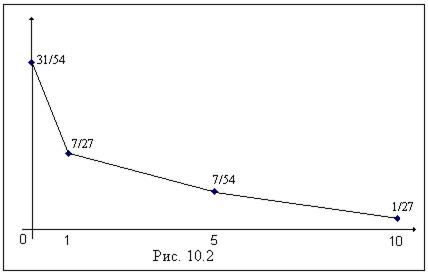
| 31/54 | 7/27 | 7/54 | 1/27 |
l
Полигон и гистограмма
Определение. Полигоном частот (многоугольником распределения) называется ломаная линия, проходящая через точки с координатами 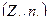 , где
, где 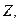 — варианты статистического ряда, а
— варианты статистического ряда, а 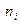 — соответствующие им частоты.
— соответствующие им частоты.
Если ломаная линия строится по точкам 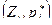 , где
, где 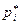 — относительные частоты, то получаем полигон относительных частот.
— относительные частоты, то получаем полигон относительных частот.
Построим полигон относительных частот для выборки из примера 2. Используя статистический ряд, представленный в таблице 7.2, получаем полигон относительных частот, изображенный на рис. 7.2.
В случае непрерывной случайной величины выборку преобразуют следующим образом. Всю ось абсцисс делят на интервалы 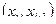 длины
длины 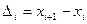 и определяют функцию
и определяют функцию 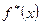 , которая на
, которая на 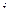 ‑м интервале принимает значение
‑м интервале принимает значение
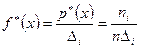 , (7.4.1)
, (7.4.1)
где 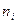 — число элементов выборки, попавших в интервал.
— число элементов выборки, попавших в интервал.
Определение. Функция 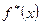 , определенная соотношением (7.4.1), называется гистограммой.
, определенная соотношением (7.4.1), называется гистограммой.
Гистограмма является выборочной оценкой плотности вероятности.
Построим гистограмму по данным, приведенным в примере 1. Длина каждого интервала равна 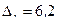 . Подсчитаем значения
. Подсчитаем значения 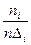 :
:
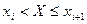
| 2,9 — 9,1 | 9,1 — 15,3 | 15,3—21,5 | 21,5—27,7 | 27,7—33,9 | 33,9—40,1 |
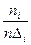
| 0,038710 | 0,038710 | 0,045161 | 0,019355 | 0,012903 | 0,006452 |
На рис. 7.3 представлена гистограмма примера 1.
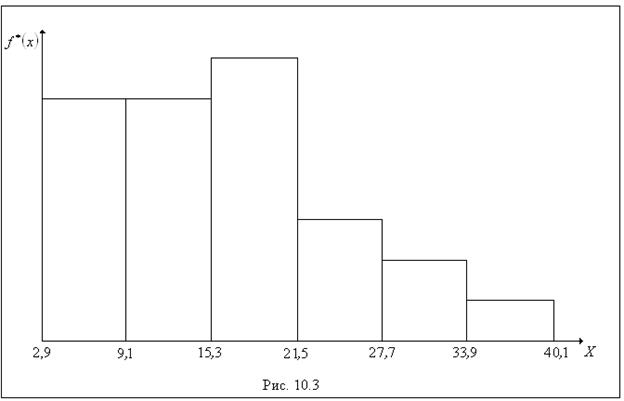
Графическое изображение статистических рядов в виде полигона и гистограммы позволяет получить первоначальное представление о закономерностях, имеющих место в совокупности наблюдений.
M Решение.
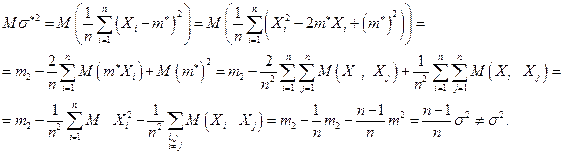
Таким образом, 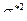 является смещенной оценкой дисперсии
является смещенной оценкой дисперсии 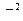 . Очевидно, что
. Очевидно, что 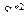 будет уже несмещенной оценкой дисперсии
будет уже несмещенной оценкой дисперсии 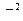 . l
. l
Метод моментов
Пусть имеется выборка 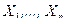 , произведенная из генеральной совокупности с теоретической функцией распределения
, произведенная из генеральной совокупности с теоретической функцией распределения 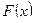 , зависящей от
, зависящей от 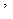 параметров
параметров 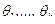 , которые нужно оценить. Зная функцию распределения, можно найти первые
, которые нужно оценить. Зная функцию распределения, можно найти первые 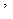 теоретических моментов, которые будут зависеть от параметров
теоретических моментов, которые будут зависеть от параметров 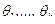 :
:
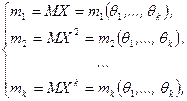 (8.2.1)
(8.2.1)
где 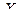 — случайная величина, имеющая функцию распределения
— случайная величина, имеющая функцию распределения 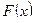 .
.
Метод моментов состоит в том, что в системе (8.2.1) при большом объёме выборки 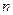 теоретические моменты
теоретические моменты 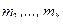 заменяются на выборочные
заменяются на выборочные 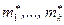 , а затем, решая эту систему относительно
, а затем, решая эту систему относительно 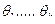 , находят оценки неизвестных параметров. Таким образом, в методе моментов оценки
, находят оценки неизвестных параметров. Таким образом, в методе моментов оценки 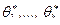 неизвестных параметров
неизвестных параметров 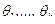 определяются из системы уравнений
определяются из системы уравнений
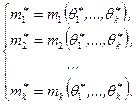 (8.2.2)
(8.2.2)
Метод моментов был предложен в 1894 г. К. Пирсоном. Оценки, полученные методом моментов, как правило, являются состоятельными.
Пример 3. Выборка 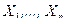 произведена из генеральной совокупности с теоретической функцией распределения, имеющей плотность показательного закона
произведена из генеральной совокупности с теоретической функцией распределения, имеющей плотность показательного закона
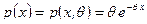
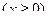
Найти оценку параметра 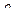 .
.
m Решение. Математическое ожидание случайной величины 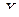 , имеющей плотность показательного закона, задаётся формулой
, имеющей плотность показательного закона, задаётся формулой
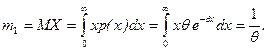
Используя систему (8.2.2), получаем 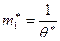 .
.
Откуда окончательно получаем 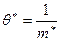 . l
. l
Доказательство.
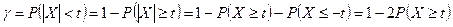 ,
,
т.к. ввиду симметричности закона распределения относительно оси 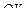 выполнено равенство
выполнено равенство  . Отсюда следует, что
. Отсюда следует, что
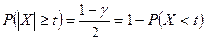 и
и 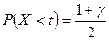 . n
. n
Рассмотрим теперь правила построения доверительных интервалов для некоторых параметров распределения.
Основные понятия
Определение. Статистической гипотезой называется любое предположение 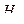 (гипотеза) о виде закона распределения генеральной совокупности или о числовых значениях параметров закона распределения.
(гипотеза) о виде закона распределения генеральной совокупности или о числовых значениях параметров закона распределения.
Определение. Правило, по которому гипотеза 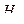 принимается или отвергается, называется статистическим критерием.
принимается или отвергается, называется статистическим критерием.
Проверяемую гипотезу 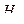 называют нулевой, а противоположную ей гипотезу
называют нулевой, а противоположную ей гипотезу 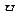 называют альтернативной.
называют альтернативной.
Схема проверки нулевой гипотезы:
1. Используя проверочные данные 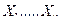 и учитывая условия задачи, принимают нулевую гипотезу
и учитывая условия задачи, принимают нулевую гипотезу 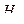 и альтернативную гипотезу
и альтернативную гипотезу 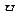 .
.
2. По случайной выборке 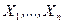 определяется функция
определяется функция 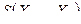 , называемая статистикой, для которой будет известен точный или приближённый закон распределения.
, называемая статистикой, для которой будет известен точный или приближённый закон распределения.
3. По заранее выбранной малой вероятности 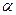 определяется критическая область
определяется критическая область 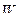 , для которой
, для которой 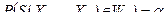 . И если величина
. И если величина  , вычисляется при конкретной выборке
, вычисляется при конкретной выборке 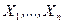 , окажется вне критической области
, окажется вне критической области 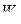 , то гипотеза
, то гипотеза 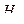 принимается, а если она окажется в области
принимается, а если она окажется в области 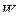 , то гипотеза
, то гипотеза 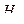 отвергается (или принимается гипотеза
отвергается (или принимается гипотеза 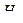 ). При этом возможны 4 случая, которые представлены в таблице 9.1
). При этом возможны 4 случая, которые представлены в таблице 9.1
Таблица 9.1
Принимается 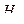
| Отвергается 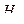
| |
Верна гипотеза 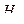
| Правильное решение | Ошибка первого рода |
| вероятность | 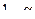
| 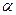
|
Верна 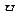
| Ошибка второго рода | Правильное решение |
| вероятность | 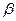
| 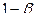
|
Определение. Вероятность 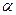 допустить ошибку первого рода называется уровнем значимости критерия.
допустить ошибку первого рода называется уровнем значимости критерия.
Определение. Вероятность 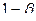 не допустить ошибку второго рода называется мощностью критерия.
не допустить ошибку второго рода называется мощностью критерия.
Если использовать терминологию качества продукции, то 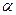 — это «риск поставщика», связанный с забраковкой по результату выборки всей партии товара, соответствующей стандарту, а
— это «риск поставщика», связанный с забраковкой по результату выборки всей партии товара, соответствующей стандарту, а 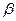 — «риск потребителя», связанный с принятием по результатам выборки партии товара, не соответствующей стандарту.
— «риск потребителя», связанный с принятием по результатам выборки партии товара, не соответствующей стандарту.
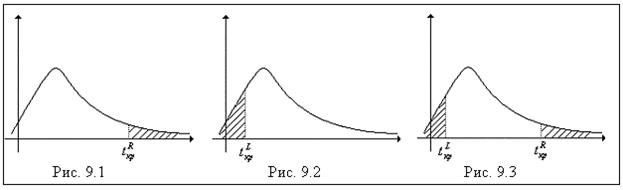
Возможны три варианта расположения критической области:
1. Правосторонняя критическая область (рис 9.1), состоящая из интервала 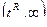 , где
, где 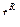 определяется из условия:
определяется из условия:
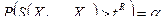 . (9.1.1)
. (9.1.1)
2. Левосторонняя критическая область (рис 9.2), состоящая из интервала 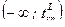 , где
, где 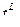 определяется из условия:
определяется из условия:
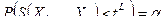 . (9.1.2)
. (9.1.2)
3. Двусторонняя критическая область (рис 9.3), состоящая из интервалов 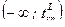 и
и 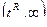 , где точки
, где точки 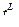 и
и 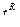 определяется из условий:
определяется из условий:
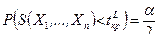 и
и 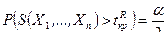 . (9.1.3)
. (9.1.3)
В следующих параграфах рассмотрим несколько конкретных практических примеров.
Приложения
Приложение 1
Таблица значений функции 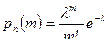
| m | Значения | ||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | |
| 0 | 0,904837 | 0,818731 | 0,740818 | 0,670320 | 0,606531 | 0,548812 | 0,496585 |
| 1 | 0,090484 | 0,163746 | 0,222245 | 0,268128 | 0,303265 | 0,329287 | 0,347610 |
| 2 | 0,004524 | 0,016375 | 0,033337 | 0,053626 | 0,075816 | 0,098786 | 0,121663 |
| 3 | 0,000151 | 0,001092 | 0,003334 | 0,007150 | 0,012636 | 0,019757 | 0,028388 |
| 4 | 0,000004 | 0,000055 | 0,000250 | 0,000715 | 0,001580 | 0,002964 | 0,004968 |
| 5 |
| 0,000002 | 0,000015 | 0,000057 | 0,000158 | 0,000356 | 0,000696 |
| 6 |
|
| 0,000001 | 0,000004 | 0,000013 | 0,000036 | 0,000081 |
| 7 |
|
|
|
| 0,000001 | 0,000003 | 0,000008 |
| 8 |
|
|
|
|
|
| 0,000001 |
| m | Значения | ||||||
| 0,8 | 0,9 | 1 | 2 | 3 | 4 | 5 | |
| 0 | 0,449329 | 0,406570 | 0,367879 | 0,135335 | 0,049787 | 0,018316 | 0,006738 |
| 1 | 0,359463 | 0,365913 | 0,367879 | 0,270671 | 0,149361 | 0,073263 | 0,033690 |
| 2 | 0,143785 | 0,164661 | 0,183940 | 0,270671 | 0,224042 | 0,146525 | 0,084224 |
| 3 | 0,038343 | 0,049398 | 0,061313 | 0,180447 | 0,224042 | 0,195367 | 0,140374 |
| 4 | 0,007669 | 0,011115 | 0,015328 | 0,090224 | 0,168031 | 0,195367 | 0,175467 |
| 5 | 0,001227 | 0,002001 | 0,003066 | 0,036089 | 0,100819 | 0,156293 | 0,175467 |
| 6 | 0,000164 | 0,000300 | 0,000511 | 0,012030 | 0,050409 | 0,104196 | 0,146223 |
| 7 | 0,000019 | 0,000039 | 0,000073 | 0,003437 | 0,021604 | 0,059540 | 0,104445 |
| 8 | 0,000002 | 0,000004 | 0,000009 | 0,000859 | 0,008102 | 0,029770 | 0,065278 |
| 9 |
|
| 0,000001 | 0,000191 | 0,002701 | 0,013231 | 0,036266 |
| 10 |
|
|
| 0,000038 | 0,000810 | 0,005292 | 0,018133 |
| 11 |
|
|
| 0,000007 | 0,000221 | 0,001925 | 0,008242 |
| 12 |
|
|
| 0,000001 | 0,000055 | 0,000642 | 0,003434 |
| 13 |
|
|
|
| 0,000013 | 0,000197 | 0,001321 |
| 14 |
|
|
|
| 0,000003 | 0,000056 | 0,000472 |
| 15 |
|
|
|
| 0,000001 | 0,000015 | 0,000157 |
| 16 |
|
|
|
|
| 0,000004 | 0,000049 |
| 17 |
|
|
|
|
| 0,000001 | 0,000014 |
| 18 |
|
|
|
|
|
| 0,000004 |
| 19 |
|
|
|
|
|
| 0,000001 |
Приложение 2
Приложение 3
Приложение 4
Критические точки распределения 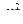
| Число степеней свободы | Уровень значимости α | |||||||||
| 0,01 | 0,025 | 0,05 | 0,075 | 0,1 | 0,9 | 0,925 | 0,95 | 0,975 | 0,99 | |
| 1 | 6,63 | 5,02 | 3,84 | 3,17 | 2,71 | 0,02 | 0,01 | 0,00 | 0,00 | 0,00 |
| 2 | 9,21 | 7,38 | 5,99 | 5,18 | 4,61 | 0,21 | 0,16 | 0,10 | 0,05 | 0,02 |
| 3 | 11,34 | 9,35 | 7,81 | 6,90 | 6,25 | 0,58 | 0,47 | 0,35 | 0,22 | 0,11 |
| 4 | 13,28 | 11,14 | 9,49 | 8,50 | 7,78 | 1,06 | 0,90 | 0,71 | 0,48 | 0,30 |
| 5 | 15,09 | 12,83 | 11,07 | 10,01 | 9,24 | 1,61 | 1,39 | 1,15 | 0,83 | 0,55 |
| 6 | 16,81 | 14,45 | 12,59 | 11,47 | 10,64 | 2,20 | 1,94 | 1,64 | 1,24 | 0,87 |
| 7 | 18,48 | 16,01 | 14,07 | 12,88 | 12,02 | 2,83 | 2,53 | 2,17 | 1,69 | 1,24 |
| 8 | 20,09 | 17,53 | 15,51 | 14,27 | 13,36 | 3,49 | 3,14 | 2,73 | 2,18 | 1,65 |
| 9 | 21,67 | 19,02 | 16,92 | 15,63 | 14,68 | 4,17 | 3,78 | 3,33 | 2,70 | 2,09 |
| 10 | 23,21 | 20,48 | 18,31 | 16,97 | 15,99 | 4,87 | 4,45 | 3,94 | 3,25 | 2,56 |
| 11 | 24,73 | 21,92 | 19,68 | 18,29 | 17,28 | 5,58 | 5,12 | 4,57 | 3,82 | 3,05 |
| 12 | 26,22 | 23,34 | 21,03 | 19,60 | 18,55 | 6,30 | 5,82 | 5,23 | 4,40 | 3,57 |
| 13 | 27,69 | 24,74 | 22,36 | 20,90 | 19,81 | 7,04 | 6,52 | 5,89 | 5,01 | 4,11 |
| 14 | 29,14 | 26,12 | 23,68 | 22,18 | 21,06 | 7,79 | 7,24 | 6,57 | 5,63 | 4,66 |
| 15 | 30,58 | 27,49 | 25,00 | 23,45 | 22,31 | 8,55 | 7,97 | 7,26 | 6,26 | 5,23 |
| 16 | 32,00 | 28,85 | 26,30 | 24,72 | 23,54 | 9,31 | 8,71 | 7,96 | 6,91 | 5,81 |
| 17 | 33,41 | 30,19 | 27,59 | 25,97 | 24,77 | 10,09 | 9,45 | 8,67 | 7,56 | 6,41 |
| 18 | 34,81 | 31,53 | 28,87 | 27,22 | 25,99 | 10,86 | 10,21 | 9,39 | 8,23 | 7,01 |
| 19 | 36,19 | 32,85 | 30,14 | 28,46 | 27,20 | 11,65 | 10,97 | 10,12 | 8,91 | 7,63 |
| 20 | 37,57 | 34,17 | 31,41 | 29,69 | 28,41 | 12,44 | 11,73 | 10,85 | 9,59 | 8,26 |
| 21 | 38,93 | 35,48 | 32,67 | 30,92 | 29,62 | 13,24 | 12,50 | 11,59 | 10,28 | 8,90 |
| 22 | 40,29 | 36,78 | 33,92 | 32,14 | 30,81 | 14,04 | 13,28 | 12,34 | 10,98 | 9,54 |
| 23 | 41,64 | 38,08 | 35,17 | 33,36 | 32,01 | 14,85 | 14,06 | 13,09 | 11,69 | 10,20 |
| 24 | 42,98 | 39,36 | 36,42 | 34,57 | 33,20 | 15,66 | 14,85 | 13,85 | 12,40 | 10,86 |
| 25 | 44,31 | 40,65 | 37,65 | 35,78 | 34,38 | 16,47 | 15,64 | 14,61 | 13,12 | 11,52 |
| 26 | 45,64 | 41,92 | 38,89 | 36,98 | 35,56 | 17,29 | 16,44 | 15,38 | 13,84 | 12,20 |
| 27 | 46,96 | 43,19 | 40,11 | 38,18 | 36,74 | 18,11 | 17,24 | 16,15 | 14,57 | 12,88 |
| 28 | 48,28 | 44,46 | 41,34 | 39,38 | 37,92 | 18,94 | 18,05 | 16,93 | 15,31 | 13,56 |
| 29 | 49,59 | 45,72 | 42,56 | 40,57 | 39,09 | 19,77 | 18,85 | 17,71 | 16,05 | 14,26 |
| 30 | 50,89 | 46,98 | 43,77 | 41,76 | 40,26 | 20,60 | 19,66 | 18,49 | 16,79 | 14,95 |
| 31 | 52,19 | 48,23 | 44,99 | 42,95 | 41,42 | 21,43 | 20,48 | 19,28 | 17,54 | 15,66 |
| 32 | 53,49 | 49,48 | 46,19 | 44,13 | 42,58 | 22,27 | 21,30 | 20,07 | 18,29 | 16,36 |
| 33 | 54,78 | 50,73 | 47,40 | 45,31 | 43,75 | 23,11 | 22,12 | 20,87 | 19,05 | 17,07 |
| 34 | 56,06 | 51,97 | 48,60 | 46,49 | 44,90 | 23,95 | 22,94 | 21,66 | 19,81 | 17,79 |
| 35 | 57,34 | 53,20 | 49,80 | 47,66 | 46,06 | 24,80 | 23,76 | 22,47 | 20,57 | 18,51 |
| 36 | 58,62 | 54,44 | 51,00 | 48,84 | 47,21 | 25,64 | 24,59 | 23,27 | 21,34 | 19,23 |
| 37 | 59,89 | 55,67 | 52,19 | 50,01 | 48,36 | 26,49 | 25,42 | 24,07 | 22,11 | 19,96 |
| 38 | 61,16 | 56,90 | 53,38 | 51,17 | 49,51 | 27,34 | 26,25 | 24,88 | 22,88 | 20,69 |
| 39 | 62,43 | 58,12 | 54,57 | 52,34 | 50,66 | 28,20 | 27,09 | 25,70 | 23,65 | 21,43 |
| 40 | 63,69 | 59,34 | 55,76 | 53,50 | 51,81 | 29,05 | 27,93 | 26,51 | 24,43 | 22,16 |
| 99 | 134,64 | 128,42 | 123,23 | 119,91 | 117,41 | 81,45 | 79,51 | 77,05 | 73,36 | 69,23 |
| 100 | 135,81 | 129,56 | 124,34 | 121,02 | 118,50 | 82,36 | 80,41 | 77,93 | 74,22 | 70,06 |
Приложение 5
Оглавление
Глава 1. Случайные события и их вероятности. 2
§1. События. Действия с событиями. 2
§2. Общее определение и свойства вероятности. 4
ГЛАВА 2. Классическая и геометрическая вероятности. 5
§1. Классическое определение вероятности. 5
§2. Применение комбинаторного анализа. 9
§3. Геометрическое определение вероятности. 11
Глава 3. Условная вероятность. Независимость событий. Формулы полной вероятности и Байеса 14
§1. Условная вероятность. 14
§2. Теоремы сложения и умножения вероятностей. 15
§3. Независимость событий. 18
§4. Формула полной вероятности. 19
§5. Формула Байеса. 21
Глава 4. Схема независимых испытаний. Схема Бернулли. 24
§1. Формула Бернулли. 24
§2. Формула Пуассона. 26
§3. Формулы Муавра – Лапласа. 27
Глава 5. Случайные величины и их распределения. 30
§1. Понятие случайной величины.. 30
§2. Функция распределения случайной величины.. 30
§3. Дискретные случайные величины.. 31
§4. Непрерывные случайные величины.. 33
§5. Функция от случайных величин. 37
Глава 6. Числовые характеристики случайных величин. 41
§1. Математическое ожидание случайной величины.. 41
§2. Математическое ожидание функции от случайной величины. Свойства математического ожидания. 43
§3. Дисперсия. Моменты высших порядков. 47
Глава 7. Элементы математической статистики. 50
§1. Основные понятия и основные задачи математической статистики. 50
§2. Простейшие статистические преобразования. 50
§3. Эмпирическая функция распределения. 52
§4. Полигон и гистограмма. 54
Глава 8. Статистическое оценивание. 56
§1. Точечные оценки. Выборочная средняя и выборочная дисперсия. 56
§2. Метод моментов. 57
§3. Метод максимального правдоподобия. 58
§4. Интервальные оценки (доверительные интервалы) 59
Глава 9. Проверка статистических гипотез. 65
§1. Основные понятия. 65
§2. Проверка гипотезы о значении математического ожидания. 66
§3. Проверка гипотезы о равенстве математических ожиданий двух генеральных совокупностей 67
§4. Проверка гипотезы о значении дисперсии генеральной совокупности. 69
§5. Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей. 70
§6. Проверка гипотезы о распределении. Критерий Пирсона. 72
Приложения. 78
Используемая литература. 83
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
 |
Московский государственный университет
приборостроения и информатики

Кафедра высшей математики
Манжиров А.В., Михин М.Н.
Дата: 2019-02-25, просмотров: 322.