Рассмотрим основные операции над событиями; они полностью соответствуют основным операциям над множествами.

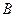Определение. Суммой событий  и  называется событие 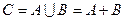, состоящее в наступлении хотя бы одного из событий  или .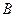

Определение. Произведением событий  и 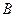 называется событие 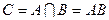, состоящее в совместном (одновременном) наступлении этих событий.

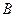Определение. Разностью событий  и  называется событие 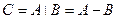, состоящее в том, что событие  произошло, а событие 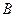 не произошло.

Определение. Событие, состоящее в том, что событие  не происходит, называется противоположным событию  и обозначается .

Определение. Событие  влечет событие 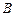 (  является подмножеством множества 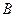), если из того, что происходит событие , следует, что происходит событие 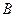; записывают .

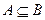Определение. Если одновременно 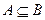 и 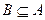, то в этом случае события  и 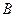 называют равносильными, при этом пишут .

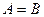Пример 4. Если  — событие, состоящее в том, что взятое наудачу изделие первого сорта, а 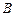 — изделие качественное (не брак), то в том событие  влечет событие : .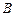

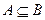Свойства операций над событиями:

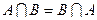§ ,  (коммутативность);

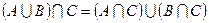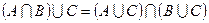§ ,  (дистрибутивность);

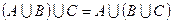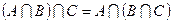§ ,  (ассоциативность);

§ , ;

§ , ;

§ , ;

§ , , ;

§ ;

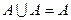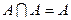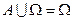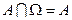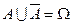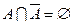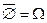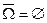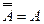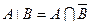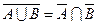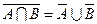§ ,  (законы де Моргана).

Определение. События 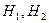 называют несовместными, если при наступлении одного из событий, второе событие в данном испытании наступить уже не может.

Так, например, если при бросании игральной кости выпала грань «2», то это означает, что при том же бросании не могла появиться грань «4».

Определение. События 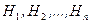 образуют полную группу событий, если в результате опыта, одно из событий обязательно происходит.

Например, при однократном бросании игральной кости полная группа попарно несовместных событий состоит из событий

,

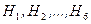которые состоят в выпадении 1,2,3,4,5,6 очков, соответственно.

Определение. Полная группа попарно несовместных, равновозможных событий образует множество элементарных исходов. Чаще всего в качестве элементарных исходов рассматривают множество простейших «неделимых» исходов некоторого опыта. Равновозможность означает намерение приписать исходам одинаковую вероятность. Здесь обычно руководствуются соображениями симметрии.

Элементарные исходы будем обозначать символами .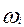

Определение. Пространством элементарных исходов называется множество всех элементарных исходов, которое будем обозначать символом .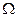

Рассмотрим несколько примеров.

Пример 1. Описать пространство элементарных исходов при подбрасывании монеты.

m Решение. Очевидно, что при подбрасывании монеты возможны два элементарных исхода:

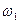 — появление «герба»;

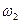 — появление «решки».

Таким образом, пространство элементарных исходов содержит два элемента

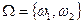. l

Пример 2. Описать пространство элементарных исходов при подбрасывании игрального кубика.

m Решение. Очевидно, что при подбрасывании игрального кубика элементарными исходами является число, выпавших очков, т.е.

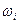 — выпало ровно  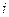очков; .

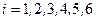Таким образом, пространство элементарных исходов содержит шесть элементов

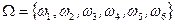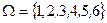 или . l

Пример 3. На отрезке 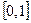 случайным образом отмечается точка. Описать пространство элементарных исходов.

m Решение. В этом случае результатом является координата 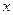, удовлетворяющая условию 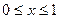. Очевидно, что координата  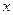меняется непрерывно, пространство элементарных исходов имеет вид

.

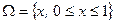Пространство элементарных исходов имеет бесконечно много элементов. l

Определение. Событие называется достоверным, если в результате опыта оно непременно должно произойти.

Достоверное событие обозначают символом 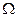, так как оно состоит из тех же элементарных исходов, что и пространство элементарных исходов. Событие, состоящее в появлении менее 7 очков при бросании игрального кубика, является достоверным.

Определение. Событие называется невозможным, если в результате опыта оно не может произойти.

Невозможное событие обозначают символом 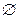. Событие, состоящее в появлении 7 очков при бросании игрального кубика, является невозможным.

Замечание. Каждое случайное событие   можно рассматривать как некоторое подмножество  множества .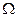

Определение. Элементарные исходы, принадлежащие подмножеству , называются благоприятствующими событию .

 При наступлении каждого элементарного исхода благоприятствующего событию , наступает и само событие , то есть каждый благоприятствующий  исход влечет событие .

Замечание.

Элементарными исходами суммы событий 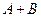 являются элементарные исходы, принадлежащие хотя бы одному из событий  и .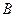

Элементарными исходами произведения событий 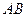 являются те элементарные исходы, которые одновременно принадлежат событиям  и .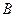

Элементарными исходами разности событий 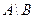 являются те элементарные исходы события , которые не принадлежат событию .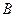

Элементарными исходами противоположного события  являются те элементарные исходы, которые не принадлежат событию .