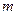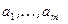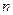Теорема. Из  элементов  и  элементов  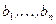можно образовать  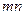пар .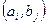

Доказательство. Составим из этих пар прямоугольную таблицу, состоящую из 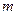 строк и  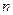столбцов, так, чтобы пара  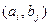стояла на пересечении i-ой строки и j-го столбца. В этом случае каждая пара появляется один и только один раз. Число элементов такой таблицы равно 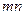. n

Пример 4. Найти число всевозможных исходов при бросании двух игральных костей.

m Решение. Очевидно, что каждый элемент пары принимает шесть значений. Следовательно, существует 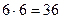 возможных комбинаций. l

Определение. Перестановкой из 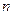 различных элементов называется любой упорядоченный набор этих элементов.

Теорема. Число различных перестановок из 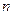 различных элементов вычисляется по формуле:

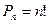. (2.2.1)

Доказательство. Первый элемент можно выбрать 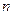 способами, второй элемент можно выбрать  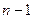способами (т.к. один элемент уже выбран), третий —  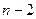способами и т.д. В итоге получим:

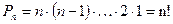. n

Определение. Размещением из 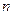 различных элементов по  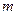называется любой упорядоченный набор из  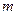элементов, выбранных из общей совокупности в  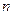элементов.

Теорема. Число различных размещений из 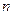 элементов по  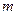вычисляется по формуле:

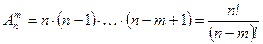. (2.2.2)

Доказательство. Данная теорема доказывается аналогично предыдущей теореме.

Определение. Сочетанием из 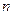 различных элементов по  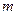называется любой неупорядоченный набор из  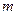элементов, выбранных из общей совокупности в  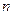элементов.

Теорема. Число сочетаний из 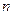 элементов по  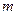вычисляется по формуле:

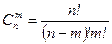. (2.2.3)

Доказательство. Число сочетаний отличается от числа размещений только тем, что входящие в него элементы неупорядочены; 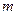 различных элементов можно упорядочить  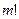способами. Следовательно, каждому размещению соответствует  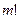сочетаний. Отсюда:

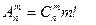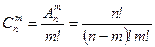 или . n

Способ выбора, приводящий к перестановкам, размещениям и сочетаниям, называется выборкой без возвращения.

Рассмотрим выборку с возвращением. В этом случае каждый взятый элемент из общей совокупности возвращается обратно. Таким образом, один и тот же элемент может быть выбран несколько раз.

Теорема. Число выборок 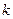 элементов с возвращением из  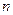различных элементов равно .

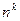Доказательство. Первый элемент может быть выбран 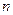 способами, второй также  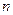способами и т.д. В итоге

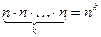. n

Пример 5. (Гипергеометрическое распределение). Предположим, что имеются 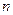 шаров:  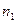красных и  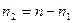черных. Случайным образом выбираются  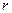шаров. Найти вероятность того, что выбранная группа будет содержать ровно  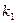красных и  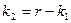черных шаров (событие А).

m Решение. Число способов, которыми можно выбрать, 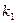 красных шаров из  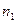шаров ровно 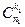. Аналогично, число способов, которыми можно выбрать  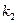черных шаров из  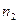равно 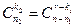. Так как любой выбор красных шаров может комбинировать (составлять пару) с любым выбором черных шаров, имеем число благоприятных исходов, равное .

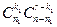Число всевозможных исходов равно .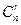

Используя классическое определение вероятности, получаем:

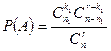. l

Теорема. Пусть 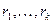 — целые числа, такие, что 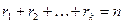. Число способов, которыми множество из  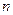элементов можно разделить на  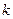упорядоченных подмножеств, из которых первое подмножество содержит  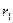элементов, второе – 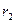элементов и т.д., равно

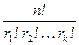. (2.2.4)

Доказательство. Прежде чем доказывать теорему, заметим, что порядок подмножеств существенен в том смысле, что 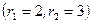 и 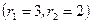 представляет собой разные разбиения; однако, порядок элементов внутри групп игнорируется.

Перейдем к доказательству теоремы. Сначала необходимо выбрать 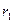 элементов из 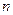; из оставшихся  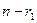необходимо выбрать  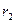элементов и т.д. Получаем:

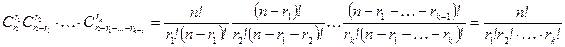.n

Пример 6. Колода карт (52 листа) делится поровну между четырьмя игроками. Найти вероятность того, что каждый игрок имеет туза (событие А).

m Решение. Используя (2.2.4), найдем число всевозможных исходов:

.

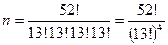Найдем число благоприятных исходов. Четыре туза можно упорядочить 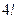 способами, и каждый порядок представляет одну возможность получения одного туза каждым игроком. Оставшиеся 48 карт, согласно (2.2.4), можно распределить  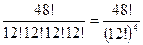способами. Таким образом, число благоприятных исходов равно .

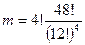Следовательно, искомая вероятность равна

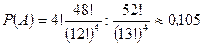. l

Пример 7. Из полной колоды карт (52 листа) вынимаются сразу несколько карт. Какое минимальное число кар нужно вынуть, чтобы с вероятностью, большей чем 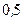, можно было утверждать, что среди них будут карты одной масти.

m Решение. Рассмотрим события 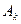 — среди вынутых карт есть хотя бы две карты одной масти. Пусть 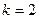. В этом случае число всевозможных исходов равно 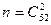. Число благоприятных исходов получаем следующим образом: выбираем масть (4 способа), затем две карты этой масти 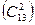, т.е. .

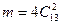Следовательно, используя классическое определение вероятности, получаем:

.

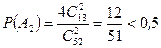Пусть 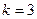. В этом случае число всевозможных исходов равно 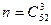. Число благоприятных исходов получаем следующим образом: у нас либо две карты одной масти, либо три карты одной масти, т.е.

.

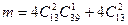Следовательно, используя классическое определение вероятности, получаем:

.

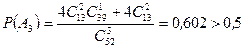Таким образом, необходимо вынуть три карты. l