Из современников Милля, работавших в области логики и неоднократно упоминаемых им в «Системе логики», надо выделить Джона Гершеля и Уильяма Гамильтона.
Джон Гершель (1792 — 11871) — крупнейший английский астроном, работал также в области физики и математики. Для логики имеет значение его труд «Введение в изучение естествознания», опубликованный в 1832 г. В 1868 г. этот труд вышел в русском переводе под заглавием «Философия естествознания».
Для теории индукции Милля трактат Гершеля имеет большое значение. Совершенно правильно говорит В. Минто о методах Милля, основанных на эксперименте: «Главное содержание их Милль заимствовал из практики научных лабораторных исследований, в том виде, в каком их обобщил Гершель. В сущности Милль только констатировал еще раз практические приемы и привел их в систематический вид»1.
По существу для формулировки четырех методов индуктивного исследования Гершель, будучи натуралистом и тем самым — стихийным материалистом, дал нечто более ценное, чем Милль. Милль же, не имевший никакого отношения к естествознанию, сформулировал лишь то, что было выдвинуто Гершелем. При этом Милль перевел всю трактовку вопроса в план субъективного идеализма.
Гершель исходил из опыта. Он писал: «Мы принимаем опыт за великий, единственный и конечный источник нашего
1 В. Минто. Дедуктивная и индуктивная логика. Пер. с англ. М., 1896, стр. 368.
209
знания природы и ее законов. Под опытом мы разумеем опыт не отдельного лица или поколения, но опыт всего человечества, накопившийся во все времена... Опыт можно приобретать двумя способам: во-первых, отмечая факты так, как они случаются, без всякой попытки повлиять на частоту их появления или изменить обстоятельства, при которых они случаются, — это есть наблюдение; во-вторых, приводя в действие причины и орудия, которыми мы располагаем, и изменяя преднамеренно их сочетания с целью заметить происходящие от этого явления; это значит производить эксперименты. На эти два источника мы должны смотреть как на родники всего естествознания» 2.
Наибольшее значение для истории логики имеет VI глава «Введения». Здесь Гершель выдвинул девять правил получения индуктивных выводов. В этой главе за 15 лет до выхода «Логики» Милля дано все, что охватывается известными четырьмя методами индуктивного доказательства.
Со времени Бэкона в истории логики можно считать известными три метода индуктивных доказательств: согласия, разницы и сопутствующих изменений. В дополнение к ним Гершель подчеркнул значение метода остатков.
Формулируя свое девятое правило, в котором содержится определение метода остатков, Гершель писал: «Сложные явления, в, которых различные причины действуют согласно или в противоположных направлениях или, наконец, совершенно независимо одна от другой, но так, что производят сложный результат, могут быть упрощены исключением результата всех известных причин, насколько то позволяет природа случая. Это может быть сделано или путем дедукции или при помощи опыта, и, таким образом, получается остаточное явление, подлежащее объяснению. При помощи этого способа и развивается наука в ее настоящем состоянии. Большая часть явлений, производимых природой, весьма сложна. Если же действия всех известных причин определены с точностью и исключены, то остаточные результаты представляются в виде совершенно новых явлений и сведут к весьма важным заключениям» (§ 158).
Гершель приводит пример из области химии. Так, литий был открыт в связи с тем, что исследователь обратил внимание на избыток веса сернокислой соли, зависевший от того вещества, которое принималось за магнезию в анализируемом минерале. Благодаря тому же принципу удалось выявить, что в незначительных концентрированных остатках от больших операций в технике скрываются неизвестные химические ингредиенты — йод, бром и др.
2 Д. Гершель. Философия естествознания. Пер. с англ. СПб.,. 1868, § 67. Последующие ссылки на это произведение приводятся в тексте и содержат указание на параграф.
210
Естественнонаучная база у Гершеля в положительном смысле отличает его методологический подход по сравнению с Миллем, не владевшим практическими приемами экспериментального исследования. Другое важное преимущество Гершеля, уже чисто теоретическое, заключается в том, что он учитывал взаимодействие факторов. Это есть черта диалектического подхода к изучению действительности — не изолировать, не разобщать явления, а исследовать их в связи.
Согласно Гершелю, одно из предшествующих явлений, фиксируемое по методу сходства как одинаковое во всех случаях, далеко не всегда может быть названо исчерпывающей причиной и в свою очередь может оказаться следствием более первоначального явления, от которого оно зависит.
Свое второе правило, где дана формулировка метода согласия, или сходства, Гершель сформулировал следующим образом: «Всякое обстоятельство, в котором сходны все без исключения факты этой группы, может быть искомой причиной, а если нет, то побочным следствием той же причины. Если окажется только один пункт такого общего сходства, то эта возможность становится достоверностью; с другой же стороны, если таких пунктов будет несколько, то они могут оказаться попутными причинами» (§ 147).
Понятие попутных (или совместно действующих) причин или условий выгодно отличает формулировку Гершеля от формулировки Милля. Последний примитивно истолковывает изолированно взятое сходное условие ряда явлений, абсолютизируя его в качестве исчерпывающей причины.
Тем самым Гершель занимает почетное место среди ученых, исследовавших индукцию. Его нельзя смешивать с поколением всеиндуктивистов. Уже до Милля он исчерпывающе выявил все приемы индуктивного доказательства, ее обнаруживая в то же время недостатка большинства индуктивистов-англичан XIX в. В его взглядах не было субъективно-идеалистических тенденций, свойственных всем позитивистам-индуктивистам вроде Милля или его последователя А. Бэна (1818 — 1903), который также много занимался в области индуктивной логики.
Совсем иного типа по своему философскому складу был другой современник Милля — Уильям Гамильтон (1788 — 1856), которому Милль посвятил целую книгу.
Но, прежде чем излагать логические взгляды Гамильтона, рассмотрим вклад в логику его современника, французского математика и астронома Жергонна (I. D. Gergonne; 1771 — 1859).
Английские логики Гамильтон и в особенности Буль могут быть названы как авторы, которые с помощью объемной интерпретации логических форм заложили основы будущей ал-
211
гебры логики. При этом операция включения является ключом для интерпретации объемных отношений в духе алгебры логики. Чрезвычайно отчетливое выявление форм, связанных с ьключением (или исключением) одного объема из другого, дал Жергонн в своем этюде «Опыт рациональной диалектики» («Essai de dialectique rationelle), напечатанной в «Annales de Mathematiques» (1817, № 7) за 44 года до появления основного труда Буля по алгебре логики.
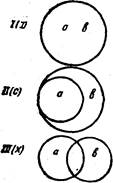
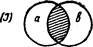
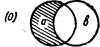
Выдвигая вопрос о понятии включения и соответствующих знаках, Жергонн рассуждает так: чтобы обозначить эти отношения, мы подобрали наиболее подходящие символы для выявления связи между знаком и обозначаемым. Может быть это будет примитивным, но нам представляется это не лишенным значения. Буква Н является начальной для слова «Hors» (вне), она может обозначать систему двух идей, из которых каждая находится за пределами другой, — таковы обе вертикальные линии этой буквы. Обе эти линии можно представить крестообразно, как образующие букву X , которая обозначит систему двух идей, находящихся в отношении перекрещивания. Наконец, эти линии могут быть изображены как совпадающие, и тогда мы получим букву I, чтобы изобразить систему двух равнозначащих идей; эта буква — начальная для слова Identite (равенство). Три эти буквы (Н, X, I) таковы,что они, если их перевернуть, не меняют в силу симметричности своей формы. Иначе обстоит дело с буквой С, когда мы ее переворачиваем (э)- Этой буквой можно обозначить отношение, когда обе идеи начинают играть другую роль при обращении. Буква эта является начальной для двух слов: contenante (содержащее) и contenue (содержимое).
Если обозначить идеи буквами а и в, мы получаем следующие пять схем:
III и IV схемы соответствуют и частноутвердительным, и частноот-рицательным суждениям?
212
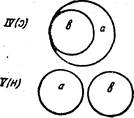
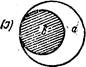
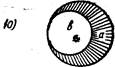
Общеутвердительное (А), общеотрицательное (Е), частно-утвердительное (I) и частноотрицательное (О) суждения сведутся в смысле объемного истолкования к следующему использованию пяти вышеприведенных случаев:
A = I Ú II
E = V
I = III Ú IV
О = Ш Ú IV
Жергонн замечает, что нет такого языка, в котором бы высказывание выражалось со всей точностью и отмежеванностью от других в соответствии с нашими пятью случаями взаимоотношения обоих терминов; такой язык имел бы пять видов высказываний, и диалектика этого языка была бы отличной от того, что дают наши существующие языки.
Бохеньский по поводу приведенного тезиса отмечает, что Жергонн сформулировал мысль, которая имеет значение для логико-математической символики.
После сказанного обратимся к Гамильтону.
Гамильтон был последователем Рида, принадлежавшего к шотландской школе философии здравого смысла. Гамильтон исходил из положений «естественного реализма», которые он формулировал как веру в то, что внешний мир существует, поскольку каждый человек его непосредственно знает, чувствует и воспринимает, как существующий. Тут, конечно, есть верная мысль по сравнению с последователями Юма, которые противопоставляют себя шотландской школе философии здравого смысла. Эти заявления, однако, совмещались у Гамильтона с целым рядом агностических и идеалистических предпосылок, которые сделали из него типичного представителя английской буржуазной философии.
Согласно Гамильтону, в суждении подлежащее подводится под сказуемое или сказуемое является одним из элементов подлежащего. В первом случае мы идем по линии объема, во втором — содержания. Соответственно этому и категорический силлогизм может строиться двояко. Если взаимное отношение
213
терминов в посылках рассматривается с точки зрения объема, то возникает «экстенсивная» форма силлогизма. Если взаимоотношения терминов рассматривается с точки зрения содержания, то получается «интенсивная» форма силлогизма. Терминология Гамильтона получила развитие в современной логике (ср. главу «Метод экстенсионала и интенсионала» в книге Р. Карнапа «Meaning and necessity», 1956.)
Гамильтон говорит: «Если силлогизм развертывается в сторону количества, объема (только эта форма и была обследована логиками), то предикат вывода оказывается наиболее общим целым (greatest whole) и, таким образом, большим термином; субъект вывода составляет наименьший элемент (smallest part) я соответствующим образом оказывается меньшим термином. Если силлогизм развертывается в сторону количества содержания, субъект вывода начинает составлять общее целое и соответствующим образом — больший термин» 3.
Форма экстенсивного силлогизма:
В есть А Все люди смертны
С есть В. Кай — человек
———— ——————
С есть А Кай смертен
Форма интенсивного силлогизма:
С есть В Кай — человек
В есть А Все люди смертны
———— ———————
С есть А Кай смертен
В чистом виде интенсивный силлогизм нельзя обнаружить среди групп классических выводов силлогизма. Последовательность и структура посылок основного интенсивного силлогизма соответствуют модусам четвертой фигуры. Вывод же строится по схеме Barbara (1 фигура). Форма основного интенсивного силлогизма отличается всеми преимуществами естественного хода мысли по сравнению с формами классического силлогизма.
Преимущество толкования суждения с точки зрения содержания и заключается в том, что оно соответствует фактическому развитию познавательной мысли. Когда я утверждаю, что этот поступок справедлив, разве я держу перед своим умственным взором всю сумму справедливых поступков? Не сводится ли здесь ход мысли к тому, что я вскрываю и выявляю одну из характерных черт оцениваемого мною поступка?
3 W. Hamilton. Lectures on logic, ed. 3, vol. I, p. 295.
214
Гамильтон иронизирует по поводу классической четвертой фигуры силлогизма: «Это чудовище, не заслуживающее снисхождения, — вместо того, чтобы держаться одной из двух точек зрения — объема или содержания, эта фигура строит умозаключение, перескакивая от одного к другому»4. Преимущество интенсивного силлогизма в том, что ход мысли в нем соответствует ходу событий, течению и развитию процессов внешнего материального мира.
В самом деле, ведь естественнее рассуждать: «я — человек, а люди смертны, следовательно и я смертен», а не «все люди смертны, я — человек, следовательно я смертен». Отправной пункт рассуждения — я, мой признак — человечность, человечность в свою очередь подразумевает смертность, следовательно смертность приписывается и мне.
Когда говорят «человек — животное», то разумеют, хотя явно этого не выражают, суждение «всякий человек есть животное». Но под животным имеют в виду не всех, а лишь некоторых животных. Из этого явствует, что суждение есть отождествление, приведение в согласие двух понятий в отношении их объема.
Объемно нам дан субъект любого суждения, которым мы оперируем. Предикат же со стороны объема остается неопределенным до тех пор, пока мы не подвергаем его анализу.
Так как обычная классификация суждений учитывает только объем субъекта, то при учете и предиката мы будем иметь четыре вида в пределах только утвердительных суждений, не считая отрицательных.
В утвердительном суждении субъект и предикат могут совпадать по объему. Это будет соответствовать определению «прямая есть кратчайшее расстояние между двумя точками», или «кратчайшее расстояние между двумя точками — это и есть прямая». Но может быть всеобщее суждение иного типа. Например, в суждении «все параллелограммы — четырехугольники» понятие «четырехугольника» шире понятия «.параллелограмм». Затем идут частные суждения, которые могут быть также двух видов в зависимости от объема предиката. Если я говорю: «некоторые змеи имеют ядовитые зубы», то, так как из всех животных только у змеи зубы являются носителями яда, здесь содержится распределенный предикат. А если я скажу «некоторые студенты шахматисты», то объем шахматистов будет шире, чем объем некоторых студентов, которые играют в шахматы, ибо в шахматы играют не одни студенты. По Гамильтону получается не два вида утвердительных суждений, как в традиционной логике, а четыре:
4 W. Hamilton. Lectures on logic, vol. I, pp. 425 — 428.
215
I. toto — totale (обще-общее) — здесь и субъект и предикат взяты в полном объеме;
II. toto-partiale (обще-частное) — субъект взят во всем объеме, предикат взят частично;
III. parti-totale (частно-общее);
IV. parti-partiale (частно-частное).
Таким образом квантифицируется не только субъект, но и предикат. Это учение носит наименование «квантификации предиката».
Можно привести следующие примеры четырех видов утвердительных суждений по Гамильтону: «все равносторонние треугольники суть равноугольные»; «все треугольники суть фигуры»; «некоторые фигуры суть треугольники»; «некоторые треугольники суть нечто равностороннее».
Что представляет собой приведенная классификация? Сам Гамильтон открыто заявляет о выдвинутой им теории тождества, как проводимой в отношении основных типов суждений «с точки зрения их объема». Это говорит автор, который в новой логике со всей отчетливостью противопоставил интенсивную форму суждения экстенсивной. Наметив самостоятельное значение интенсивной формы силлогизма, интенсивного понимания суждения, он сворачивает с этого пути и приходит в конце концов опять к объемной логике. Деление утвердительных суждений на четыре группы учитывает только объем.
Есть у Гамильтона рассуждение, которое имеет очень старомодный характер, что характерно для него как представителя религиозной философии.
Положим, рассуждает Гамильтон, нам дано суждение «бог всемилостив». Согласно теории включения объема, оно будет иметь такой смысл: бог есть одно из всемилостивейших существ, или содержится в числе всемилостивейших существ. Но бог не может быть одним из всемилостивейших существ так как невозможно существование целой группы всемилостивейших существ. Наиболее милостивым может быть только одно существо — именно бог. Естественнее истолковать это суждение так: понятие «бог» содержит в себе понятие «милостивый». Это соответствует непосредственному смыслу высказывания. Иначе говоря, если по объему подлежащее суждения составляет часть сказуемого, то по содержанию, наоборот, сказуемое составляет часть подлежащего5. Смысл суждения в том, что в понятии абсолюта содержится признак «быть всемилостивейшим».
Возьмем более близкий нам пример: суждение «материя протяженна». Искусственным истолкованием этого положения
5 См. W. Hamilton. Lectures on logic, vol. I, p. 274.
216
будет суждение «материя есть одна из различных протяженных вещей». На самом деле естественный ход мысли будет здесь заключаться в том, что в понятии материи выделяется один из признаков, один из существенных ингредиентов.
Игнорируя эту сторону дела, которую он сам же так тонко подметил, Гамильтон строит свою теорию квантификации предиката, т. е. математизирования высказываний. Суждение должно сводиться к уравнению. Гамильтон отличает тождество содержания и тождество объема. Если я утверждаю, что «все люди — смертные существа», то точный смысл этого суждения заключается в том, что все люди — часть смертных, именно та часть, которая состоит из людей. Отсюда тождество объема: сколько людей, столько и смертных существ, называемых людьми. Но можно отождествить эти понятия и по содержанию: если у субъекта (людей) будут признаки a , b , c , d , e , кончая п, то такое же количество признаков будет и у предиката (части смертных существ, называемых людьми). Здесь тождество содержания будет зависеть от тождества объема и по существу совпадать с ним. В результате теория квантификации предиката будет теорией, базирующейся на основе тождества объемов. С этой точки зрения Гамильтона даже формально нельзя причислять к представителям логики содержания.
У Гамильтона есть классификация силлогизмов, в которой он выявляет новые модусы на основе логической формы уравнения. Вместо 14 модусов трех фигур у него получается 108 модусов. Эта система имеет своих сторонников. Так Бенно Эрдман считает, что в основу развития всех побочных форм силлогизма надо положить теорию квантификации Гамильтона. Сочувственный отзыв по адресу классификации Гамильтона мы находим также у неогегельянца Брэдли.
Однако интенсивный вывод в своем специфическом виде стоит у Гамильтона особняком при разработке им форм умозаключений. Если даже ставить себе целью параллельный учет форм объемной логики и логики содержания, считая при этом, что формы первого и второго видов имеют равноправное значение при разработке классификации вывода в целом, то для второго вида Гамильтон не сделал почти ничего, кроме четкого определения его специфики. Свою теорию суждения он построил так, что принцип этого вида выводов оказался им не учтенным, а классификация суждений осуществлена лишь в сфере логики объема.
Мысль Гамильтона о том, что суждение при квантификации сказуемого есть уравнение подлежащего сказуемому, послужила отправным пунктом для учения Джоржа Буля (1815 — 1864) три создании им системы алгебры логики XIX в. с попыткой обобщить задачу дедуктивных умозаключений во-
217
обще. Поэтому Буля следует назвать основоположником современной математической и символической логики. Из ряда его работ по алгебре логики можно в первую очередь назвать «An investigation of the laws of thought» (1854) — «Исследование законов мышления».
Один из его современников, работавший также над проблемами математической логики, де-Морган (о нем речь впереди) рассуждал так: если логика до сих пор не сделала ни одного шага вперед и продолжает пользоваться лишь тем ограниченным запасом символов, который был уже известен Аристотелю, то первая задача логики для ее расширения и упрочения добытых результатов будет в том, чтобы ввести в круг исследования систему искусственных символов, которые бы закрепили необходимые логические понятия в их однозначности с исключением всех лишних психологических оттенков.
С этой целью Буль и вводит логическое исчисление, которое является для «его частью алгебраического исчисления или приложением последнего. Алгебраическое исчисление в логике определяется в системе Буля сведением всех количественных значений к двум: 0 и 1. Он заявляет, что фактически мы можем пренебречь логической интерпретацией символов в логическом уравнении, превратив их в количественные знаки, допускающие лишь значения 0 и 1.
В отношении всей области сущего можно сказать: или в ней нечто есть, или его нет, поэтому то, в чем обязательно нечто есть или не есть, это 1, полнота бытия; Х+Х — 1. С другой стороны, к ничто можно отнести все, что содержит собственное отрицание. Итак, если где имеется собственное отрицание, значит — это 0. Нулевой класс вмещает в себе все, что не существует; X·X = 0.
X и X — это классы, друг друга дополняющие, чтобы образовать универсум. Таким образом, мы получаем возможность логически оперировать классами вещей. Чтобы реализовать подобные операции, надо, по Булю, ввести три группы знаков в логическое исчисление.
1. Сюда относятся прежде всего знаки X , У, Z и т. п. Они обозначают вещи как предметы наших понятий. Таким образом, мы начинаем оперировать всеми мыслимыми понятиями, т. е. классами. Этим символам грамматически соответствуют общие имена и прилагательные.
2. Вторую группу составляют знаки операции; таковыми являются (´), (+), (–) Грамматически эти символы значат (´) — союз «и» (конъюнкция), (+) — «или» (строгая дизъюнкция); (–) — «кроме» или «за исключением».
3. Наконец, главный символ у Буля — это знак тождества (=). Сюда, если учитывать грамматические части речи, отно-
218
сятся все глаголы, но с целью формализации надо их унифицировать, обработав так, чтобы свести к настоящему времени глагола «быть», а содержание переключить в соответствующие понятия. Например, предложение «эти животные жуют жвачку» получает форму: «эти существа = ХУ» (под X разумеются животные, под У — жвачные; вместо знака (´) можно ничего не ставить по принятому в алгебре написанию).
Если X будет значить «мужчина», а У — «женщина», то все люди могут быть обозначены через Х+У («мужчины» + «женщииы»). Буль во главу угла поставил формализацию строгой дизъюнкции; поэтому ослабленную дизъюнкцию, например, «поэты» или «прозаики», не исключающую того, чтобы некоторые поэты являлись и прозаиками, можно символизировать, по Булю, так: X (поэты) + У (прозаики) – (за исключением) ХУ (т. е. тех поэтов, которые одновременно являются прозаиками)
Отличие логики от алгебры логики сводится не только к тому, чтобы количественные знаки имели значение лишь 0 и 1; важное отличие также в том, что для алгебры ХХ=Х2 в логике же XX = X : «синева», уточненная «синевой», останется «синевой». Это правило в свою очередь вытекает из того, что логика есть алгебра, сведенная к значению символов 1 и 0: ведь 1·1=1, так же как 0·0=0. Таким образом, значение того, что современная математическая логика разумеет под идемпотентностью, было установлено системой Буля. Что касается тождества нулю, то такие формулы Буль просто откидывает — он не признавал пустых множеств, т. е. классов, равных 0, и не умел ими оперировать.
С помощью знака (– ) мы, по Булю, образуем отрицательные классы. «Все люди ( X ), кроме европейцев (У)» мы формализуем так: X – У. «Не люди» формализуются следующим образом: 1 (универсум) минус X : итак, 1 – X будет значить «не люди». Если под X будем разуметь «светила», под У — «солнца» (центральные небесные тела всех систем, в том числе и нашей солнечной системы), под Z — планеты, то мы можем получить X = У + Z (светила — это солнца или планеты); X – Z = У (светила, кроме планет, — это солнца); Z = X — У (планеты — это все светила, кроме солнца).
Буль своей системой достигает возможности расширения обычной силлогистики. Для алгебры логики Буля силлогизм — простейший Случай некоторой общей задачи выведения всего, что можно извлечь из суждения по отношению к тому или иному классу. В этом суть опосредствованных умозаключений путем элиминации, с помощью которой мы исключаем из уравнений те или иные логические термины, подобно тому как исключают средний термин из посылок силлогизма.
219
В самом деле, мы можем составить уравнение: «кандидаты наук — это лица, защитившие кандидатскую диссертацию»; X = У, в таком случае X – У = 0; кандидатов наук, которые не оказались бы лицами, защитившими кандидатскую диссертацию, нет.
Но может быть и такое уравнение: «окончившие аспирантуру, — это те, кто сдал кандидатский минимум и представил готовую диссертацию», X = У Z ; в таком случае мы будем иметь X – У Z = 0. Тут мы элиминируем два множества.
В первом случае мы имеем функцию от X и У (от двух терминов), во втором случае- — от трех ( X , У, Z ). Простой случай — обычный силлогизм: исключение одного термина из системы трех терминов. Буль идет дальше: согласно его толкованию, проблема исключения средних терминов ставит себе гораздо более широкие цели. Она имеет в виду не только исключение одного термина из двух предложений, но вообще исключение средних терминов из предложений, каково бы ни было число тех и других я каковы бы ни были их связи.
Таким образом, Буль достигает больших обобщений при решении задач выводной деятельности ума по сравнению с традиционной логикой.
Узость алгебры логики Буля в том, что он все сводит к эквивалентности: Х – У или Х ≠ У и т. д. Формулы Х ≤ У или У ≤ X он не употреблял и в свою логическую систему не вводил. Такими формулами стали пользоваться уже продолжатели его дела.
Рядом с Гамильтоном следует поставить логика Стенли Джевонса (1835 — 1882), подвизавшегося также в качестве экономиста. Как логик он примыкал к Булю. Джевонс считал, что хотя сложные математические формулы Буля и не имеют особого значения, но он (Джевонс) использует элементарные методы исчисления. Джевонс является изобретателем первой логической машины. Его перу принадлежат «Элементарный учебник логики» (1870) и «Основы науки» (1874). Обе эти книги переведены на русский язык философом и революционным демократом М. А. Антоновичем. Джевонс отвергает теорию квантификации сказуемого Гамильтона и выдвигает свою теорию спецификации сказуемого. Он считает, что слово «некоторые», которым пользуется Гамильтон, слишком неопределенно. Оно указывает лишь на то, что какая-то часть объема сказуемого в суждении совпадает с объемом подлежащего, причем остается совершенно неясным, какая точно часть имеется в виду. Между тем легко найти нужный прием. Если ивантифицировать сказуемое, то мы будем иметь, например, предложение «все млекопитающие суть некоторые позвоночные». В отношении понятия «некото-
220
рые» следует добиться уточнения, и тогда мы определим его так: «те самые позвоночные, которые вместе с тем являются млекопитающими». Под сказуемым будут тем самым иметься в виду млекопитающие позвоночные. Итак, суждение «млекопитающие — позвоночные», выраженное в символе «А суть В», будет выявлено следующим образом: «А суть АВ», т. е. «все млекопитающие суть млекопитающие позвоночные».
В дедукции необходимо иметь одно суждение равенства, ибо, по учению Джевонса, неравенство никак не может служить подливным основанием для умозаключения. Если мы знаем, что собор Павла в Лондоне и Вестминстерское аббатство порознь не равны по высоте собору Петра в Риме, то заключения получить нельзя; необходимо тождество в направлении двух различий.
Таким образом, общее и единственное правило дедукции будет опираться на возможность замещения одного термина другим, поскольку мы будем иметь посылку о том, что один термин тождествен другому. Поэтому, если будет иметься посылка о полном тождестве, например «высочайшая гора в Европе — Монблан», и другая, например «Монблан покрыт снегом» (в истолковании Джевонса это будет «Монблан-Монблан, покрытый снегом», А = АВ), то путем замещения мы получаем вывод: «высочайшая гора в Европе покрыта снегом». Это будет суждение тождества:
А = В
В = ВС
———
А = ВС
Теорией замещения Джевонса воспользовался русский логик М. И. Каринский, построив на принципе тождества свою «классификацию выводов».
К середине прошлого века следует отнести появление новой теории в логике — логики отношений. Пионером в этом направлении выступил английский логик де-Морган (1806 — 1878). Морган сосредоточил свое внимание на природе связки в суждении. В своем сочинении «Формальная логика» (1847) он обращает внимание на то, что связка есть отношение. Морган не согласен с тем, что связка представляет собой нечто единообразное. Если связка есть отношение, то она может оказаться носителем любого отношения, а их — необозримое множество. Связка, как отношение, может обозначать тождество, равенство, включение; употребляться в смысле «быть больше», «быть меньше», «быть братом» и т. д. Исчерпывающе анализировать все виды связок, которые являются отношениями, невозможно, — в таком случае составилась бы
221
целая энциклопедия, «да еще с ежегодными добавлениями»6. Свести значение всех отношений к одному смыслу связки было бы насилием над логикой и ни к чему бы не привело. Нужно выявить общие условия связок (copular conditions). Таких условий Морган находит несколько.
Первое условие — обратимость или симметричность: ARB → BRA . Если непосредственно связка необратима, то следует найти соответствующую соотносительную связку, например: «если А есть отец В, то В — сын А».
Второе условие — переходность, или транзитивность. Свойство переходности состоит в том, что, если какой-нибудь предмет находится порознь в известном отношении к двум другим предметам, то и эти последние находятся в том же отношении между собою7.
Формальная логика, согласно Моргану, имеет дело не с предметами и не с понятиями, а с именами. Отсюда Морган определяет силлогизм как умозаключение об отношении между двумя именами на основании отношения каждого из этих имен порознь к какому-либо третьему8
Отдельные связки в суждениях, по мнению Моргана, имеют материальный характер, ибо они отличаются друг от друга особенностями, присущими материалу: то отношение означает тождество, то — причинную зависимость, то — быть сыном или дочерью, быть выше, быть ниже, быть больше, быть меньше и т. д.
Но считая, что логика должна быть формальной логикой, Морган стремится оставить в стороне все эти «материальные» особенности и рассматривать связку как отношение вообще. Он начинает подыскивать символы, обозначает общее отношение буквой L и т. п. Так было положено начало символической, логики в собственном смысле слова (отдельные символические обозначения вроде А, Е, J , О были приняты и в традиционной логике).
Многие правила, выдвинутые Морганом, так прочно вошли в состав математической логики, что называются правилами Моргана. Таковы две основные закономерности, устанавливающие связь между дизъюнкцией и конъюнкцией.
1) Отрицание конъюнкции двух членов (высказываний) равнозначно дизъюнкции этих членов, взятых с отрицательным знаком:
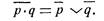
6 de-Morgan. Formal logic or the calculus of inferense necessary and probable. L., 1847, pp. 49 — 50.
7 Ibid., p. 57.
8 Ibid., p. 76.
222
2) Отрицание дизъюнкции двух членов (высказываний) равнозначно конъюнкций этих членов, взятых каждый в отдельности с отрицательным знаком:
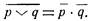
Морган впервые ввел утвердившееся в математической логике выражение «универсум рассуждения» (universe of discourse)
К Моргану примыкал Герберт Спенсер (1820 — 1903). Оригинальность его позиции заключается в том, что с его точки зрения логика должна заниматься не именами и мыслями, а самими вещами.
Для Спенсера предмет логики — наиболее общие законы отношений между разными вещами; отсюда его понимание логики как объективной науки. Поэтому, согласно Спенсеру, логика противоположна теории познания, которая анализирует общие законы отношений между представлениями, соответствующими объективным вещам. Спенсер твердо убежден в существовании таких внепсихических вещей.
Рядом с определенным сознанием, законы которого формулирует логика, существует неопределенное сознание, не поддающееся никаким формулировкам. Мышление сводится лишь к установлению отношений между представлениями. Для Спенсера, разделявшего биологическую точку зрения, только такое мышление является полезным.
Логика, по Спенсеру, имеет дело не с фактами сознания, не с представлениями и понятиями, не с отражением вещей в мышлении, а с самими вещами. Такую точку зрения можно было бы назвать вульгарным материализмом в логике.
Исходным пунктом логических рассуждений Спенсера, который мы находим в его «Психологии» (переведена на русский язык в 1898 г.), является утверждение о том, что логика есть наука не о словах и не о мыслях, а наука о формах, в которых нам даны явления.
За основной тип суждений Спенсер берет определенный вид частных суждений, вскрытых Морганом. Если имеется понятие большинства: «большинство В суть С» и «большинство В суть А», то из таких двух частных посылок можно сделать вывод: «некоторые А суть С»
Приведем рассуждение самого Спенсера: «Чтобы показать, что утверждения логики относятся к связям между предметами, рассматриваемыми как существующие отдельно от нашего сознания, а не к соотносительным связям между нашими соотносительными состояниями сознания, достаточно будет рассмотреть какой-либо числовой пример логического предложения из системы проф. Моргана. На основании посылок «боль-
223
шинство В суть С» и «большинство В суть А» — можно с уверенностью заключить, что «некоторые А суть С», — ведь два отдела класса В, захватывающие каждый более половины всего класса, должны необходимым образом состоять отчасти из тех же самых индивидов. Так, если 60% В суть С и 70% В суть А, то по крайней мере 30% будут общими для А и С. Если мы возьмем силлогизм, который будет представлять не одну только числовую определенность, но в котором на месте символических терминов будут поставлены термины, выражающие реальность, то объективный характер рассматриваемых нами отношений выступит с еще большей ясностью» 9.
Спенсер приводит следующий пример: класс В — число животных на ферме. Он состоит из двух частей — часть коров и часть овец. Класс С — овцы, 60%. Класс А — больные животные, 70%. Вывод: «во всяком случае некоторые больные животные суть овцы». Таких будет 30%. Здесь имеются в виду необходимые объективные отношения. Это силлогизм, в котором фигурируют не мысли об овцах, а сами овцы и стадо.
Английский логик Карвет Рид в 1878 г. выпустил книгу «О теории логики» («On the theory of logic. An essay»), в предисловии которой указывал на то, что в основу его опыта построения логики положено спенсеровское понимание логики как науки об отношениях самих вещей.
Точка зрения Спенсера является ошибочной, так как он смешивает законы природы с законами логики. Законы логики являются лишь отражением наиболее общих отношений между вещами, т. е. законов самой действительности. Логика вовсе не отличается три конкретностью, которую мы находим в любой науке, устанавливающей закономерности природы. Логика есть наука абстрактная, и в этом отношении она действительно выделяет наиболее простые отношения между мыслями, но такие, которые являются лишь отражением объективной закономерности.
Правильно замечает Циген, автор «Lehrbuch der Logik» (1920), что этот взгляд нужен был Карвету Риду только для того, чтобы написать такое широковещательное предисловие. Фактически же, когда он переходит к изучению отдельных форм мышления, отдельных фигур, он об этом забывает и трактует их иначе.
Особую роль в развитии алгебры логики сыграла Xристина Лэдд Франклин (1847 — 1930), американский психолог и логик. Еще в логике Аристотеля содержалось учение о связи трех фигур силлогизма, которое развил Лейбниц своим указанием на возможность выведения модусов второй и треть-
9 Н. Spencer, The principles of psychology, vol. II, 1872, pp. 88 — 89
224
ей фигур из первой средствами закона противоречия. В «Новых опытах» он пишет: «Для этого надо предположить, что модусы первой фигуры правильны и что, следовательно, если признать заключение ложным (или противоречащее ему суждение истинным) и принять за истинную также одну из посылок, то суждение, противоречащее другой посылке, будет истинным» (стр. 320). Это учение в конце XIX в. получило название антилогизма. Оно было выдвинуто Христиной Франклин первоначально в виде следующего лаконичного предписания: «Возьми предложение, противоречащее выводу, и смотри, чтобы общие суждения были выражены отрицательно, а частное положительно. Если два предложения — общие, третье — частное, и если термин, одинаковый у двух общих предложений, имеет в них различный знак, то в этом и только в этом случае силлогизм состоятелен» 10.
По принципу антилогизма модусы трех первых фигур распадаются на четыре триады:
Barbara, Baroco, Bocardo
Celarent, Festino, Disarms
Darii, Camestres, Ferison
Ferio, Cesare, Datisi.
Система силлогизмов в алгебре логики исключительно проста. Соответствующие три правила служат одновременно приемом, заменяющим аксиому силлогизма, средством, определяющим различие фигур и модусов, а также критерием, в соответствии с которым легко отсеять все ложные силлогизмы. Правила эти при определении триад антилогизмов получили в современной логике следующую формулировку:
1) должно быть два общих суждения (= 0) и одно частное ( ≠ 0);
2) два общих суждения должны иметь один совпадающий термин, который один раз должен быть положительным, а другой раз — отрицательным;
3) частное суждение соединяет через неравенство ( ≠ 0) остальные два термина, которыми различаются два общие суждения11.
10 «Studies in logic», ed. by Ch. Peirce, 1883, p. 41.
11 См. R. Eaton. General logic, 1931, p. 137.
Глава XV . ЛОГИКА XIX в.
Дата: 2019-02-25, просмотров: 372.