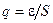Карта стандартных отклонений
⇐ ПредыдущаяСтр 29 из 29
Поможем в ✍️ написании учебной работы
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

 

Изменение показателя технологического рассеивания процесса — стандартного отклонения σ может быть проанализировано с использованием контрольных карт размахов (обычно при построении карт вручную), стандартных отклонений или карт дисперсий.

Проверяется нулевая гипотеза Н0: σ2 = σ02 при альтернативе Н1,: σ2 ≠ σ02. На карте стандартных отклонений откладываются значения st, вычисляемые по формуле (4). При определении положения контрольных границ предполагается, что случайная величина S имеет приблизительно нормальное распределение со средним значением, равным 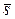, и со стандартным отклонением, равным .

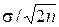Для правила «трех сигм» контрольные границы S-карты можно найти, используя коэффициенты, приведенные в таблице 1: при известном σ нижняя контрольная граница равна LCL = B1σ, верхняя UCL = В2σ; при неизвестном значении σ соответственно 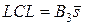 и 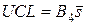. При n < 6 нижние контрольные границы этих карт нулевые: LCL = 0 (чтобы исключить физически невозможные отрицательные значения, получающиеся по соответствующим зависимостям).

Возможны и другие способы построения контрольных карт стандартных отклонений [3].

 

Пример 1. Контролируется содержание хрома в стальных отливках. В каждую смену проводятся замеры в четырех плавках. В контрольном листке (рис. 4.2) приведены данные по 15 подгруппам (сменам). Требуется построить 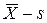-карты Шухарта.

 

Цех

Деталь

Характеристика

Объем выборок

Дата

Операция

Рабочий

Предельные значения

Частота выборок

Расчеты выполнил
№

x 1

x 2

 x 3

x 4

s
1

0,74

0,76

 0,62

0,73

0,713

 0,0629
2

0,72

0,74

 0,84

0,69

0,748

 0,0650
3

0,87

0,79

 0,70

0,92

0,820

 0,0963
4

0,78

0,66

 0,71

0,74

0,723

 0,0506
5

0,81

0,66

 0,82

0,67

0,740

 0,0868
6

0,63

0,71

 0,68

0,82

0,710

 0,0804
7

0,63

0,73

 0,64

0,80

0,700

 0,0804
8

0,66

0,68

 0,85

0,91

0,775

 0,1240
9

0,63

0,66

 0,62

0,85

0,690

 0,1080
10

0,85

0,61

 0,75

0,77

0,745

 0,0998
11

0,73

0,65

 0,74

0,90

0,755

 0,1047
12

0,85

0,77

 0,65

0,69

0,740

 0,0887
13

0,67

0,69

 0,83

0,62

0,703

 0,0900
14

0,74

0,73

 0,62

0,88

0,743

 0,1066
15

0,81

0,82

 0,69

0,73

0,763

 0,0629
                     

Рис. 4. Контрольный листок с данными о содержании хрома в стальных отливках

В последних двух столбцах контрольного листка приведены рассчитанные средние значения и стандартные отклонения в каждой подгруппе, найденные по формулам (1) и (4) соответственно. Например, для первой подгруппы имеем:

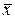= 0,74 + 0,76 + 0,62 + 0,73;

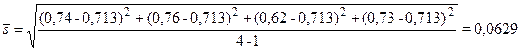
Оценка среднего уровня процесса по формуле (3):

,

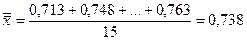а среднее стандартное отклонение по формуле (5):

.

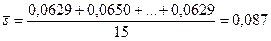Положение контрольных границ карты средних значений найдем по формуле (12), в которой коэффициент А3 по таблице 1 при n = 4 равен А3 = 1,628:

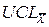 = 0,738 + 1,628·0,087 = 0,880;

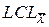 = 0,738-1,628·0,087 = 0,596.

Для расчета положения контрольных границ карты стандартных отклонений учтем, что для нее LCLs = В3 s и UCLs = В4 s , при этом при n < 6 (у нас n = 4) нижняя контрольная граница этой карты нулевая: LCL$ = 0. По таблице 1 при п = 4 В4 = 2,266, тогда

UCLS= 2,266 0,087 = 0,197.

 

Откладывая на карте средних значения предпоследнего столбца контрольного листка по рис. 4, а на карте стандартных отклонений — последнего столбца, построим соответствующие карты Шухарта (рис. 5). Видим, что ни одна из построенных карт не указывает на наличие нарушений процесса (ни на карте средних, ни на карте стандартных отклонений нет точек, выходящих за контрольные границы): процесс статистически управляем.

 

 

 


Карта размахов

 

Для построения карты размахов (R-карты) значения размахов мгновенной выборки вычисляются по формуле (8). На практике при использовании правила «трех сигм» положение контрольных границ определяется с помощью данных таблицы 1: при известном σ нижняя контрольная граница равна LCL = D1σ, верхняя UCL = D2σ; при неизвестном значении σ соответственно 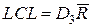 и 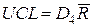. При n < 7 нижние контрольные границы этих карт нулевые.

Карта медиан

Эта карта используется как альтернатива карте средних значений: она требует меньшего числа вычислений. Следует иметь в виду, что эта карта менее чувствительна к нарушениям процесса, поэтому при использовании компьютерной техники для анализа среднего уровня настройки процесса целесообразно строить карту средних значений.

В то же время при несимметричном распределении показателя качества часто медиана оказывается более объективной характеристикой среднего уровня процесса.

Медиана в подгруппе (мгновенной выборке) Met при нечетном объеме подгруппы определяется как центральное значение вариационного ряда (упорядоченного по возрастанию данных в подгруппе). При четном числе наблюдений в качестве медианы используется среднее арифметическое из двух центральных значений вариационного ряда.

Рассеяние процесса оценивается по среднему размаху .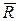

Среднее значение медианы при m мгновенных выборках

.                                              (13)

Границы регулирования карты медиан

 

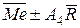,                                                         (14)

где коэффициент A4 определяется по таблице 1.

 

Пример 2. Контролируется средний вес упаковки продукта на автоматической линии. Каждый час взвешиваются по три упаковки; в контрольном листке приведены данные за 20 часов (рис. 6).

Принято решение об использовании контрольной карты медиан. В контрольном листке, кроме исходных данных, приведены значения медиан Me в каждой подгруппе (вариационный ряд включает по три наблюдения, медианой является второе из них) и размахов R.

 

Среднее значение медианы

 

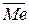 = (505 + 508 + ... + 503) / 20 = 504,45,

 

а средний размах

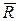 = (14+11+...+7)/20= 7,45.

 

Тогда контрольные границы карты медиан, в соответствии с формулой (14), учитывая, что при n = 3 коэффициент A4 по таблице 1 равен 1,19:

 

UCLMe = 504,45 + 1,19 -7,45 = 513,31;

LCLMe = 504,45 - 1,19 • 7,45 = 495,58.

 

 

Цех

Деталь

Характеристика

Объем выборок

Дата

Операция

Рабочий

Предельные значения

Частота выборок

Расчеты выполнил
№

x 1

x 2

x 3

Me

R 1

510

505

496

505

14 2

508

512

501

508

11 3

499

501

504

501

5 4

506

504

500

504

6 5

508

507

499

507

9 6

500

504

502

504

4 7

501

496

511

501

15 8

502

504

509

504

7 9

507

510

501

507

9 10

502

504

500

502

4 11

501

506

498

501

8 12

496

499

503

499

7 13

513

508

509

509

5 14

510

506

507

507

4 5

504

505

508

505

4 16

506

507

512

507

6 17

513

510

508

510

5 18

504

506

498

504

6 19

496

501

509

501

13 20

501

503

508

503

7                    

 

Рис. 6. Контрольный листок с данными о весе упаковок продукта

 

 

На рис. 7 показана контрольная карта медиан. Как правило, для управления процессом при использовании карты медиан используется одновременно и карта размахов (для контроля рассеяния процесса).

 

Таблица 1. Коэффициенты для построения контрольных карт

 

n c d A 1 A 2 A 3 A 4 B 1 B 2 B 3 B 4 D 1 D 2 D 3 D 4
2 0,798 1,128 2,121 1,880 2,659 1,88 0 2,606 0 3,267 0 3,686 0 3,267
3 0,889 1,693 1,732 1,023 1,954 1,19 0 2,276 0 2,568 0 4,358 0 2,574
4 0,921 2,059 1,500 0,729 1,628 0,80 0 2,088 0 2,266 0 4,696 0 2,282
5 0,940 2,326 1,342 0,577 1,427 0,69 0 1,964 0 2,089 0 4,918 0 2,114
6 0,952 2,534 1,225 0,783 1,287 0,55 0,029 1,874 0,030 ,970 0 5,078 0 2,004

 

 

Контрольные вопросы и задачи для приобретения знаний по теме 8

 

1. Приведите последовательность процедур статистического анализа точности процесса методом малых выборок.

2. Приведите возможные причины неоднородности дисперсий двух смежных выборок. Установлено неравенство средних двух смежных выборок. О чем это свидетельствует и какие возможные причины могут вызвать эту ситуацию?

3. Поясните сущность метода точечных диаграмм оценки стабильности процесса обработки деталей.

4. Перечислите двойные карты Шухарта, которые строят при статистическом управлении процессом обработки деталей?

5. Когда по данным контрольных карт Шухарта считают, что процесс обработки деталей не является статистически управляемым?

Литература

 

1. Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В.Е. Гмурман. М.: Высш. шк., 2004. -479 с.

2. Солонин И. С. Математическая статистика в технологии машиностроения / И. С. Солонин. М.: «Машиностроение», 1972. – 216 с.

3. Горелова Г.В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. Учебное пособие для вузов / Г.В. Горелова, И.А. Кацко. Ростов н/Д: Феникс, 2005, -480 с.

4. Кацев П. Г. Статистические методы исследования режущего инструмента / П. Г. Кацев. М.: Машиностроение, 1974. 231 с.

5. Вентцель Е. С. Теория вероятностей: Учебник для студ. вузов /Е. С. Вентцель. - М.: Издательский центр «Академия», 2005. - 576 с.

6. Анализ точности и стабильности процессов: учеб. пособие / Ю.М. Быков, А.Г. Схиртладзе, С.Ю. Быков, С.А. Схиртладзе. – Старый Оскол: ТНТ, 2011. 96 с.

7. Клячкин В. Н. Статистические методы в управлении качеством: компьютерные технологии: Учеб. пособие / В. Н. Клячкин. - М.: Финансы и статистика; ИНФРА-М, 2009. -304 с.

Приложение

Таблица П1. Значение функции Лапласа

t 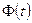t 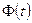t 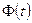t 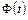t 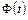t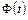
0,00 0,000 0,48 0,1845 0,96 0,3315 1,44 0,4250 1,92 0,4725 2,40 0,4920
0,01 0,004 0,49 0,1880 0,97 0,3340 1,45 0,4265 1,93 0,4730 2,41 0,4920
0,02 0,008 0,50 0,1915 0,98 0,3365 1,46 0,4280 1,94 0,4740 2,42 0,4920
0,03 0,012 0,51 0,1950 0,99 0,3390 1,47 0,4290 1,95 0,4745 2,43 0,4925
0,04 0,016 0,52 0,1985 1,00 0,3415 1,48 0,4305 1,96 0,4750 2,44 0,4925
0,05 0,020 0,53 0,2020 1,01 0,3440 1,49 0,4320 1,97 0,4755 2,45 0,4930
0,06 0,024 0,54 0,2055 1,02 0,3460 1,50 0,4330 1,98 0,4760 2,46 0,4930
0,07 0,028 0,55 0,2090 1,03 0,3485 1,51 0,4335 1,99 0,4765 2,47 0,4930
0,08 0,032 0,56 0,2125 1,04 0,3510 1,52 0,4355 2,00 0,4775 2,48 0,4935
0,09 0,036 0,57 0,2155 1,05 0,3530 1,53 0,4370 2,01 0,4780 2,49 0,4935
0,10 0,040 0,58 0,2190 1,06 0,3555 1,54 0,4390 2,02 0,4785 2,50 0,4940
0,11 0,044 0,59 0,2225 1,07 0,3575 1,55 0,4395 2,03 0,4790 2,51 0,4940
0,12 0,048 0,60 0,2255 1,08 0,3600 1,56 0,4405 2,04 0,4795 2,52 0,4940
0,13 0,0515 0,61 0,2290 1,09 0,3620 1,57 0,4420 2,05 0,4800 2,53 0,4945
0,14 0,0555 0,62 0,2325 1,10 0,3645 1,58 0,4430 2,06 0,4805 2,54 0,4945
0,15 0,0595 0,63 0,2355 1,11 0,3665 1,59 0,4440 2,07 0,4810 2,55 0,4945
0,16 0,0635 0,64 0,2390 1,12 0,3685 1,60 0,4450 2,08 0,4810 2,56 0,4950
0,17 0,0675 0,65 0,2420 1,13 0,3710 1,61 0,4465 2,09 0,4815 2,57 0,4950
0,18 0,0715 0,66 0,2455 1,14 0,3730 1,62 0,4475 2,10 0,4820 2,58 0,4950
0,19 0,0755 0,67 0,2485 1,15 0,3740 1,63 0,4485 2,11 0,4825 2,59 0,4950
0,20 0,0795 0,68 0,2520 1,16 0,3770 1,64 0,4495 2,12 0,4830 2,60 0,4955
0,21 0,0830 0,69 0,2550 1,17 0,3790 1,65 0,4505 2,13 0,4835 2,61 0,4955
0,22 0,0870 0,70 0,2580 1,18 0,3810 1,66 0,4515 2,14 0,4840 2,62 0,4955
0,23 0,0910 0,71 0,2610 1,19 0,3830 1,67 0,4526 2,15 0,4840 2,63 0,4955
0,24 0,0950 0,72 0,2640 1,20 0,3850 1,68 0,4535 2,16 0,4845 2,64 0,4960
0,25 0,0985 0,73 0,2675 1,21 0,3870 1,69 0,4545 2,17 0,4850 2,65 0,4960
0,26 0,1025 0,74 0,2705 1,22 0,3890 1,70 0,4555 2,18 0,4855 2,66 0,4960
0,27 0,1065 0,75 0,2735 1,23 0,3905 1,71 0,4565 2,19 0,4855 2,67 0,4960
0,28 0,1105 0,76 0,2765 1,24 0,3925 1,72 0,4575 2,20 0,4860 2,68 0,4965
0,29 0,1140 0,77 0,2795 1,25 0,3945 1,73 0,4580 2,21 0,4865 2,69 0,4965
0,30 0,1180 0,78 0,2825 1,26 0,3960 1,74 0,4590 2,22 0,4870 2,70 0,4965
0,31 0,1215 0,79 0,2850 1,27 0,3980 1,75 0,4600 2,23 0,4870 2,71 0,4965
0,32 0,1255 0,80 0,2880 1,28 0,4000 1,76 0,4610 2,24 0,4875 2,72 0,4965
0,33 0,1295 0,81 0,2910 1,29 0,4015 1,77 0,4615 2,25 0,4880 2,73 0,4965
0,34 0,1330 0,82 0,2940 1,30 0,4030 1,88 0,4625 2,26 0,4880 2,74 0,4970
0,35 0,1370 0,83 0,2965 1,31 0,4050 1,89 0,4635 2,27 0,4885 2,75 0,4970
0,36 0,1405 0,84 0,2995 1,32 0,4065 1,80 0,4640 2,28 0,4885 2,76 0,4970
0,37 0,1445 0,85 0,3025 1,33 0,4080 1,81 0,4650 2,29 0,4890 2,77 0,4970
0,38 0,1480 0,86 0,3050 1,34 0,4100 1,82 0,4655 2,30 0,4895 2,78 0,4975
0,39 0,1515 0,87 0,3080 1,35 0,4115 1,83 0,4665 2,31 0,4895 2,79 0,4975
0,40 0,1555 0,88 0,3105 1,36 0,4130 1,84 0,4670 2,32 0,4900 2,80 0,4975
0,41 0,1590 0,89 0,3135 1,37 0,4145 1,85 0,4680 2,33 0,4900 2,81 0,4975
0,42 0,1630 0,90 0,3160 1,38 0,4160 1,86 0,4685 2,34 0,4905 2,82 0,4975
0,43 0,1665 0,91 0,3180 1,39 0,4175 1,87 0,4695 2,35 0,4905 2,83 0,4975
0,44 0,1700 0,92 0,3210 1,40 0,4190 1,88 0,4700 2,36 0,4910 2,84 0,4975
0,45 0,1735 0,93 0,3240 1,41 0,4205 1,89 0,4705 2,37 0,4910 2,85 0,4975
0,46 0,1770 0,94 0,3265 1,42 0,4220 1,90 0,4715 2,38 0,4915 2,86 0,4980
0,47 0,1810 0,95 0,3290 1,43 0,4235 1,91 0,4720 2,39 0,4915 2,87 0,4980

Таблица П2. Значения 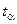, для которых вероятность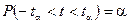

k

вероятность a
0,9 0,95 0,98 0,99 0,999
1 6,31 12,71 31,82 63,66 636,2
2 2,02 4,30 6,97 9,93 31,60
3 2,35 3,18 4,54 5,84 12,94
4 2,13 2,78 3,75 4,60 8,61
5 2,02 2,57 3,37 4,03 6,86
6 1,94 2,45 3,14 3,70 5,96
7 1,90 2,37 3,00 3,50 5,40
8 1,86 2,30 2,90 3,36 5,04
9 1,83 2,26 2,82 3,25 4,78
10 1,81 2,23 2,76 3,17 4,59
11 1,80 2,20 2,72 3,11 4,49
12 1,78 2,18 2,68 3,06 4,32
13 1,77 2,16 2,65 3,01 4,22
14 1,76 2,14 2,62 2,98 4,14
15 1,75 2,13 2,60 2,95 4,07
16 1,75 2,12 2,58 3,92 4,02
17 1,74 2,11 2,57 2,90 3,97
18 1,73 2,10 2,55 2,88 3,92
19 1,73 2,09 2,54 2,86 3,88
20 1,72 2,09 2,53 2,85 3,85
21 1,72 2,08 2,52 2,83 3,82
22 1,72 2,07 2,51 2,82 3,79
23 1,71 2,07 2,50 2,81 3,77
24 1,71 2,06 2,49 2,80 3,75
25 1,71 2,06 2,49 2,79 3,72
26 1,71 2,06 2,48 2,78 3,71
27 1,70 2,05 2,47 2,77 3,69
28 1,70 2,05 2,47 2,76 3,67
29 1,70 2,05 2,46 2,76 3,66
30 1,70 2,04 2,46 2,45 3,65
40 1,68 2,02 2,42 2,70 3,55
60 1,67 2,00 2,39 2,66 6,46
120 1,66 1,98 2,36 2,62 3,37
  1,65 1,96 2,33 2,58 3,29

 

Таблица П3. Значения вероятностей ;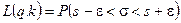

 

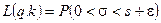
k

0,10 0,15 0,20 0,25 0,30 0,40 0,50 0.60 0,70 0,80 0,90 1,00 1,25
6 0,264 0 388 0,501 0,599 0,681 0,791 0,849 0,886 0,913 0,933 0,948 0,959 0,978
8 305 444 567 669 748 845 895 926 948 963 974 981 991
10 340 491 620 722 797 882 925 961 968 979 986 991 997
12 371 532 664 764 833 900 946 968 980 988 993 996 999
14 399 567 701 798 862 929 960 978 988 993 996 998 999
16 425 599 733 826 885 944 971 985 992 996 998 999 1,000
18 448 627 760 849 903 955 980 990 996 998 999 999 —
20 470 652 784 868 918 964 984 993 997 999 999 1,000 —
25 518 706 832 905 944 979 992 997 999 1,000 1,000 — —
30 559 749 867 930 962 988 996 999 1,000 — — — —
35 597 787 893 944 969 990 997 999 — — — — —
40 628 815 913 957 978 994 999 1,000 — — — — —
45 657 840 929 967 984 996 999 — — — — — —
50 682 860 942 974 993 998 999 — — — — — —
60 726 893 960 984 996 999 1,000 — — — — — —
70 762 917 972 990 998 1,000 — — — — — — —
80 792 935 980 994 999 — — — — — — — —
90 818 949 986 996 999 — — — — — — — —
100 840 959 990 997 1,000 — — — — — — — —
150 914 986 998 1,000 — — — — — — — — —
200 951 995 1,000 — — — — — — — — — —
250 972 998 1,000 — — — — — — — — — —
500 998 1,000 1,000 — — — — — — — — — —
1000 1,000 1,000 1,000 — — — — — — — — — —

 

Таблица П4. Значения c 2 в зависимости от вероятности Р

и числа k степеней свободы

 

k

Вероятность Р
0,99 0.98 0,95 0,90 0,01 0,02 0,05 0,1
4 0,30 0,43 0,71 1,06 13,3 4,7 9,5 7,8
6 0,87 1,13 1,63 2,20 16,8 15,0 12,6 10,6
9 2,09 2,53 3,32 4,17 21,7 19,7 16,9 14,7
14 4,70 5,40 6,60 7,80 29,1 26,9 23,7 21,1
19 7,60 8,60 10,10 11,70 36,2 33,7 30,1 27,2
24 10,90 12,00 13,80 15,70 43,0 40,3 36,4 33,2
29 14,30 15,60 17,7 19,80 49,6 46,7 42,6 39,1

 

 

Таблица П5. Значения коэффициентов 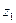 и 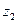 для доверительной

вероятности a = 0,95

 

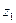
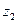
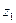
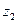
n n n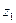
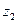
5 0,599 2,875 30 0,796 1,344 80 0,865 1,184
10 0,688 1,826 40 0,819 1,284 90 0,872 1,172
15 0,732 1,577 50 0,835 1,246 100 0,878 1,162
20 0,760 1,46 60 0,848 1,220 200 0,911 1,109
25 0,781 1,391 70 0,875 1,200 — — —

 

Таблица П6. Значения вероятностей Р (λ) для различных λ

 

l P(l) l P(l) l P(l) l P(l)
0,30 1,000 0,70 0,7112 1,20 0,1122 1,90 0,0015
0,35 0,9997 0,75 0,6272 1,30 0,0681 2,00 0,0007
0,40 0,9972 0,80 0,5441 1,40 0,0397 2,10 0,0003
0,45 0,9874 0,85 0,4653 1,50 0,0222 2,20 0,0001
0,50 0,9639 0,90 0,3927 1,60 0,0120 2,30 0,0001
0,55 0,9228 0,95 0,3275 1,70 0,0062 2,40 0,0000
0,60 0,8643 1,00 0,2700 1,80 0,0032 2,50 0,0000
0,65 0,7920 1,10 0,1777        

 

Таблица П7. Значения вероятностей Р для критерия c 2

c 2

k
1 2 3 4 5 6 7 8
1 0,3173 0,6055 0,8013 0,9098 0,9626 0,9856 0,9948 0,9982
2 1574 3679 5724 7358 8491 9197 9598 9810
3 0833 2231 3916 5578 7000 8088 8850 9344
4 0455 1353 2615 4060 5494 6767 7798 8571
5 0254 0821 1718 2873 4159 5438 6600 7576
6 0143 0498 1116 1991 3062 4232 5398 6472
7 0081 0302 0719 1359 2206 3208 4289 5366
8 0047 0183 0460 0916 1562 2381 3326 4335
9 0027 0111 0293 0611 1091 1736 2527 3423
10 0016 0067 0186 0404 0752 1247 1886 2650
11 0009 0041 0117 0266 0514 0884 1386 2017
12 0005 0025 0074 0174 0348 0620 1006 1512
13 0003 0015 0046 0113 0234 0430 0721 1119
14 0002 0009 0029 0073 0156 0296 0512 0818
15 0001 0006 0018 0047 0104 0203 0360 0591
16 0001 0003 00П 0030 0068 0138 0251 0424
17 0000 0002 0007 0019 0045 0093 0174 0301
18   0001 0004 0012 0029 0062 0120 0212
19   0001 0003 0008 0019 0042 0082 0149
20   0000 0002 0005 0013 0028 0056 0103
21   0000 0001 0003 0008 0018 0038 0071
22   0000 0001 0002 0005 0012 0025 0049
23   0000 0000 0001 0003 0008 0017 0034
24   0000 0000 0001 0002 0005 0011 0023
25   0000 0000 0001 0001 0003 0008 0016
26   0000 0000 0000 0001 0002 0005 0010
27   0000 0000 0000 0001 0001 0003 0007
28   0000 0000 0000 0000 0001 0002 0005

 

 

Таблица П8. Значения вероятностей 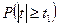| по распределению Стьюдента

t1

k
1 2 3 4 5 6 7 8 9 10 11 12
0,0 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000 1,000
0,1 0,937 0,929 0,927 0,925 0,924 0,924 0,923 0,923 0,923 0,922 0,922 0,922
0,2 874 860 854 851 849 848 847 846 846 845 845 845
0,3 814 792 784 779 776 774 773 772 771 770 770 759
0,4 758 782 716 710 706 703 701 700 698 698 697 696
0,5 705 667 651 643 638 635 632 631 629 628 627 626
0,6 656 609 591 581 575 570 567 565 563 562 561 560
0,7 611 556 534 523 515 510 507 504 502 500 498 497
0,8 570 508 482 469 460 454 450 447 444 442 441 439
0,9 533 463 434 419 409 403 398 394 392 389 387 384
1,0 500 423 391 374 363 356 351 347 343 341 339 337
1,1 470 385 352 333 321 313 308 303 300 297 295 293
1,2 442 353 316 296 284 275 269 264 261 258 255 253
1,3 417 323 284 263 250 241 235 230 226 223 220 218
1,4 395 296 256 234 220 211 204 199 195 192 189 187
1,5 374 272 231 208 194 184 177 172 168 165 162 159
1,6 356 251 208 185 170 161 154 148 144 141 138 136
1,7 339 231 188 164 150 140 133 128 123 120 117 115
1,8 323 214 170 146 132 122 115 110 105 102 099 097
1,9 308 198 154 130 116 106 099 094 090 087 084 082
2,0 295 184 139 116 102 092 086 081 077 073 071 069
2,1 283 171 127 104 090 080 074 069 065 062 060 058
2,2 272 159 115 093 079 070 064 059 055 052 050 048
2,3 261 148 105 083 070 061 055 050 047 044 042 040
2,4 251 138 096 074 062 053 047 043 040 037 035 034
2,5 242 130 088 067 054 047 041 037 034 031 030 028
2,6 234 122 080 060 048 041 035 032 029 026 025 023
2,7 226 114 074 054 043 036 031 027 024 022 021 019
2,8 218 107 068 049 038 031 027 023 021 019 017 016
2,9 281 101 063 044 034 027 023 020 018 016 014 013
3,0 205 095 058 040 030 024 020 017 015 013 012 011
3,1 199 090 053 035 027 021 017 015 013 011 010 009
3,2 193 085 048 036 024 019 015 013 011 009 008 008
3,3 187 081 045 030 021 016 013 011 009 008 007 006
3,4 182 077 042 027 019 014 011 009 008 007 006 005
3,5 177 073 039 025 017 013 010 008 007 006 005 004
3,6 172 069 037 023 016 011 009 007 006 005 004 004
3,7 168 066 034 021 014 010 008 006 005 004 004 003
3,8 164 063 032 019 013 009 007 005 004 003 003 003
3,9 160 060 030 018 011 008 006 005 004 003 002 002
4,0 156 057 028 016 010 007 005 004 003 003 002 002
4,1 152 055 026 015 009 006 005 003 003 002 002 001
4,2 149 052 025 014 008 006 004 003 002 002 001 001
4,3 145 050 023 013 008 005 004 003 002 002 001 001
4,4 142 048 022 012 007 005 003 002 002 001 001 001
4,5 139 046 020 011 006 004 003 002 001 001 001 001

 

 

Таблица П9. Значения Т для доверительной вероятности Р = 0,05

 

k2

k1 для большей дисперсии
1 2 3 4 5 6 8 12 24 ¥
1 161,45 199,50 215,72 224,57 230,17 233,97 238,89 243,91 249,04 254,32
2 18,51 19,00 19,16 19,25 19,30 19,33 19,37 19,41 19,45 19,50
3 10,13 9,55 9,28 9,12 9,01 8,94 8,84 8,74 8,64 8,53
4 7,71 6,94 6,59 6,39 6,26 6,16 6,04 5,91 5,77 5,63
5 6,61 5,79 5,41 5,19 5,05 4,95 4,82 4,68 4,53 4,36
6 5,99 5,14 4,76 4,53 4,39 4,28 4,15 4,00 3,84 3,67
7 5,59 4,74 4,35 4,12 3,97 3,87 3,73 3,57 3,41 3,23
8 5,32 4,46 4,07 3,84 3,69 3,58 3,44 3,28 3,12 2,93
9 5,12 4,26 3,86 3,63 3,48 3,37 3,23 3,07 2,90 2,71
10 4,96 4,10 3,71 3,48 3,33 3,22 3,07 2,91 2,74 2,54
11 4,84 3,98 3,59 3,36 3,20 3,09 2,95 2,79 2,61 2,40
12 4,75 3,88 3,49 3,26 3,11 3,00 2,85 2,69 2,50 2,30
13 4,67 3,80 3,41 3, 18 3,02 2,92 2,77 2,60 2,42 2,21
14 4,60 3,74 3,34 3,11 2,96 2,85 2,70 2,53 2,35 2,13
15 4,54 3,68 3,29 3,06 2,90 2,70 2,64 2,48 2,29 2,07
16 4,49 3,63 3,24 3,01 2,85 2,74 2,59 2,42 2,24 2,01
17 4,45 3,59 3,20 2,96 2,81 2,70 2,55 2,38 2,19 1,96
18 4,41 3,55 3, 16 2,93 2,77 2,66 2,51 2,34 2,15 1,92
19 4,38 3,52 3,13 2,90 2,74 2,63 2,48 2,31 2,11 1,88
20 4,35 3,49 3,10 2,87 2,71 2,60 2,45 2,28 2,08 1,84
21 4,32 3,47 3,07 2,84 2,68 2,57 2,42 2,25 2,05 1,81
22 4,30 3,44 3,05 2,82 2,66 2,55 2,40 2,23 2,03 1,78
23 4,28 3,42 3,03 2,80 2,64 2,53 2,38 2,20 2,00 1,76
24 4,26 3,40 3,01 2,78 2,62 2,51 2,36 2,18 1,98 1,73
25 4,24 3,38 2,99 2,76 2,60 2,49 2,34 2,16 1,96 1,71
26 4,22 3,37 2,98 2,74 2,59 2,47 2,32 2,15 1,95 1,69
27 4,21 3,35 2,96 2,73 2,57 2,46 2,30 2,13 1,93 1,67
28 4,20 3,34 2,95 2,71 2,56 2,44 2,29 2,12 1,91 1,65
29 4,18 3,33 2,93 2,70 2,54 2,43 2,28 2,10 1,90 1,64
30 4, 17 3,32 2,92 2,69 2,53 2,42 2,27 2,09 1,89 1,62
35 4,12 3,26 2,87 2,64 2,48 2,37 2,22 2,04 1,83 1,57
40 4,08 3,23 2,84 2,61 2,45 2,34 2,18 2,00 1,79 1,52
45 4,06 3,21 2,81 2,58 2,42 2,31 2,15 1,97 1,76 1,48
50 4,03 3,18 2,79 2,56 2,40 2,29 2,13 1,95 1.74 1,44
60 4,00 3,15 2,76 2,52 2,37 2,25 2,10 1,92 1,70 1,39
70 3,98 3,13 2,74 2,50 2,35 2,23 2,07 1,89 1,67 1,35
80 3,96 3,11 2,72 2,49 2,33 2,21 2,06 1,88 1,65 1,31
90 3,95 3,10 2,71 2,47 2,32 2,20 2,04 1,86 1,64 1,28
100 3,94 3,09 2,70 2,46 2,30 2,19 2,03 1,85 1,63 1,26
125 3,92 3,07 2,68 2,44 2,29 2,17 2,01 1,83 1,60 1.21
150 3,90 3,06 2,66 2,43 2,27 2,16 2,00 1,82 1,59 1,18
200 3,89 3,04 2,65 2,42 2,26 2,14 1,98 1,80 1,57 1,14
300 3,87 3,03 2,64 2,41 2,25 2,13 1,97 1,79 1,55 1,10
400 3,86 3,02 2,63 2,40 2,24 2,12 1,96 1,78 1.54 1,07
500 3,86 3,01 2,62 2,39 2,23 2,12 1,96 1.77 1,54 1,06
1000 3,85 3,00 2,61 2,38 2,22 2,10 1,95 1,76 1,53 1,03
¥ 3,84 2,99 2,60 2,37 2,21 2,09 1,94 1,75 1,52 ¥

 

 

Таблица П10. Критические значения G при 5%-ном уровне значимости

 

m - число выборок

n – 1  (п - объем выборок)
2 3 4 5 6 7 8 9
2 0,9975 0,9393 0,9056 0,8772 0,8534 0,8332 0,8139 0,8010
3 0,8709 0,7977 0,7457 0,7071 0,6771 0,6530 0,6333 0,6167
4 0,7679 0,6841 0,6278 0,5895 0,5598 0,5365 0,5175 0,5017
5 0,6838 0,5981 0,5441 0,5065 0,4763 0,4564 0,4387 0,4241
6 0,6161 0,5321 0,4803 0,4447 0,4184 0,3980 0,3817 0,3682
7 0,5612 0,4800 0,4307 0,3974 0,3726 0,3535 0,3384 0,3259
8 0,5157 0,4377 0,3910 0,3595 0,3362 0,3185 0,3043 0,2926
9 0,4775 0,4027 0,3584 0,3286 0,3067 0,2901 0,2768 0,2659
10 0,4450 0,3733 0,3311 0,3029 0,2823 0,2660 0,2541 0,2439
12 0,3924 0,3264 0,2880 0,2624 0,2439 0,2299 0,2187 0,2098
15 0,3346 0,2759 0,2419 0,2195 0,2034 0,1911 0,1815 0,1736
20 0,2705 0,2205 0,1921 0,1735 0,1602 0,1501 0,1422 0,1357

Таблица П11. Значение ρ 0 для величин λ 0

 

λ0 ρ0 λ0 ρ0 λ0 ρ0 λ0 ρ0 λ0 ρ0
1,3236 0,00 1,360 0,65 1,59 1,28 1,90 1,76 2,43 2,39
1,324 0,19 1,370 0,70 1,61 1,32 1,93 1,80 2,47 2,44
1,325 0,27 1,380 0,75 1,63 1,35 1,96 1,84 2,51 2,48
1,326 0,31 1,390 0,79 1,65 1,39 1,99 1,88 2,55 2,52
1,327 0,34 1,400 0,82 1,67 1,42 2,03 1,93 2,59 2,56
1,329 0,38 1,410 0,86 1,69 1,45 2,07 1,98 2,63 2,61
1,331 0,41 1,430 0,92 1,71 1,48 2,11 2,02 2,67 2,65
1,333 0,44 1,450 0,97 1,73 1,51 2,15 2,07 2,71 2,69
1,335 0,47 1,470 1,03 0,75 1,54 2,19 2,12 2,76 2,74
1,337 0,49 1,490 1,07 1,77 1,57 2,23 2,17 2,81 2,80
1,339 0,51 1,510 1,12 1,79 1,60 2,27 2,21 2,86 2,85
1,342 0,53 1,530 1,16 1,81 1,63 2,31 2,26 2,91 2,90
1,346 0,57 1,550 1,20 1,84 1,68 2,35 2,30 2,96 2,95
1,350 0,59 1,570 1,24 1,87 1,72 2,39 2,35 3,00 2,99

 

Таблица 12. Значения σ ρ для величин ρ 0

 

ρ0 σρ ρ0 σρ ρ0 σρ ρ0 σρ    
0,0 0,603 0,7 0,720 1,4 0,888 2,1 0,972 2,8 0,996
0,1 0,607 0,8 0,747 1,5 0,906 2,2 0,978 2,9 0,997
0,2 0,615 0,9 0,772 1,6 0,921 2,3 0,983 3,0 0,998
0,3 0,629 1,0 0,799 1,7 0,935 2,4 0,987    
0,4 0,647 1,1 0,824 1,8 0,947 2,5 0,990    
0,5 0,669 1,2 0,847 1,9 0,957 2,6 0,992    
0,6 0,694 1,3 0,869 2,0 0,966 2,7 0,994    

 

 


[1] В различных учебных пособиях по теории вероятностей и математической статистике для условной вероятности события B при условии, что произошло событие A, вместо обозначения P(B/A) применяют 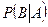 или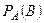

[2] Бородачев Н.А. Основные вопросы теории точности производства. М.-Л.: Изд-во АН СССР, 1950.

1. Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике. М.: Гостехиздат,1955.

[4] Энциклопедический справочник «Машиностроение». Том 15, М.: Машгиз, 1951.

[5] Бородачев Н.А. Анализ качества и точности производства. М., Машгиз, 1946.




Дата: 2019-02-25, просмотров: 222.

⇐ Предыдущая20212223242526272829
fb
inst
tw
vk
Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав. © 2018 - 2024