Статистическое управление процессами состоит в выявлении неслучайных нарушений процесса. При этом управляющее воздействие (регулирование) применяется тогда, когда выпускаемая продукция еще удовлетворяет заданным требованиям, но некоторые статистические показатели дают основание предполагать о наличии неслучайной причины, которая приведет к нарушению процесса.
На практике решение задачи статистического управления процессами осуществляют различными методами, один из которых основан на использовании контрольных карт У. Шухарта. Контрольная карта Шухарта, как инструмент оперативного статистического управления процессом, сигнализирует о разладке процесса, показывая выход контролируемого показателя за некоторую пороговую границу.
Контрольная карта Шухарта - графическое изображение мониторинга процесса. По горизонтальной оси откладываются моменты времени или номер измерения (выборки), по вертикальной - значения показателя качества. Проводятся также нижняя и верхняя контрольная границы (границы регулирования) и средняя линия. Если значение показателя оказалось на одной из контрольных границ или за ее пределами, то нулевая гипотеза о статистической управляемости процесса отклоняется и процесс требует вмешательства (регулировки).
Карты по количественному признаку применяются тогда, когда контролируемый показатель можно измерить. Это может быть, например, диаметр вала, шероховатость поверхности, прочность изделия, температура нагрева, электрическое сопротивление, вес изделия, влажность, содержание некоторого вещества в растворе и т.п.
Обычно контролируется изменение как среднего значения показателя качества, характеризующего уровень настройки процесса, так и технологического рассеивания, т. е. строятся двойные карты Шухарта. При этом уровень настройки процесса может оцениваться по средним значениям или медианам, а рассеивание - по стандартным отклонениям или размахам. В соответствии с этим чаще всего используются двойные карты следующих типов:
а) карты средних значений и размахов (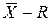 
-карты);
б) карты средних значений и стандартных отклонений (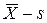 
-карты);
в) карты медиан и размахов (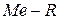 
-карты).
Процесс считается стабильным, или статистически управляемым, если об этом свидетельствуют обе карты - и для среднего уровня, и для рассеяния. Возможные состояния процесса с этой точки зрения показаны на рис. 3 (по ГОСТ Р 50779.44-2001).
Карта средних значений
Полагают, что показатель качества X имеет нормальное распределение со средним значением μ (характеризующим средний уровень настройки процесса) и стандартным отклонением σ (характеризующим технологическое рассеивание). Контроль процесса по уровню настройки состоит в том, чтобы обеспечить равенство среднего значения некоторому заранее заданному (целевому) уровню. Проверяется нулевая гипотеза Н0: μ = μ0 при альтернативе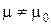 
.
Для построения контрольной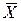 
-карты средних значений в определенные промежутки времени берутся мгновенные выборки - подгруппы (обычно объемом n от 3 до 10 единиц продукции) и определяется среднее значение показателя X в t-й выборке
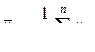, (1)
которое и откладывается на карте (xti - результат i-го наблюдения в t-й мгновенной выборке).
При определении границ регулирования учитывается, что если показатель X имеет нормальное распределение с математическим ожиданием μ и дисперсией σ2, то его среднее значение 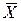также имеет нормальное распределение с математическим ожиданием μ и дисперсией 
.
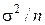На практике при определении границ регулирования часто используется правило «трех сигм», когда принимается уровень значимости α = 0,0027. В этом случае контрольные границы
. (2)
 |
Параметры технологического процесса μ0 и σ могут быть известны заранее из технических условий или оцениваются в ходе процесса. В последнем случае если, например, взято m мгновенных выборок, то оценка
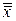среднего значения уровня настройки определяется по формуле
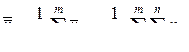. (3)
Для оценки технологического рассеивания σ вычисляется несмещенная оценка дисперсии каждой мгновенной выборки:
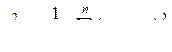(4)
и среднее квадратическое отклонение:
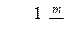. (5)
Величина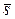 
является смещенной оценкой σ. Несмещенная оценка может быть определена по формуле
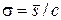, (6)
где значения коэффициента c приведены в таблице 1.
При построении контрольной карты вручную (без компьютера) с применением правила «трех сигм» удобно воспользоваться специальными таблицами. В этом случае формула (2) при известном α примет вид
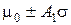, (7)
где коэффициент А1 определяется по таблице П6 в зависимости от объема мгновенной выборки п.
Часто при построении карты вручную проще оценить стандартное отклонение через размах R мгновенной выборки:
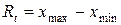; (8)
среднее значение размаха
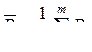. (9)
Тогда границы регулирования карты
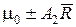. (10)
Как и при использовании в качестве характеристики рассеивания стандартного отклонения, величина R является смещенной оценкой σ, несмещенная оценка устанавливается из равенства
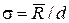, 11)
где значения d приведены в таблице 1.
При использовании оценки стандартного отклонения (5) границы карты средних значений определяются по формуле
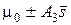. (12)
Коэффициенты А1, А2, А3 и другие в зависимости от объема мгновенной выборки п приведены в таблице 1.
На практике для принятия решения по контрольным картам в основном используется одно правило: процесс считается статистически управляемым тогда, когда определяемый по результатам измерений показатель лежит внутри контрольных границ.
Дата: 2019-02-25, просмотров: 215.
