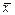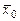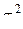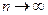1. Если объем выборки достаточно велик, то на основе закона больших чисел с вероятностью, как угодно близкой к достоверности, можно утверждать, что средняя арифметическая  и дисперсия s² выборки будут как угодно мало отличаться от генеральной средней  и генеральной дисперсии , т. е. , если , где n — объем выборки.

2. Ошибка вычисления генеральной средней 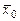 по средней  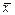выборки зависит от ее объема n и равна

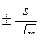.                                                        (1)

Ошибка вычисления среднего квадратического отклонения генеральной совокупности по среднему квадратическому отклонению выборки зависит от ее объема и равна

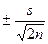.                                                        (2)

3. Если случайная величина х в генеральной совокупности имеет нормальное распределение со средней  и дисперсией 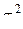, то и средние арифметические  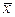выборок из этой совокупности будут подчинены также нормальному распределению со средней  и дисперсией 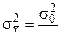, каков бы ни был объем выборок n, лишь бы число выборок было достаточно велико.

4. Когда дисперсия 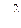 генеральной совокупности не известна, тогда для больших значений n с большей вероятностью малой ошибки можно дисперсию выборочных средних вычислять приближенно по равенству

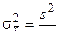,                                                   (3)

где s² — дисперсия большой выборки объема n, вычисляемая по формуле:

.

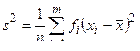5. Приведенная выше связь дисперсии выборочных средних с дисперсией генеральной совокупности 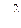 в виде соотношения

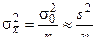
действительна для повторных выборок. Для бесповторных выборок эта связь выражается зависимостью

,

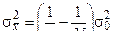где n — объем выборки; N — объем генеральной совокупности.

Если N по сравнению с n очень велико, что практически всегда имеет место, то для бесповторных выборок можно пользоваться для вычисления 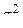 формулой (3), при этом ошибка будет весьма ничтожной.

Из свойств выборочных средних и дисперсий следует, что точность вычислений средних арифметических и дисперсий или средних квадратических отклонений генеральной совокупности по данным выборки из нее зависит от объема выборки, причем точность возрастает с ростом объема выборки. Однако практически не всегда бывает возможным или легко осуществимым взятие больших выборок или проведение большого числа наблюдений. Часто на практике приходится ограничиваться взятием небольших выборок или ограничиваться малым числом наблюдений. В этих случаях важно сделать оценку точности и надежности приближенных равенств

,

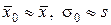где  - среднее арифметическое значение случайной величины генеральной совокупности; 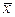 - то же в выборке объема п из генеральной совокупности; σ₀ - среднее квадратическое отклонение генеральной совокупности;

s - среднее квадратическое отклонение выборки.