Обозначим точность приближенного равенства 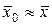 буквой ε. Тогда определение точности вычисления генеральной средней по данным выборки сведется к определению вероятности α того, что истинное значение  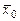находится в пределах 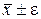, где ε > 0, т. е.

.

Для определения вероятности α пользуются распределением величины t:

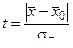.                                                 (4)

Если генеральная совокупность имеет нормальное распределение, то величина t при любом n распределена по закону Стьюдента, дифференциальная функция S_k(t) которого имеет следующее выражение

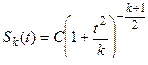,                                     (5)

где 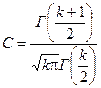 — постоянный множитель, зависящий только от числа степеней свободы k = п - 1. Символом Г(k) здесь обозначена гамма-функция (интеграл Эйлера):

.

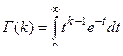Из выражения (5) следует, что распределение Стьюдента зависит только от переменной t и параметра k = n - 1. Поэтому когда задана вероятность α, то можно найти такое положительное число t_α которое будет зависеть только от α и n по равенству

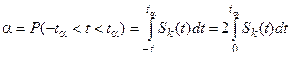.                         (6)

Учитывая, что 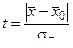, левую часть этого равенства можно преобразовать так:

.

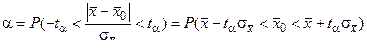Следовательно,

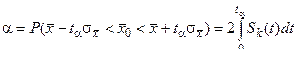                (7)

Полагая 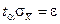, получим

.

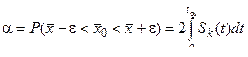Таблица значений t_α определяемых этим равенством, приведена в табл. П.2 приложения. При помощи этой таблицы можно определить одно из трех значений: вероятность α, точность ε или объем выборки п, задаваясь предварительно значениями каких-либо двух из этих величин.

Пример 1. По выборке объема n = 15 найдено 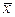= 20,4 и s = 0,8. Определить истинное значение генеральной средней .

Генеральная средняя 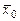 определяется доверительными границами

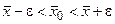, где .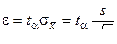

Зададимся надежностью α = 0,98. Тогда по таблице П.2 приложения при k = п - 1 = 14 находим t _а = 2,62. Поэтому

.

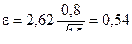Следовательно,

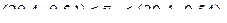, т. е. .

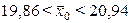Пример 2. Установить, какой объем n выборки необходимо взять, чтобы определить по этой выборке генеральную среднюю с точностью  и вероятностью α = 0,95.

Так как 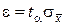, то, следовательно, t_α= 2. По таблице П.2 приложения для α = 0,95 находим значение t_α= 2, которому соответствует k = 60.

Поскольку k = п - 1, то п = 61.

Если n > 30, то распределение Стьюдента можно заменить нормальным и тогда

.                                      (8)

Но

,

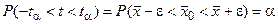следовательно,

.                                              (9)

Так как

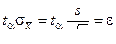,                                       (10)

то, обозначив 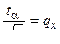, получим

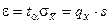.                                             (11)

Решая уравнение (10) относительно n, получим

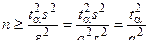.                                         (12)

Пример 3. Определить, какой должен быть объем выборки n, если желательно вычислить  с вероятностью α = 0,95 и точностью ε = 0,1s.

Согласно таблице П.1 приложения для α = 2Ф(t_α) = 0,95, t_α = 1,96. Следовательно, при 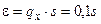 по формуле (12) имеем

.

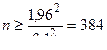Все изложенное об оценке точности и вероятности вычисления генеральной средней по выборочной средней является справедливым только для случаев, когда выборки берутся из генеральной совокупности, имеющей нормальное распределение случайной величины х или когда распределение х в генеральной совокупности не очень сильно отличается от нормального распределения. Если же распределение х в генеральной совокупности сильно отличается от нормального, то в этом случае вероятность α и точность ε приближенного равенства  можно определить только для больших выборок с помощью формул (9) и (10), но полученные значения α и ε не будут точными, а будут носить лишь приближенный характер.