На основании закона больших чисел можно утверждать, что если генеральная совокупность подчиняется определенному закону распределения, то и выборка из этой совокупности, если объем ее достаточно велик, будет подчиняться этому же закону. Утверждение будет тем точнее, чем больше объем выборки.

Всякую эмпирическую совокупность можно рассматривать как выборку большого объема из генеральной совокупности, подчиняющейся опреде-ленному теоретическому закону распределения. Следовательно, по характеру эмпирического распределения можно установить с определенной точностью и надежностью близкое ему теоретическое распределение. Зная закон, которому подчиняется данное распределение, можно использовать его для решения практических задач.

В ряде случаев тип закона можно установить заранее. Для этого необходимо проанализировать средствами теории вероятностей изучаемый процесс и подвести его, с некоторым приближением, к той или иной теоретической схеме. Например, основываясь на теореме Ляпунова, можно считать, что суммарная величина случайных погрешностей обработки при работе на настроенных станках при отсутствии действия какого-либо доминирующего фактора подчиняется закону нормального распределения. То же можно сказать о суммарной погрешности измерения, о средней высоте микронеровностей на обработанной поверхности и многих других технических величинах, подверженных колебаниям под действием большого количества случайных факторов.

В этих случаях, когда закон распределения заранее может быть установлен, задача сводится к нахождению неизвестных значений его параметров, т. е. к его параметризации. В случае нормального распределения задача сводится к установлению среднего арифметического значения изучаемой величины  и ее среднего квадратического отклонения σ₀.

Оценка параметров распределения генеральной совокупности может быть практически осуществлена только на основании данных выборки из этой совокупности.

Беря выборку из генеральной совокупности и вычисляя ее статистические характеристики 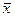 и s, можно с некоторым приближением считать, что они по своим величинам будут близки к соответствующим параметрам генеральной совокупности  и σ₀, т. е. являться их оценками. Но для того чтобы эти оценки достаточно правильно и близко характеризовали параметры генеральной совокупности, необходимо, чтобы они удовлетворяли трем требованиям: были бы состоятельными, несмещенными и эффективными.

Оценка называется состоятельной, если вероятность отклонения ее от оцениваемого параметра на величину, меньшую как угодно малого положительного числа ε, стремится к единице при неограниченном увеличении числа n наблюдений, т. е.

при ε > 0 и n→ ∞,

где θ — некоторый параметр генеральной совокупности; θ' — оценка этого параметра.

Оценка называется несмещенной, т. е. в ней отсутствуют систематические погрешности, если математическое ожидание этой оценки равно оцениваемому параметру

М(θ') = θ.

Если М(θ') > 0, то оценку называют положительно смещенной; если М(θ') < 0, то отрицательно смещенной.

Примером состоятельной и несмещенной оценки математического ожидания является средняя арифметическая. Примером состоятельной, но смещенной оценки теоретической дисперсии σ² может служить эмпирическая дисперсия s²

,

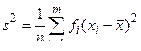где f_i - частота значений x_i; n - общее число наблюденных значений x_i, 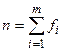; m - число отдельных значений x_i.

Для непрерывных случайных величин в качестве x_i принимают середину интервалов, на которые разбивается наблюденный ряд значений x.

Из выражения для оценки s² следует, что с увеличением n вероятность Р(| s² - σ² | < ε) → 1 и, следовательно, s² является состоятельной оценкой, но математическое ожидание 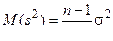 не равно σ² и при конечном n дает уменьшенное значение оцениваемого параметра σ², поэтому, оценивая σ² по s², мы допускаем систематическую ошибку, равную 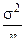, однако при больших n она пренебрежимо мала.

Для того чтобы получить несмещенную оценку теоретической дисперсии σ² по эмпирическим данным, необходимо эмпирическую дисперсию s² умножить на 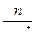, т. е.

.

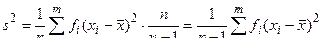Практически эту поправку вносят при вычислении оценки дисперсии в тех случаях, когда n < 30.

Состоятельных несмещенных оценок может быть несколько. Например, для оценки центра рассеивания нормального распределения, наряду со средней арифметической 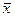, может быть взята медиана Ме. Медиана так же, как и 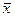, является несмещенной состоятельной оценкой центра группирования. Из двух состоятельных несмещенных оценок θ' и θ" для одного и того же параметра θ естественно отдать предпочтение той, у которой дисперсия меньше.

Такая оценка, у которой дисперсия будет наименьшей относительно θ, называется эффективной. Например, из двух оценок центра рассеивания нормального распределения эффективной оценкой является 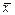, а не Ме, так как дисперсия  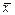меньше дисперсии Ме. Сравнительная эффективность Ме при большой выборке приближенно равна

.

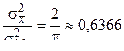Практически это означает, что центр распределения генеральной совокупности  определяется по медиане Ме с той же точностью при п наблюдениях, как при 0,6366 п наблюдениях по средней арифметической .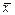

При решении задач, осуществляемых посредством выборочного метода, важное значение приобретают свойства выборочной средней и выборочной дисперсии, которые приведены ниже без доказательств.