Логарифмическое нормальное (логнормальное) распределение имеют характеристики усталостных испытаний материалов и устройств, износостойкости инструмента и др.

Логнормальное распределение – это распределение случайной величины x, распределение логарифма значений которой (t = lnx) подчиняется нормальному закону.

Дифференциальная функция распределения случайной величины x описывается следующим уравнением:

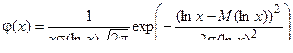,                          (34)

где 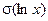 – среднее квадратическое отклонение логарифма случайной величины x;  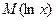- математическое ожидание логарифма случайной величины x.

Интегральная функция распределения вычисляется по формуле

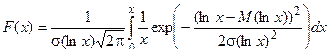.                  (35)

Контрольные вопросы

1. Распределение значений каких свойств изделий машиностроения, показатели которых являются случайными величинами, описывается биноминальным законом распределения? При каких условиях закон биномиального распределения и закон редких событий практически совпадают?

2. Какие статистические характеристики используются при описании распределения случайной величины нормальным законом?

3. Каким законом может быть описано распределение случайной величины, характеризующей биение обрабатываемой поверхности?

4. Каким законом может быть описано распределение погрешности формы деталей: овальность, конусность?

5. Распределение каких случайных величин могут быть описаны законом Вейбулла-Гнеденко? Приведите интегральную функцию этого закона распределения случайной величины.

Лекция 3

Тема. Выборочный метод

1. Основные понятия и определения теории выборок.

Одной из основных задач математической статистики является разработка методов изучения массовых явлений или процессов на основе сравнительно небольшого количества наблюдений или опытов. Эти методы имеют свое научное обоснование, свою теорию, которая носит название теории выборок. При изучении основных положений этой теории приходится встречаться с рядом новых понятий и определений, с которыми необходимо предварительно познакомиться.

Генеральная совокупность и выборка из нее. Группа предметов, объединенных каким-либо общим признаком или свойством качественного или количественного характера, носит название статистической совокуп-ности. Например, партия деталей представляет собой статистическую совокупность. Признак, по которому детали объединяются в совокупность, может быть количественным (размер) или качественным («брак», «не брак»). Следовательно, одни и те же предметы могут образовывать несколько совокупностей в зависимости от того, по какому признаку они объединяются в совокупность: количественному или качественному.

Предметы, образующие совокупность, называются ее членами. Общее число членов совокупности составляет ее объем. Если совокупность содержит конечное число членов, полученных в результате испытаний, то она называется эмпирической.

Эмпирическая совокупность может состоять из очень большого числа членов, изучение или обследование которых представляет весьма трудоемкую задачу. В математической статистике для обследования большой совокупности прибегают к выборкам из нее.

Выборкой называется часть членов совокупности, отобранных из нее для получения сведений о всей совокупности. В этом случае совокупность, из которой извлекается выборка, называется генеральной совокупностью.

Число членов, образующих выборку, составляет ее объем. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы члены выборки правильно его представляли. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной).

Виды выборок. По способу образования выборки делятся на повторные и бесповторные. Повторная выборка образуется путем последовательного извлечения из генеральной совокупности нескольких членов с возвратом каждого из них после соответствующего обследования обратно в генеральную совокупность. При извлечении следующего объекта из совокупности не исключена возможность снова вынуть этот же объект. Если из генеральной совокупности произведено n таких извлечений объекта, то говорят, что образована повторная выборка объема n. Например, из партии в 1000 шт. деталей последовательно извлекается 10 деталей в следующем порядке: извлекается первая деталь и измеряется, затем она возвращается в совокупность, последняя перемешивается, затем извлекается вторая деталь, производится ее измерение, снова деталь возвращается в совокупность, последняя перемешивается, извлекается следующая деталь и т. д. Извлеченные таким способом 10 деталей составят повторную выборку объемом в 10 шт.

Бесповторная выборка образуется путем извлечения некоторого числа членов генеральной совокупности для необходимого обследования без возврата этих членов в совокупность. Например, если из партии в 1000 шт. деталей сразу или последовательно будет извлечено 10 деталей без возвращения их обратно, то будет образована бесповторная выборка объемом в 10 шт.

Выборки, кроме указанных, делятся также на преднамеренные и случайные, мгновенные и общие, малые и большие.

Выборка считается преднамеренной, если отбор объектов для нее из генеральной совокупности производится с определенной тенденцией, приводящей к повышению или понижению вероятности выявления изучаемого признака качества.

Выборка считается случайной, если все объекты генеральной совокупности имеют равную возможность попасть в выборку. Для образования случайных выборок пользуются либо отбором по жребию, либо путем тщательного перемешивания предметов в ящике и отбора их наудачу из разных мест ящика.

Мгновенной (или текущей) выборкой называется выборка малого объема, взятая из числа единиц потока продукции, изготовленных к моменту отбора в короткий промежуток времени, в котором проявление систематических погрешностей пренебрежимо мало.

Общей выборкой называется выборка, состоящая из серии мгновенных выборок.

Малой выборкой считается выборка, объем которой меньше 25 членов. Если объем выборки больше 25 членов, то она считается большой. В производственных исследованиях обычно большая выборка состоит из 50-100 или более членов, а малая выборка из 5-10 членов.

Задачи выборочного метода. Выборочный метод позволяет решить две основные задачи, имеющие большое практическое значение. Первая задача заключается в установлении закона распределения изучаемой случайной величины и определения параметров этого распределения по данным выборки, вторая — в статистической проверке гипотез, выдвигаемых при различных производственных исследованиях.

В этой теме кратко рассмотрена сущность первой задачи выборочного метода.