Вспомним, что совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей, называется распределением случайных величин. При наличии определенных условий распределения случайных величин могут подчиняться вполне определенным законам. Законы распределения случайных величин изучаются в теории вероятностей. Из этих законов наибольшее практическое значение в машиностроении имеют:

- для дискретных случайных величин: закон биноминального распределения и закон редких событий;

- для непрерывных случайных величин: закон равной вероятности, закон нормального распределения, закон эксцентриситета, закон экспоненциального распределения, закон распределения Вейбулла-Гнеденко, закон логарифмического нормального распределения и закон распределения модуля разности.

1. Закон биноминального распределения.

Закон биноминального распределения используется при оценке качества и надежности изделий.

Пусть производится серия последовательных независимых испытаний, каждое из которых заканчивается одним из двух несовместных между собой результатов: или событие A наступает, или оно не наступает. Вероятность появления события A в каждом испытании равна p, а вероятность не появления события A равна q = 1 - p. Так как испытания независимы, то вероятность появления или не появления события A не зависит от результатов предыдущих испытаний. При такой схеме испытаний вероятность появления события A заданное число раз подчиняется закону биномиального распределения, который можно сформулировать так: если вероятность события A постоянна в серии последовательных независимых испытаний и равна p, то вероятность появления события A ровно k раз в п испытаниях будет равна

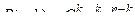                                  (1)

где k -число появления события ; n - число независимых испытаний.

Это уравнение определяет собой распределение вероятностей случайного числа k, которое называется биномиальным.

В формуле (1) символ 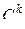 обозначает число сочетаний из n элементов по k, т. е. биномиальный коэффициент. Биномиальный коэффициент вычисляется по формуле

,

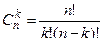где символ n! обозначает факториал и выражает произведение натуральных чисел 1, 2, 3,. . ., n. При этом 0! = 1. С учетом изложенного формула (1) примет вид:

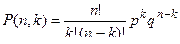.                             (2)

Закон биномиального распределения двухпараметрический, в котором математическое ожидание M(k) и дисперсия 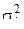 равны:

M(k) = np; 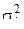 = npk.

Пример 1. В партии деталей имеется брак, доля которого составляет 0,1. Производится последовательное извлечение 10 деталей. После каждого извлечения и обследования детали она вновь возвращается в партию, которая затем тщательно перемешивается, т.е. испытания носят независимый характер. Какова вероятность того, что при извлечении по такой схеме 10 деталей среди них появится одна бракованная?

Решение. Очевидно, что вероятность извлечения бракованной детали составляет p = 0,1, вероятность противоположного события - извлечение годной детали q = 1 - p = 0,9. Число испытаний n = 10 и k = 1. Следовательно, по формуле (2) находим

.

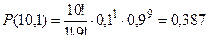Полученный результат можно отнести и к тому случаю, когда извлекается подряд 10 деталей без возврата их обратно в партию и объем партии достаточно велик. При достаточно большой партии, например 1000 шт., вероятность извлечения годной или негодной детали после каждого из 10 извлечений деталей изменится ничтожно мало. Поэтому при таких условиях извлечение бракованной детали можно рассматривать как событие, не зависящее от результатов предшествующих испытаний.

Пример 2. На участке имеется пять одинаковых станков, коэффициент использования которых по времени составляет 0,8. Какова вероятность того, что в середине смены при нормальном ходе производства из пяти таких станков будет работать только два, а три не работать?

Решение. Так как p = 0,8; q = 0,2; n = 5 и k = 2, то

.

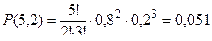2. Закон редких событий (Пуассона)

Если вероятность p события A очень мала (p ≤ 0,1), а число n испытаний велико, то вероятность того, что событие A наступит k раз в n испытаниях, будет равна

,                                      (3)

где а = np = M(k) — математическое ожидание числа k.

Уравнение (3) определяет собой распределение редких событий, или распределение Пуассона.

Когда число испытаний n велико, а p мало, то закон биномиального распределения и закон редких событий практически совпадают. Это имеет место тогда, когда p ≤ 0,1 и np < 4. При этих условиях вместо формулы (2) можно применить формулу (3), т. е.

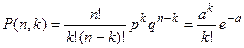.                         (4)

Принимая во внимание, что a = np , формула (4) примет вид

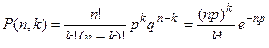.                      (5)

Пример 3. В партии деталей имеется 1% брака. Какова вероятность того, что при взятии из партии выборки объемом 50 шт. в ней будет находиться 0, 1, 2, 3, 4 дефектных детали.

Решение. Учитывая, что p = 0,01; n = 50, находим:

np = 50 0,01 = 0,5;

; ;

; ; .

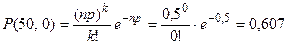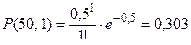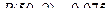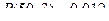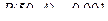Закон Пуассона имеет только один параметр М(k) = а = np. Для этого распределения дисперсия численно равна математическому ожиданию: 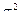 = M(k). Поэтому, когда в распределении дискретной случайной величины  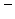и σ² мало отличаются друг от друга по своим численным значениям, то можно уверенно считать, что данное распределение подчиняется закону редких событий.

Закон редких событий имеет практическое применение в машиностроении для выборочного контроля готовой продукции, когда по техническим условиям в принимаемой партии продукции допускается некоторый процент брака (обычно небольшой) и поэтому всегда p << 0,1, а объем выборки n берут таким, чтобы было np << 4.

При помощи закона редких событий можно вычислить вероятность того, что в выборке из n шт. будет содержаться: 0, 1, 2, 3 и т. д. бракованных деталей, т. е. заданное число k раз. Можно также вычислить вероятность появления в такой выборке k штук дефектных деталей и более. Эта вероятность на основании правила сложения вероятностей будет равна

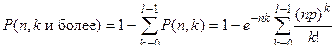,               (6)

где k = 0,1,2,...,l.

Если эта вероятность для некоторого значения k окажется очень малой (например, меньше 0,05), то на основании принципа практической невозможности маловероятных событий можно считать, что появление в выборке из n штук деталей k или более дефектных несовместимо с нашим исходным допущением, что во всей партии имеется не более 100р % брака. Следовательно, в действительности во всей партии имеется брак более чем 100р %, и она не может быть принята.

Пример 4. Допустимый процент брака во всей партии составляет 1%, т. е. p = 0,01. Объем выборки n = 50. Определить вероятность того, что в выборке окажется 1, 2, 3 и более дефектных деталей.

Решение. Определим сначала вероятности того, что в выборке окажется 0, 1, 2, 3 и т. д. дефектных деталей.

Из предыдущего примера имеем:

Р(50,0) = 0,607; Р(50,1) = 0,303; Р(50,2) = 0,075;

Р(50,3) = 0,012; Р(50,4) = 0,001.

Отсюда

Р(50,1 или более) = 1 - 0,607 = 0,393;

Р(50,2 или более) = 1-(0,607+0,303) = 0,393-0,303 = 0,09;

Р(50,3 или более) = 0,090 - 0,075= 0,015;

Р(50,4 или более) = 0,015 - 0,012 = 0,003.

Следовательно, если в выборке обнаружится 3 или более дефектные детали, то в силу малой вероятности такого явления (Р = 0,015) надо считать, что во всей партии в действительности доля брака более чем 0,01.