Случайной величиной называется переменная величина, которая в результате испытаний (опытов) может принять то или иное значение в границах определенного интервала. Например, действительный размер детали, обработанной на станке, является случайной величиной, так как он может принять любое численное значение в определенных пределах.
Случайные величины подразделяются на дискретные и непрерывные.
Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные, большей частью целочисленные значения, и не могут принимать значения, промежуточные между ними. Например, количество негодных деталей в партии может быть только целым положительным числом 1,2, 3 и т. д., но не может быть 1,1; 1,4 и т. п. Следовательно, количество негодных деталей есть случайная величина дискретного типа.
Непрерывной случайной величиной называется такая, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала. Например, действительные размеры деталей, обработанных на станке, являются случайными величинами непрерывного типа, так как они могут принять любое численное значение в определенных границах.
Возможности случайных величин принимать при испытаниях те или иные численные значения оцениваются при помощи вероятностей.
Совокупность значений случайной величины, расположенных в возрастающем порядке с указанием их вероятностей, называется распределением случайной величины. Различают теоретические и эмпирические распределения случайных величин.
В теоретических распределениях оценка возможных значений дискретной случайной величины производится при помощи вероятностей, а в эмпирических — при помощи частот или частостей, полученных в результате опытов или испытаний.
Распределения случайных величин дискретного типа можно представить в табличной форме (табл. 1, 2) или в виде графика (рис. 1).
Таблица 1. Теоретическое распределение дискретной случайной величины
| 
| 
| 
| 
| … | 
| |
| 
| 
| 
| 
| … | 
| 
|
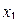
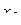
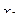
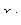
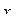
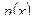
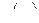
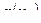
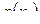
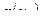
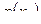
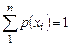
Пример 10. Проверены 32 партии деталей на наличие в них бракованных деталей. Результаты проверки партий приведены в табл. 2, в которой через x обозначено число бракованных деталей в одной партии, через mx - частость наличия x бракованных деталей в партии.
Таблица 2. Эмпирическое распределение дискретной случайной величины
| x | 0 | 1 | 2 | 3 | 4 | 5 | |
| 
| 
| 
|
| 
| 
| 
|
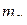
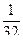
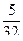
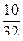
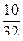
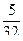
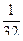
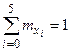
Если случайная величина является непрерывной, то возникает затруднение представить ее распределение в виде таблицы или графика, даже если значения случайной величины лежат в весьма узком интервале. Поэтому на практике при изучении случайных величин непрерывного типа их полученные значения разбивают на интервалы (разряды) с таким расчетом, чтобы величина интервала была несколько больше цены деления шкалы измерительного инструмента и таким образом компенсировалась бы погрешность измерений. Затем подсчитывают частоты не по действительным значениям случайной величины, а по интервалам, т. е. имеют дело не с частотами наблюденных значений случайной величины непрерывного типа, а с частотами их значений, лежащих в границах установленного интервала. Поэтому таблица эмпирического распределения случайной величины непрерывного типа будет иметь вид табл. 3.
Эмпирическое распределение случайной величины непрерывного типа (см. табл. 3) может быть представлено в виде ступенчатого графика или в виде ломаной кривой (рис. 2). Ступенчатый график называется гистограммой распределения, а ломаная кривая — полигоном распределения или эмпирической кривой распределения.
Таблица 3. Эмпирическое распределение случайной величины непрерывного типа
| Интервалы значений x | Частота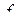 
| Частость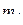 
|
| 20,00—20,05 | 2 | 0,02 |
| 20,05—20,10 | 10 | 0,10 |
| 20,10—20,15 | 24 | 0,24 |
| 20,15—20,20 | 30 | 0,30 |
| 20,20—20,25 | 22 | 0,22 |
| 20,25—20,30 | 10 | 0,10 |
| 20,30—20,35 | 2 | 0,02 |
| 
|
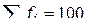
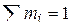
При теоретическом изучении случайных величин непрерывного типа используется понятие функции распределения.
Пусть X — случайная величина, а x — какое-либо действительное число, при этом X < x и этому событию отвечает вероятность P(X < x), которая, очевидно, является функцией х, т.е. P(X < x) = F(x).
F(x) называется функцией распределения вероятностей случайной величины или интегральной функцией распределения. Таким образом, интегральная функция распределения определяет вероятность того, что случайная величина X при испытаниях примет значение меньше произвольно изменяемого действительного числа x (- ∞ < x < + ∞). Случайная величина считается заданной, если известна ее функция распределения.
Для дискретной случайной величины интегральная функция распределения F(x) легко определяется по таблице или графику распределения. Например, по графику (см. рис. 1) F(x) для любого значения х равна сумме вероятностей тех значений X, которые лежат левее точки x. В частности, для X < 3:
.
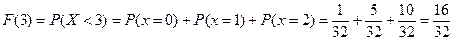Интегральную функцию распределения можно представить в виде графика, если по оси абсцисс откладывать значения х, а по оси ординат — значения F(x) = P(X < x). Для дискретной случайной величины график интегральной функции распределения будет иметь вид ступенчатой кривой. Для распределения согласно табл. 2 этот график будет иметь вид, изображенный на рис. 3. Ординаты кривой для любого значения х будут представлять сумму вероятностей предшествующих значений
F(x) = P(X < x).
Если известны F(x1) и F(x2), т. е. ординаты интегральной кривой для двух произвольных точек, взятых на оси абсцисс, то известны и вероятности событий, заключающихся в том, что значения случайной величины X при испытаниях окажутся меньше, чем x1 или x2, так как
F(x1) = P(X < x1); F(x2) = P(X < x2).
Зная эти вероятности, можно вычислить и вероятность того, что при испытаниях случайная величина окажется в границах от x1 до x2 (включая x1 и исключая x2), т. е.
P(x1 ≤ X < x2).
Очевидно, что событие X < x2 распадается на два частных события:
X < x1 и x1 ≤ X < x2.
На основании правила сложения вероятностей
P(X < x2) = P(X < x1) + P(x1 ≤ X < x2).
Откуда
P(x1 ≤ X < x2) = P(X < x2) - P(X < x1) = F(x2) - F(x1).
Таким образом, вероятность того, что случайная величина при испытаниях окажется в границах от x1 до x2, равна приращению интегральной функции распределения на этом участке.
Для непрерывной случайной величины график интегральной функции распределения будет иметь вид не ступенчатой, а монотонно возрастающей кривой, имеющей касательную к каждой точке (рис. 4).
Возьмем на оси абсцисс две произвольные точки x0 и x0 + Δx. Ординаты функции в этих точках будут F(x0) и F(x0 + Δx). По аналогии с предыдущим
P(x0 ≤ X < x0 + Δx) = F(x0 + Δx) - F(x0).
 |
Интегральная функция распределения непрерывной случайной величины является дифференцируемой функцией. Первая производная от интегральной функции называется дифференциальной функцией распределения, или плотностью вероятности.
Будем обозначать ее через φ(x). Исходя из определения производной, можно, написать
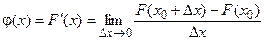
или, учитывая равенство (1),
.
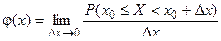Таким образом, плотность вероятности φ(x) есть предел отношения вероятности того, что случайная величина X при испытаниях примет значение, лежащее в границах от x0 до x0 + Δx к величине интервала Δx, когда величина Δx стремится к нулю. F(x) является первообразной функцией по отношению к φ(x), поэтому вероятность того, что случайная величина X при испытаниях примет значение, лежащее в границах от a до b, равна определенному интегралу в пределах от a до b от плотности вероятности:
.
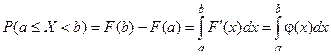Дифференциальную функцию распределения непрерывной случайной величины, можно выразить в виде кривой, имеющей ту или иную форму. Например, при выполнении определенных условий дифференциальная функция распределения φ(x) непрерывной случайной величины может иметь вид холмообразной кривой (рис. 5). В данном случае вероятность
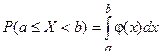
будет представлять площадь криволинейной трапеции с основанием ab, ограниченной сверху дифференциальной кривой распределения. Это следует из
.
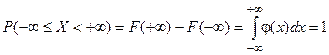3. Числовые характеристики распределений случайных величин.
Для изучения распределений случайных величин в математической статистике пользуются рядом числовых характеристик, определяющих положение центра группирования случайной величины и ее рассеивание около этого центра. Числовые характеристики положения центра группирования носят общее название мер положения, а числовые характеристики рассеивания — мер рассеивания.
В качестве мер положения используются математическое ожидание, среднее арифметическое значение, медиана и мода, в качестве мер рассеивания— дисперсия, среднее квадратическое отклонение и размах.
Математическим ожиданием M(x) дискретной случайной величины x называется сумма произведений всех m ее возможных значений xi на их вероятности p(xi)
.
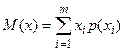Для непрерывной случайной величины ее математическое ожидание M(x) определяется по формуле
,
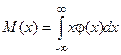где φ(x) плотность вероятностей величины x.
Математическое ожидание обычно используется в качестве меры положения для теоретических распределений (где используется так называемая генеральная совокупность объектов), в которых возможные значения x оцениваются при помощи вероятностей. В эмпирических распределениях, где наблюденные значения x оцениваются при помощи частот или частостей, в качестве меры положения используется среднее арифметическое 
.
- среднее арифметическое значение случайной величины x
.
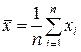При большом числе n полагают, что среднее арифметическое значение случайной величины x приближенно равно ее математическому ожиданию:
.
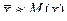Среднее арифметическое значение случайной величины может быть вычислена как сумма произведений наблюденных значений случайной величины на их частости:
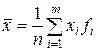
где fi - частота значений xi;
n - общее число наблюденных значений xi,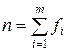 
;
m - число отдельных значений xi.
Для непрерывных случайных величин в качестве xi принимают середину интервалов, на которые разбивается наблюденный ряд значений x.
Основные свойства математического ожидания. Математическое ожидание, а также и среднее арифметическое значение обладают рядом свойств, которые выражены в теоремах о математическом ожидании. Приведем эти теоремы без доказательств.
1. Математическое ожидание постоянной C есть сама эта постоянная:
М(C) = С.
2. Математическое ожидание произведения постоянной величины С на случайную величину х равно произведению постоянной на математическое ожидание случайной величины
M(Cx) = CM(x).
3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин
.
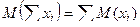4. Математическое ожидание суммы постоянной и случайной величины равно сумме постоянной величины и математического ожидания случайной величины
M(C + x) = C + M(x).
5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
M(xy) = M(x)·M(y).
Медианой непрерывной случайной величины называется такое ее значение, для которой функция распределения равна 0,5. Это означает, что вероятность случайной величины х принять значение, меньшее медианы, в точности равна вероятности этой величины принять значение, большее медианы. Медиана обозначается символом Me и для непрерывной случайной величины определяется из соотношения
.
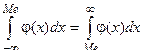Геометрически медиана является абсциссой такой точки кривой плотности вероятности φ(х), ордината которой делит площадь под кривой на две равновеликие части (рис. 6).
Если случайная величина x дискретного типа, то для определения медианы значения х располагают в порядке возрастания их величин (x1, x2, x3,…, xm,…, xn) и в качестве медианы принимают такое срединное значение x между x m-1 и xm, чтобы удовлетворялось условие
.
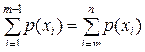Аналогичным образом определяется и эмпирическое значение медианы. Например, со станка взято 5 деталей с размерами: 20,10; 20,05; 19,98; 20,08; 20,03. Расположим полученные размеры в порядке возрастания: 19,98; 20,03; 20,05; 20,08; 20,10. При нечетном числе данных берут в качестве медианы число, занимающее срединное положение, т. е.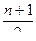 
по порядку, в данном примере при n = 5 третье: Me=20,05. Если число данных n четное, то в качестве медианы берут среднее арифметическое из двух членов, занимающих срединное положение. Например, при n = 4
.
 |
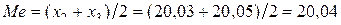Модой Mo называется такое значение случайной величины x, которое имеет наибольшую вероятность p(x) для распределения дискретной случайной величины или наибольшую плотность вероятности φ(x) для распределения непрерывной случайной величины. Если кривая распределения имеет два или несколько одинаковых максимумов, то она называется соответственно двухмодальной или многомодальной (рис. 7). Если максимумы резко выражены, но различны по величине, то кривая называется многовершинной (рис. 8). Если в центральной части кривой распределения имеется минимум, по обе стороны от которого происходит непрерывное возрастание кривой до границ области значений случайной величины, то такая кривая называется антимодальной (рис. 9).
Все перечисленные характеристики M(x), 
, Me, Mo определяют положение центра группирования случайных величин в данном распределении. Около этого центра сосредоточивается наибольшее количество значений изучаемой величины. По мере удаления от центра группирования (влево и вправо) число значений случайной величины убывает. Между перечисленными характеристиками положения центра группирования нет определенных соотношений. Это ясно без всяких пояснений в отношении M(x), Me и Mo.
Что касается M(x) и 
, то по своему существу они равноценны и область применения их была указана выше. При симметричных одномодальных распределениях значения всех характеристик положения центра группирования (M(x), Me, Mo) равны между собой (рис. 10). Размерности всех перечисленных характеристик совпадают с размерностью случайной величины.
 |
Меры рассеивания. Для характеристики распределения случайной величины недостаточно знать только положение центра группирования, так как оно не характеризует разброс или рассеивание различных значений случайной величины около центра. Необходима числовая характеристика, показывающая, насколько тесно сгруппированы возможные значения случайной величины около центра группирования. Такая характеристика называется мерой рассеивания. В технике наиболее употребительными мерами рассеивания являются: дисперсия, обозначаемая символами D(x), σ2 или s2, среднее квадратическое отклонение, обозначаемое через символы σ или s, и размах, обозначаемой символом R.
Дисперсией (рассеянием) возможных значений xi случайной величины x около ее математического ожидания M(x) называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
.
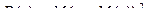Дисперсия дискретной случайной величины непосредственно вычисляется по формуле
.
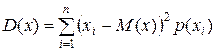Для непрерывной случайной величины дисперсия определяется по формуле
.
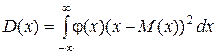Для эмпирического распределения дисперсию обозначают через σ2 или s2 и определяют по формуле
при n > 30
,
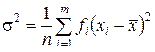при n < 30
.
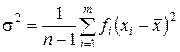Дисперсия имеет размерность, представляющую собой квадрат размерности самой случайной величины. На практике это неудобно. Поэтому в технике чаще пользуются не самой дисперсией, а корнем квадратным из нее, взятым со знаком плюс и называемым средним квадратическим отклонением:
.
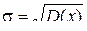или для эмпирических распределений
.
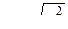Размерность σ совпадает с размерностью самой случайной величины х.
Размахом, или широтой распределения пользуются как мерой рассеивания в эмпирических распределениях при малом числе наблюдений, когда п < 10. Размахом называется разность между наибольшим и наименьшим наблюденными значениями случайной величины:
.
Основные свойства дисперсий и средних квадратических отклонений. Дисперсии и средние квадратические отклонения обладают рядом свойств, вытекающих из теорем о дисперсиях. Приводим эти свойства без доказательств.
1. Дисперсия постоянной величины с равна нулю:
Dc = 0.
2. Дисперсия произведения постоянной величины с на случайную величину х равна произведению квадрата постоянной величины с на дисперсию случайной величины х:
Dcx = c2Dx.
3. Дисперсия суммы постоянной c и случайной величины x равна дисперсии случайной величины x:
D(c + x) = Dx.
4. Дисперсия суммы нескольких независимых случайных величин х1, х2,- , хn равна сумме дисперсий этих величин:
.
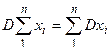Контрольные вопросы .
1. Приведите задачи дисциплины «Математическая статистика в технологии машиностроения». Какие методы математической статистики применяются при решении задач в области технологии машиностроения?
2. Что количественно оценивает вероятность случайного события, являющегося результатом осуществления какого либо комплекса условий? Как находится вероятность, например, события A. В чем отличие частоты события А и частости этого события?
3. Поясните на примерах требования к двум и более событиям: «Они должны быть равновозможны, несовместны и независимы». Что понимают под условной вероятностью события B (или A), если события A и B зависимы?
4. Сформулируйте правило сложения вероятностей несовместных случайных событий А, В и С.
5. Сформулируйте правила умножения вероятностей независимых и зависимых случайных событий А, В и С.
6. Дайте определение интегральной функции распределения вероятностей случайной величины. Какие значения она может принимать?
7. Что собой представляет в математическом смысле дифференциальная функция распределения? Почему эту функцию называют плотностью вероятности (или плотностью распределения вероятностей непрерывной случайной величины) и как можно интерпретировать плотностью вероятности с физической точности зрения?
8. Какие числовые характеристики распределения случайных величин относятся к мерам положения, и какие к мерам рассеивания?
9. В чем отличие медианы от моды распределения случайной величины?
10. Как можно геометрически истолковать понятие среднего квадратического отклонение случайной величины?
Лекция 2
Дата: 2019-02-25, просмотров: 215.
