Из классического определения вероятности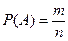 
вытекают следующие ее свойства:
1. Вероятность достоверного события А1 равна единице:
.
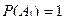Так как число случаев m, благоприятствующих достоверному событию, равно числу всех возможных случаев п, т. е. т = п; следовательно,
.
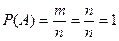2. Вероятность невозможного события А2 равна нулю
P(A2)=0,
так как невозможному событию не благоприятствует ни один из n возможных случаев, т. е. т = 0, и, следовательно,
.
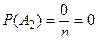3. Вероятность случайного события А3 заключена между нулем и единицей, так как в этом случае 0 < m < п, а значит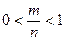 
; следовательно, 0 < Р(A3)< 1. Вероятность любого события А определяется неравенством
0 < Р(А)< 1.
Правило сложения вероятностей. Вероятности случайных событий или величин можно складывать и умножать. Если события А, В и С несовместны, т. е. появление любого из них исключает возможность появления другого и вероятность появления каждого соответственно равна Р(А), Р(В), Р(С), то вероятность осуществления какого-либо из этих несовместных событий (A или В или С) равна сумме их вероятностей, т. е. [2]
Р(А или В или С) = Р(А) + Р(B) + Р(С).
В учебном пособии [1] сумма вероятностей Р(А), Р(В), Р(С) событий А, В и С обозначается в виде Р(А + В + С).
Пример 3. В партии из 100 деталей имеется 6 с заниженными против допуска размерами и 4 с завышенными. Найти вероятность извлечения негодной детали, т. е. с завышенным или заниженным размером.
Решение. Вероятность события А, заключающегося в извлечении детали с заниженными размерами, составляет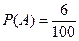 
. Вероятность события В — извлечение детали с завышенным против допуска размером 
.
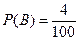Вероятность извлечения негодной детали составляет
.
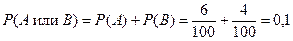Из правила сложения вероятностей вытекают два следствия:
1. Сумма вероятностей противоположных событий равна единице. Если обозначим вероятность осуществления какого-либо события через р, а вероятность его неосуществления через q, то
р + q=1,
так как достоверно, что оно либо осуществится, либо нет.
2. Вероятность противоположного события равна дополнению до единицы к вероятности данного события, т. е.
q = 1 – p.
Например, в ящике 90 годных деталей и 10 негодных. Вероятность извлечения годной детали р = 0,9. Вероятность противоположного события - извлечения негодной детали
q = 1 - р = 1 - 0,9 = 0,1.
Правило умножения вероятностей. Произведением двух событий A и B называют событие AB, состоящее в совместном появлении (совмещении) этих событий. Например, если A – деталь годная, B – деталь окрашенная, то AB – деталь годная и окрашенная.
Произведением нескольких событий A, B, C называют событие ABC, состоящее в совместном появлении всех этих событий. Например, A, B, C - наличие одной бракованной детали соответственно в первой, во второй и в третьей проверяемых партиях деталей, то ABC – во всех трех партиях деталей есть одна бракованная.
Условная вероятность. Как отмечено выше, события могут быть независимыми и зависимыми. К независимым относятся такие события, вероятность появления каждого из которых не зависит от появления или непоявления любых других событий этого класса. Если же вероятность появления одного из событий данного класса изменяется от появления или непоявления других событий этого же класса, то такие события называются зависимыми.
Например, если в партии деталей имеется несколько штук негодных деталей, то извлечение негодной детали будет независимым событием при условии, что после каждого извлечения деталь будет возвращаться обратно. Но если после извлечения детали она не будет возвращена обратно, то извлечение второй раз бракованной детали будет зависимым событием, так как вероятность изменяется от того, вынута первая деталь бракованной или годной.
Если события A и B зависимы, то вероятность появления события B, вычисленная в предположении, что событие A наступило, называется условной вероятностью события B обозначается символом P(B/A)[1].
Пример 4. В урне 4 белых шара и 6 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие B), если при первого испытании был извлечен черный шар (событие A).
Решение. После первого испытания в урне осталось9 шаров, из них 4 белых. Искомая условная вероятность
P(B/A) = 4/9.
Для зависимых событий правило умножения вероятностей может быть сформулировано следующим образом: вероятность появления нескольких зависимых событий A, В и C одновременно равна произведению их вероятностей, вычисленных для каждого из них в предположении, что предшествующие ему события имели место, т. е.
Р(А и В и С) = Р(А)×Р(В/А)×Р(С/АВ).
Пример 5. В ящике находится 100 деталей, из них 10 бракованных. Определить вероятность извлечения подряд трех бракованных деталей, если после извлечения каждой детали они обратно в ящик не возвращаются.
Решение. Вероятность того, что первая извлеченная деталь окажется бракованной (событие A)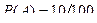 
.
Вероятность того, что вторая извлеченная деталь окажется также бракованной (событие B) при условии, что первая была бракованной, т. е. условная вероятность
.
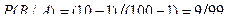Вероятность того, что и третья извлеченная деталь окажется снова бракованной (событие C) при условии, что первые две были бракованными, т. е. условная вероятность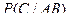 
составит
.
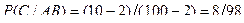По правилу умножения, искомая вероятность
.
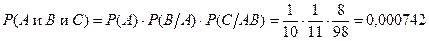Для независимых событий правило умножения вероятностей является следствием предыдущего правила. Для независимых событий условная вероятность равна безусловной вероятности: т. е. P(B / A) = P(B), поэтому вероятность появления нескольких независимых событий равна произведению их вероятностей:
P(A и B и C) = P(A)×P(B)×P(C).
Пример 6. По условиям предыдущего примера определить вероятность извлечения подряд трех бракованных деталей, если после каждого извлечения деталь возвращается обратно в ящик.
Решение.
.
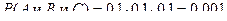Замечание. При вычислении вероятностей часто используют формулы комбинаторики, в частности, при определении количества возможных исходов испытаний или числа исходов, благоприятствующих рассматриваемому событию. Приведем наиболее употребительные формулы комбинаторики [1].
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.
Число всех возможных перестановок
,
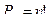где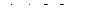 
.
Пример 7. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в отображение числа только один раз?
Решение. Искомое число трехзначных чисел
.
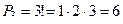Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком расположения. Число их возможных размещений
.
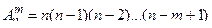Пример 8. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
Решение. Искомое число сигналов
.
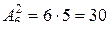Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число их возможных сочетаний
.
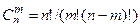Пример 9. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Решение. Искомое число способов
.
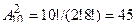Заметим, выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, например, среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т. д., то число перестановок с повторениями определяют по формуле
,
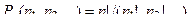где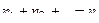 
.
При решении задач комбинаторики используют следующие правила.
Правило суммы. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может быть выбран n способами, то выбрать либо A , либо B можно m+n способами.
Правило произведения. Если объект A может быть выбран из совокупности m способами и после каждого такого выбора объект B можно выбрать n способами, то пара объектов (A, B) в указанном порядке может быть выбрана mn способами.
Закон больших чисел
Из статистического определения вероятности можно сделать вывод, что между вероятностью и частостью какого-либо события существует приближенное равенство
,
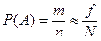которое будет тем точнее, чем больше число испытаний. Это положение было теоретически доказано Я. Бернулли и составляет содержание теоремы, носящей его имя.
Теорема Я. Бернулли гласит, что с вероятностью, как угодно близкой к достоверности, можно утверждать, что при достаточно большом числе испытаний N частость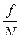 
появления события А, имеющего во всех испытаниях постоянную вероятность р, будет как угодно мало отличаться от этой вероятности, т. е.
,
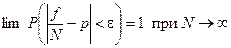где ε — как угодно малое положительное число.
Теорема Я- Бернулли вытекает непосредственно из теоремы П. Л. Чебышева, в которой доказывается, что среднее арифметическое значение независимых случайных величин Х1, Х2,..., Хп с увеличением числа наблюдений п приближается к их математическому ожиданию и тем точнее, чем больше п.
Теоремы П.Л. Чебышева, Я. Бернулли и некоторые другие, которые здесь не рассматриваются, получили общее название закона больших чисел. Этот закон имеет большое практическое значение. Например, на его основе, пользуясь приближенным равенством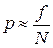 
, можно определить вероятность р какого-либо события по эмпирической частости и, наоборот, по известной вероятности можно определить ожидаемую частость этого события при N испытаниях, когда они еще не произведены. Закон больших чисел играет важную роль в статистических исследованиях и составляет основу применения статистических методов к изучению закономерностей массовых явлений.
Дата: 2019-02-25, просмотров: 206.
