Положение точки М по отношению к осям Оху (рис. 11.4) определится радиусом вектора:
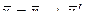 , где
, где  .
.
Дифференцируя дважды уравнение по времени, получим:
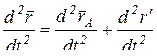 , отсюда следует, что
, отсюда следует, что
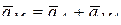 , (11.1)
, (11.1)
где 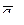 – ускорение точки А (полюс);
– ускорение точки А (полюс);
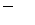 – ускорение точки при вращении вокруг точки А.
– ускорение точки при вращении вокруг точки А.
Так как точка М вращается вокруг полюса А по окружности, то разложим на составляющие – нормальную 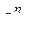 и касательную
и касательную 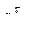 (рис. 11.1):
(рис. 11.1):
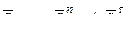
Тогда с учетом (11.1), получим (рис. 11.1а):
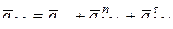 .
.

Рис. 11.1
Если полюс А движется не прямолинейно, то его ускорение будет слагаться из касательного и нормального и тогда
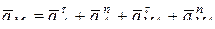 , (11.2)
, (11.2)
Пример 1 (18.11).
Для механизма, представленного на рис. 5.2 угловое ускорение кривошипа ОА 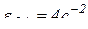 , ОА = 15см. Определить ускорение звена АВ
, ОА = 15см. Определить ускорение звена АВ  в данном положении механизма, при t = 1c.
в данном положении механизма, при t = 1c.
Решение

Рис. 11.2
Вначале определим ускорение точки В, выбрав за полюс точку А:
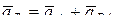 . (1)
. (1)
Так как точка А совершает вращательное движение по окружности вокруг неподвижного центра О, тогда:
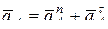 ,
,
где 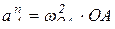 ;
;  – угловая скорость кривошипа ОА.
– угловая скорость кривошипа ОА.
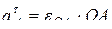 .
.
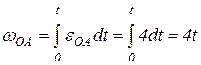 ;
;  , тогда:
, тогда: 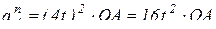 ;
;
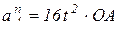 .
.
Точка В совершает вращательное движение вокруг точки А по окружности, тогда
 ,
,
где 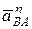 – нормальная составляющая ускорения точки В при вращении вокруг полюса А;
– нормальная составляющая ускорения точки В при вращении вокруг полюса А;
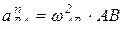 ;
;
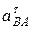 – касательная составляющая ускорения точки В при вращении вокруг полюса А;
– касательная составляющая ускорения точки В при вращении вокруг полюса А;
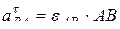 .
.
Для определения  и
и  определим скорость в точке В. Построим мгновенный центр скоростей для звена АВ. Точка О является м.ц.с. для звена АВ. Тогда
определим скорость в точке В. Построим мгновенный центр скоростей для звена АВ. Точка О является м.ц.с. для звена АВ. Тогда
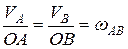 .
.
Так как 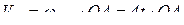 , тогда
, тогда
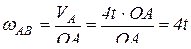 , отсюда
, отсюда 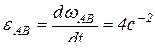 .
.
Изобразим отдельно звено АВ с соответствующими ускорениями (рис. 11.3):

Рис. 11.3
С учетом сделанных расчетов уравнение (1) запишем в виде:
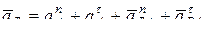 .
.
Спроектируем это векторное уравнение ВА на оси координат:
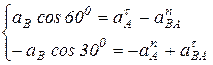 .
.
Подставляя полученные значения, получим:
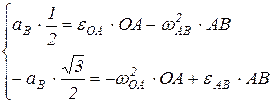 .
.
Из треугольника ОАВ сторона 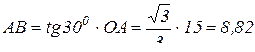 см.
см.
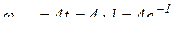 ;
; 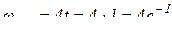 .
.
Тогда 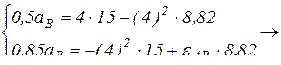
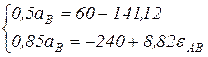
Полученная система двух уравнений имеет две неизвестные: 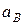 и
и  . Решая эту систему относительно неизвестных, получим:
. Решая эту систему относительно неизвестных, получим: 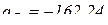 см/с2, знак минус (-) означает, что истинное направление ускорения точки имеет противоположное направление выбранному;
см/с2, знак минус (-) означает, что истинное направление ускорения точки имеет противоположное направление выбранному; 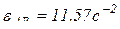 – угловое ускорение звена АВ.
– угловое ускорение звена АВ.
Так как точки D и В принадлежат одному звену DB, которое совершает возвратно-поступательное движение, поэтому все точки этого звена имеют одинаковые скорости и ускорения по величине и направлению. Вследствие этого ускорение точки D будет: 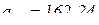 см/с2 и направлено вертикально вверх.
см/с2 и направлено вертикально вверх.
Ответ: 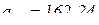 см/с2,
см/с2, 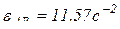 .
.
Пример 2.
На рис. 11.4. представлен механизм в данном положении: 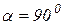 ,
, 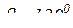 ,
, 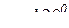 ,
, 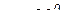 ,
,  , I1 = 0,6м, I2 = 1,2м, I3 = 1,4м, I4 = 0,8м,
, I1 = 0,6м, I2 = 1,2м, I3 = 1,4м, I4 = 0,8м, 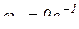 . Определить VA, VB, VD, VE,
. Определить VA, VB, VD, VE, 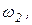
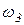 ,
, 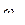 , аА, аВ, а D, аЕ,
, аА, аВ, а D, аЕ,  ,
,  ,
,  ,
,  . Точка D является серединой звена I2.
. Точка D является серединой звена I2.

Рис. 11.4
Решение
Определим скорость точки А. Так как точка А движется по окружности, то
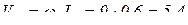 м/с.
м/с.
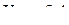 м/с.
м/с.
Вектор скорости 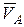 перпендикулярен I1.
перпендикулярен I1.
Вектор скорости точки В направлен перпендикулярно звену I4, а для вычисления модуля, определим мгновенный центр скоростей звена I2, которому принадлежат точки А, В и C2 – является мгновенным центром скоростей звена I2. Составим соотношение:
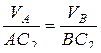 , отсюда
, отсюда 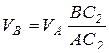 .
.
Так как угол С2ВА = 600, угол ВАС2 = 180-120 = 600, то угол ВС2А = 600.
Это означает, что треугольник ВС2А является равносторонним поэтому
ВС2 =АС2, тогда VB = VA = 5,4 м/с., т.е. VB = 5,4 м/с.
Для определения скорости точки D соединим точку С2 с точкой D и проведем линию, перпендикулярную DC2. Так как в равнобедренном треугольнике медиана является высотой и биссектрисой, то направление вектора скорости точки D совпадет с направлением звена I2. Модуль скорости точки D определим из соотношения:
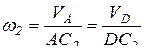 , отсюда
, отсюда 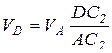 .
.
Из прямоугольного треугольника DC2A следует, что
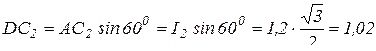 (м)
(м)
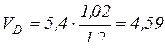 (м/с);
(м/с); 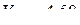 м/с.
м/с.
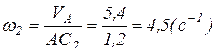 ;
; 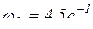 .
.
Направление скорости точки Е совпадает с направляющей ползуна, т.е. имеет вертикальное направление. Зная направления векторов скоростей точек D и Е, принадлежащих звену I3, определим мгновенный центр скоростей звена I3. Это будет точка С3, тогда составим соотношение:
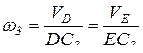 , отсюда
, отсюда 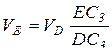 .
.
Рассмотрим треугольник С3DE. Так как угол С3 = 300 и угол Е = 300, то этот треугольник равнобедренный, т.е. DE = DC3;
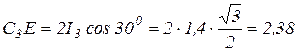 (м);
(м);
Тогда 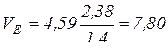 (м/с);
(м/с); 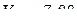 м/с.
м/с.
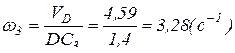 ;
; 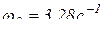 .
.
Определим угловую скорость звена I4:
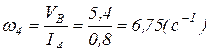 ;
; 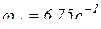 .
.
Определим ускорение точки А (рис. 11.5).

Рис. 11.5
Точка А совершает вращательное движение по окружности вокруг неподвижного центра О1. Поэтому ускорение точки А разложим на нормальную и касательную составляющие:
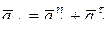 ,
,
где 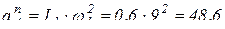 (м/с2);
(м/с2); 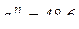 м/с2.
м/с2.
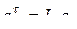 , так как по условию задачи
, так как по условию задачи 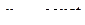 , а
, а 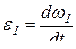 , то
, то 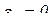 , тогда
, тогда 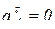 . Поэтому
. Поэтому 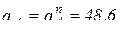 м/с2;
м/с2; 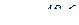 м/с2.
м/с2.
Определим ускорение точки В, выбрав точку А за полюс. Тогда
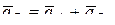 , (1)
, (1)
где 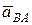 – ускорение, связанное с вращением точки В вокруг А.
– ускорение, связанное с вращением точки В вокруг А.
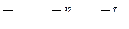 , (2)
, (2)
Подставляя (2) в (1), получим:
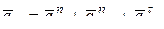 . (3)
. (3)
Так как точка В вращается вокруг неподвижного центра О2, то разложим ускорение точки В на нормальную и касательную составляющие:
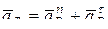 . (4)
. (4)
Подставляя уравнение (4) в уравнение (3), получим:
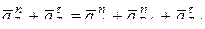 . (5)
. (5)
Выберем оси координат таким образом, что ось х будет направлена вдоль звена I2.
Спроектируем уравнение (5) на оси координат:
| на ось х: |
| на ось у: |
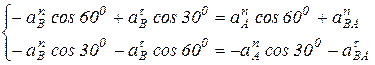 (6)
(6)
Так как:  (м/с2);
(м/с2); 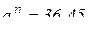 м/с2.
м/с2.
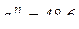 м/с2.
м/с2.
 (м/с2);
(м/с2); 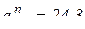 м/с2.
м/с2.
В системе двух уравнений (6) имеется две неизвестные: 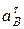 и
и 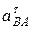 , т.е. система уравнений имеет решение и притом только единственное. Подставим численные значения в систему уравнений (6):
, т.е. система уравнений имеет решение и притом только единственное. Подставим численные значения в систему уравнений (6):
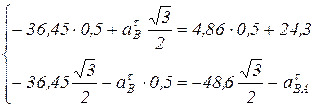
Решая это уравнение, получим:
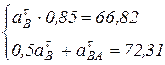 , отсюда следует, что
, отсюда следует, что 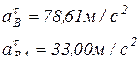
В связи с тем, что 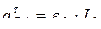 ,
,
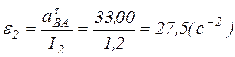 ;
; 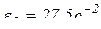 .
.
Ускорение точки В будет:
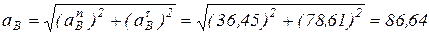 (м/с2);
(м/с2);
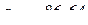 м/с2.
м/с2.
Определим ускорение точки D, выбрав за полюс точку А. Тогда
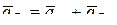 , (7)
, (7)
Так как  , а ускорение
, а ускорение 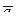 разложим на составляющие
разложим на составляющие 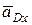 и
и 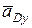 (рис. 11.6).
(рис. 11.6).

Рис. 11.6
Учитывая, что 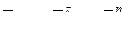 , уравнение (7) примет вид:
, уравнение (7) примет вид:
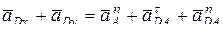 . (8)
. (8)
Спроектируем векторное уравнение (8) на выбранные оси координат:
на ось х: 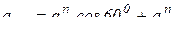
на ось у: 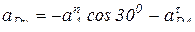 .
.
Полученная система двух уравнений имеет две неизвестные: 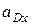 и
и 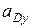 , так как
, так как 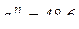 м/с2;
м/с2; 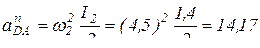 (м/с2);
(м/с2); 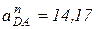 м/с2;
м/с2; 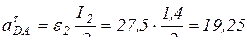 (м/с2);
(м/с2); 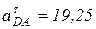 м/с2. Тогда полученная система двух уравнений примет вид:
м/с2. Тогда полученная система двух уравнений примет вид:
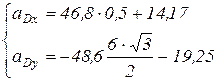
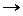
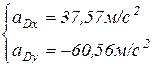
Отрицательное значение 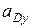 указывает, что истинное направление вектора противоположно выбранному.
указывает, что истинное направление вектора противоположно выбранному.
Ускорение точки D будет:
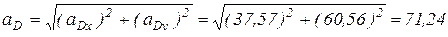 (м/с2);
(м/с2);
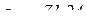 м/с2.
м/с2.
Определим ускорение точки Е. Направление вектора ускорения точки Е, будет совпадать с направляющей ползуна (рис. 11.7). На рис. 11.7 изображен фрагмент механизма, включающий звено I3 и ползун Е.

Рис. 11.7
Ускорение точки Е будем определять, выбрав за полюс точку D, тогда:
 , (9)
, (9)
Учитывая, что 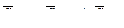 , и
, и 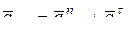 , тогда уравнение (9) примет вид:
, тогда уравнение (9) примет вид:
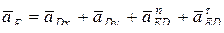 , (10)
, (10)
Выберем оси координат, как показано на рис. 11.7, т.е. ось х направим вдоль направления звена I3 и спроектируем векторное уравнение (10) на оси координат:
на ось х: 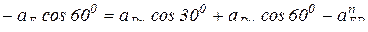
на ось у: 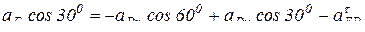 .
.
Представленные два уравнения образуют систему двух уравнений с двумя неизвестными: 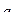 и
и 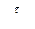 , так как
, так как 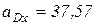 м/с2;
м/с2; 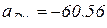 м/с2;
м/с2;  (м/с2), т.е.
(м/с2), т.е. 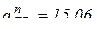 м/с2. Подставляя численные значения, получим систему двух уравнений с двумя неизвестными:
м/с2. Подставляя численные значения, получим систему двух уравнений с двумя неизвестными:
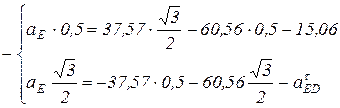
После преобразований получим:
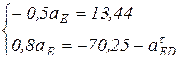 отсюда следует
отсюда следует 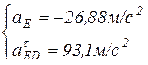
Ускорение точки Е составляет 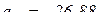 м/с2 (знак минус указывает, что истинное направление вектора ускорения имеет противоположное значение выбранному).
м/с2 (знак минус указывает, что истинное направление вектора ускорения имеет противоположное значение выбранному).
Так как 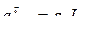 , то
, то 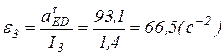 , т.е.
, т.е. 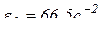 .
.
Таким образом, определены все значения кинематических характеристик, указанные в вопросе задачи.
Вопросы для самоконтроля
1. Определение ускорений точек твердого тела?
2. Определение углового ускорения твердого тела при плоском движении?
Задачи, рекомендуемые для самостоятельного решения: 18.1 – 18.36 [2].
Литература: [1], [3], [4].
 Лекция 12
Лекция 12
Сложное движение точки
Если точка движется одновременно по отношению к двум системам отсчета, из которых одна считается условно неподвижной, а другая движется по отношению к первой, то движение, совершаемое при этом точкой, называется составным или сложным.
Например, человек перемещается по вагону поезда (подвижная система отсчета), который движется по отношению к Земле (неподвижная система отсчета).
Рассмотрим сложное движение точки М, перемещающейся по отношению к подвижной системе отсчета ОXYZ, которая в свою очередь как-то движется относительно другой системы отсчета O1X1Y1Z1 условно названной неподвижной (рис. 12.1).
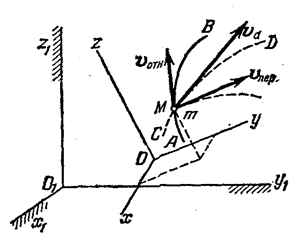
Рис. 12.1
Движение, совершаемое точкой М по отношению к подвижным осям координат, называется относительным движением. Траектория АВ описываемая в относительном движении называется относительной траекторией. Скорость движения точки М по отношению к осям OXYZ называется относительной скоростью (обозначается 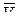 ), а ускорение точки в этом движении – относительным ускорением (обозначается
), а ускорение точки в этом движении – относительным ускорением (обозначается 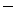 ). При вычислении
). При вычислении 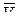 и
и 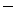 оси OXYZ можно считать неподвижными.
оси OXYZ можно считать неподвижными.
Движение, совершаемое подвижной системой отсчета OXYZ и всеми неизменно связанными с ней точками пространства по отношению к неподвижной системе O1X1Y1Z1 является для точки М переносным движением.
Скорость неизменно связанной с подвижными осями OXYZ точки m, с которой в данный момент совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент времени (обозначается 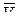 ), а ускорение этой точки – переносным ускорением точки М (обозначается
), а ускорение этой точки – переносным ускорением точки М (обозначается 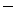 ).
).
На рис. 12.1 АВ – траектория точки М в относительном движении и 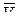 к ней касательная в этой точке. Поскольку подвижная система координат OXYZ перемещается со скоростью
к ней касательная в этой точке. Поскольку подвижная система координат OXYZ перемещается со скоростью 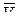 , то результирующей скоростью будет
, то результирующей скоростью будет 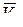 , называемая абсолютной скоростью, которая является касательной к траектории CD, которая называется абсолютной траекторией. Движение точки М по абсолютной траектории – есть абсолютное движение, а ускорение – абсолютным ускорением.
, называемая абсолютной скоростью, которая является касательной к траектории CD, которая называется абсолютной траекторией. Движение точки М по абсолютной траектории – есть абсолютное движение, а ускорение – абсолютным ускорением.
Сложение скоростей
Теорема. При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:
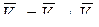 , (12.1)
, (12.1)

Рис. 12.2
На рис. 12.2: АВ – траектория точки М в относительном движении;
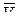 – относительная скорость точки М;
– относительная скорость точки М;
А1В1– положение траектории точки М вследствие переносного движения.
Если угол между 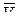 и
и 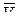 составляет α, то формула (12.1) в скалярном виде будет:
составляет α, то формула (12.1) в скалярном виде будет:
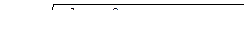 , (12.2)
, (12.2)
Сложение ускорений
Теорема Кориолиса. Абсолютное ускорение точки равно геометрической сумме трех ускорений: относительного, характеризующего изменение относительной скорости в относительном движении; переносного, характеризующего изменение скорости в переносном движении и кориолисово, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости в относительном движении.
 , (12.3)
, (12.3)
где 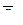 – кориолисово ускорение.
– кориолисово ускорение.
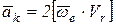 . (12.4)
. (12.4)
Кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки. Если угол между векторами 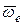 и
и 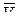 составляет угол α, то модуль кориолисова ускорения будет равен:
составляет угол α, то модуль кориолисова ускорения будет равен:
 . (12.5)
. (12.5)
Частные случаи. Кориолисово ускорение будет равно нулю в следующих случаях:
1. Когда 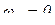 , т.е. переносное движение является поступательным, или, если угловая скорость равна нулю;
, т.е. переносное движение является поступательным, или, если угловая скорость равна нулю;
2. Когда 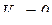 , т.е. когда относительная скорость равна нулю;
, т.е. когда относительная скорость равна нулю;
3. Когда 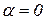 и
и  , т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или, если в данный момент времени вектор
, т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или, если в данный момент времени вектор 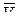 параллелен этой оси.
параллелен этой оси.
Определение направления кориолисова ускорения (правило Жуковского Е.Н.):
Для определения направления кориолисова ускорения необходимо выполнить следующее:
5. провести плоскость, перпендикулярную вектору угловой скорости;
6. спроектировать на эту плоскость вектор скорости в относительном движении;
7. повернуть проекцию вектора скорости на 900 по ходу вращения переносного движения.
Пример 1.
Точка М в относительном движении из положения 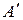 движется по диагонали квадрата BCDA по закону
движется по диагонали квадрата BCDA по закону 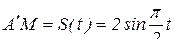 , см. Квадрат BCDA вращается вокруг неподвижной оси по закону
, см. Квадрат BCDA вращается вокруг неподвижной оси по закону 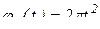 , рад. Сторона квадрата CD = 4см. Определить абсолютную скорость и абсолютное ускорение при t = 1c.
, рад. Сторона квадрата CD = 4см. Определить абсолютную скорость и абсолютное ускорение при t = 1c.
Решение
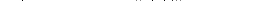
Рис. 12.3
Определим абсолютную скорость точки М в момент времени t = 1c. Точка М перемещается по диагонали прямоугольника из положения 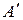 . Так как относительное движение прямолинейное, то скорость точки М в относительном движении будет:
. Так как относительное движение прямолинейное, то скорость точки М в относительном движении будет:
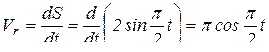 .
.
При t = 1c 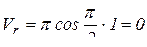 (м/с);
(м/с); 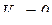 м/с.
м/с.
Вращательное движение точки М вокруг оси ОО1 является переносным движением. Траектория переносного движения является окружность с радиусом r. Определим положение точки М на прямой АВ при t = 1c.
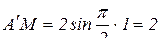 (см);
(см); 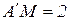 см.
см.
Из треугольника MDK следует, что 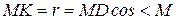
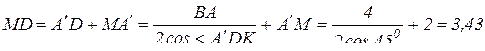 (см);
(см);
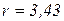 см.
см.
Так как точка М совершает в переносном движении вращение по окружности с радиусом r, то скорость в переносном движении будет:
 ,
,
где 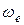 – угловая скорость переносного движения.
– угловая скорость переносного движения.
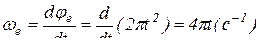 ;
;
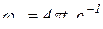 .
.
Тогда
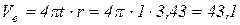 (см/с);
(см/с);
 см/с.
см/с.
Вектор скорости 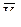 направлен по касательной к траектории в точке М, т.е. перпендикулярно плоскости чертежа.
направлен по касательной к траектории в точке М, т.е. перпендикулярно плоскости чертежа.
Так как при сложном движении точки:
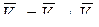 ,
,
то вследствие того, что 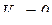
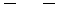 , тогда
, тогда  см/с.
см/с.
Абсолютная скорость точки М при t = 1c по модулю равна 43,1 см/с и направлена перпендикулярно плоскости чертежа (на нас).
Определим абсолютное ускорение точки М согласно теоремы сложения ускорений:
 .
.
Так как в относительном движении точка движется по прямой, то:
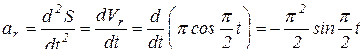 .
.
При t = 1c, 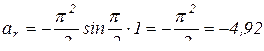 (см/с2);
(см/с2);
 см/с2.
см/с2.
Вследствие движения точки М в переносном движении по окружности (рис. 12.4а):
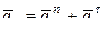 ,
,
где 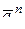 – нормальная составляющая ускорения в переносном движении.
– нормальная составляющая ускорения в переносном движении.
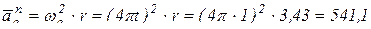 (см/с2);
(см/с2);
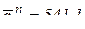 см/с2., вектор нормальной составляющей ускорения направлен по радиусу к оси вращения.
см/с2., вектор нормальной составляющей ускорения направлен по радиусу к оси вращения.
 ;
;
 – угловое ускорение в переносном движении;
– угловое ускорение в переносном движении;
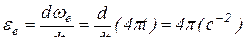 ;
; 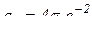 .
.
Тогда 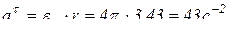 ;
; 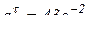 .
.
Вектор касательной составляющей ускорения направлен в сторону направления вектора скорости (так как движение ускоренное, вследствие того, что 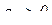 ), т.е. перпендикулярно плоскости чертежа (на нас).
), т.е. перпендикулярно плоскости чертежа (на нас).

а) б)
Рис. 12.4
Определим кориолисово ускорение:
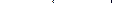
или в скалярной форме:
 ,
,
где 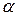 – угол между векторами
– угол между векторами 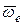 и
и 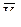 .
.
Так как 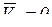 , то и кориолисово ускорение равно нулю, т.е.:
, то и кориолисово ускорение равно нулю, т.е.:
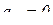 см/с2.
см/с2.
В результате проведенных вычислений установлено, что на точку М в момент времени t = 1c действует три составляющих ускорения: 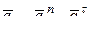 (рис. 12.4б). Векторы
(рис. 12.4б). Векторы  лежат в плоскости чертежа и угол между ними составляет 450, тогда модуль суммы этих двух векторов будет:
лежат в плоскости чертежа и угол между ними составляет 450, тогда модуль суммы этих двух векторов будет:
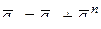 ,
,
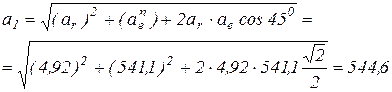 (см/с2);
(см/с2);
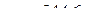 см/с2.
см/с2.
Вектор 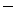 находится в плоскости чертежа, а вектор
находится в плоскости чертежа, а вектор 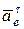 – перпендикулярен плоскости чертежа, тогда результирующий вектор – вектор абсолютного ускорения будет:
– перпендикулярен плоскости чертежа, тогда результирующий вектор – вектор абсолютного ускорения будет:
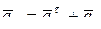
или в скалярной форме:
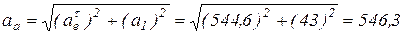 (см/с2);
(см/с2);
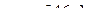 см/с2.
см/с2.
Ответ:  см/с,
см/с, 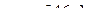 см/с2.
см/с2.
Пример 2.
Точка М перемещается по окружности диска радиусом R = 2 см по закону 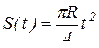 из положения А. Диск вращается вокруг неподвижной оси по закону
из положения А. Диск вращается вокруг неподвижной оси по закону 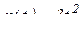 . Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1c.
. Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1c.
Решение

Рис. 12.5
R = 2см;
l = 5см.
Анализ характера движения точки М (рис. 12.5) свидетельствует, что движение по окружности диска радиусом R является относительным, а движение диска вокруг неподвижной оси – переносное движение.
Определим положение точки М на окружности диска в момент t = 1c:
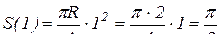 (см).
(см).
Длина дуги, пройденная точкой М за 1с, составляет 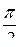 см. Определим длину дуги в радианах:
см. Определим длину дуги в радианах:
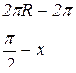
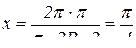 (рад.)
(рад.)
Отсюда следует, что дуга, пройденная точкой М за 1с, составляет 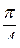 рад., или 900 (положение М). Направление вектора скорости
рад., или 900 (положение М). Направление вектора скорости  будет направлено по касательной к окружности в этой точке (рис. 12.5).
будет направлено по касательной к окружности в этой точке (рис. 12.5).
Определим абсолютную скорость точки М в момент t = 1c. По правилу сложения скоростей:
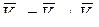 .
.
Модуль скорости в относительном движении будет:
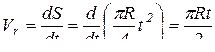 ; при t = 1c.
; при t = 1c.
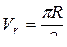 (см/с)
(см/с) 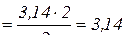 см/с.
см/с.
В переносном движении точка М совершает вращательное движение по окружности с радиусом  вокруг неподвижной оси (рис. 12.6а).
вокруг неподвижной оси (рис. 12.6а).

а) б) в)
Рис. 12.6
Направление вектора переносной скорости 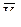 перпендикулярно плоскости чертежа в сторону «от нас».
перпендикулярно плоскости чертежа в сторону «от нас».
Модуль скорости 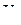 определим:
определим:
 ,
,
где 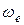 – угловая скорость вращения диска вокруг оси.
– угловая скорость вращения диска вокруг оси.
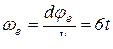 ; при t = 1c
; при t = 1c 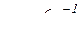 .
.
Тогда
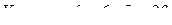 (см/с);
(см/с);
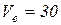 см/с.
см/с.
Векторы скоростей 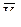 и
и 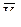 ортогональны, так как расположены в двух взаимно пересекающихся плоскостях. Поэтому модуль результирующего вектора
ортогональны, так как расположены в двух взаимно пересекающихся плоскостях. Поэтому модуль результирующего вектора 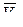 определим:
определим:
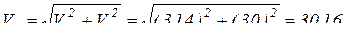 (см/с);
(см/с);
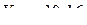 см/с.
см/с.
Определим абсолютное ускорение точки М в момент времени t = 1c. Согласно правилу сложения ускорений:
 .
.
В относительном движении ускорение точки М разложим на две составляющие 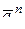 и
и 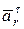 , так точка движется по окружности (рис. 12.6б):
, так точка движется по окружности (рис. 12.6б):
 ,
,
где 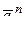 – нормальная составляющая вектора ускорения точки М в относительном движении.
– нормальная составляющая вектора ускорения точки М в относительном движении.
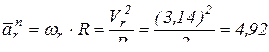 (см/с);
(см/с); 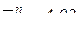 см/с.
см/с.
Вектор 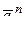 направлен по радиусу к центру окружности О.
направлен по радиусу к центру окружности О.
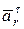 – касательная составляющая вектора ускорения точки М в переносном движении.
– касательная составляющая вектора ускорения точки М в переносном движении.
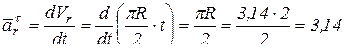 (см/с2);
(см/с2); 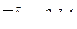 см/с2.
см/с2.
Вектор 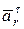 направлен по касательной и окружности и совпадает с направлением вектора скорости, так как движение ускоренное.
направлен по касательной и окружности и совпадает с направлением вектора скорости, так как движение ускоренное.
Так как в переносном движении точка М движется по окружности вокруг неподвижной оси, то ускорение разложим на составляющие (рис. 12.6а):
 ,
,
где 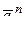 – нормальная составляющая вектора ускорения в переносном движении.
– нормальная составляющая вектора ускорения в переносном движении.
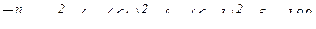 (см/с2);
(см/с2); 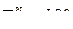 см/с2.
см/с2.
Вектор 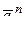 направлен к неподвижной оси.
направлен к неподвижной оси.
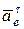 – касательная составляющая вектора ускорения в переносном движении.
– касательная составляющая вектора ускорения в переносном движении.
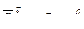 ;
;
 – угловое ускорение диска в переносном движении:
– угловое ускорение диска в переносном движении:
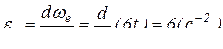 ;
; 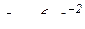 .
.
 (см/с2);
(см/с2); 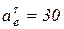 см/с2.
см/с2.
Вектор 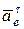 направлен перпендикулярно плоскости чертежа и совпадает с направлением вектора скорости переносного движения (так как движение ускоренное).
направлен перпендикулярно плоскости чертежа и совпадает с направлением вектора скорости переносного движения (так как движение ускоренное).
Определим кориолисово ускорение:
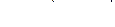 .
.
Модуль кориолисова ускорения равен:
 ,
,
где 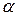 – угол между векторами
– угол между векторами 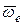 и
и 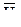 .
.
Согласно «правила буравчика» в данном случае вектор угловой скорости переносного движения направлен параллельно неподвижной оси, вокруг которой вращается диск. Тогда расположение векторов 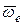 и
и 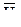 будет таким, как представлено на рис. 12.6в. В этом случае вектор кориолисова ускорения, согласно правила Жуковского, будет направлен перпендикулярно плоскости чертежа «на нас».
будет таким, как представлено на рис. 12.6в. В этом случае вектор кориолисова ускорения, согласно правила Жуковского, будет направлен перпендикулярно плоскости чертежа «на нас».
Модуль  будет равен:
будет равен:
 (см/с2);
(см/с2);
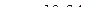 см/с2.
см/с2.
Таким образом, на точку М действуют пять составляющих ускорений (рис. 12.7).

Рис. 12.7
Векторы 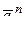 и
и 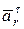 лежат вдоль одной прямой в одну сторону, поэтому сумма этих векторов будет:
лежат вдоль одной прямой в одну сторону, поэтому сумма этих векторов будет:
 ,
,
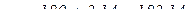 (см/с2).
(см/с2).
Векторы  и
и 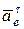 направлены вдоль одной прямой, но в противоположные стороны, тогда результирующий вектор
направлены вдоль одной прямой, но в противоположные стороны, тогда результирующий вектор 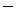 будет:
будет:
 ,
,
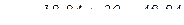 (см/с2).
(см/с2).
Получившаяся система векторов 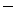 ,
, 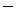 и
и 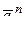 образуют ортогональную систему, т.е. взаимноперпендикулярны, поэтому результирующий вектор
образуют ортогональную систему, т.е. взаимноперпендикулярны, поэтому результирующий вектор 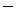 можно представить:
можно представить:
 ,
,
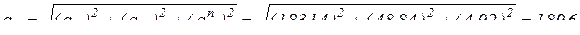 (см/с2)
(см/с2)
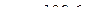 см/с2.
см/с2.
Ответ: 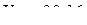 см/с,
см/с, 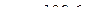 см/с2.
см/с2.
Вопросы для самоконтроля
1. Что такое сложное движение точки?
2. Что такое относительное движение? Его кинематические характеристики?
3. Что такое переносное движение? Его кинематические характеристики?
4. Что такое абсолютное движение? Его кинематические характеристики?
5. Как определяется абсолютная скорость точки?
6. Теорема Кориолиса?
7. Как определяется величина и направление кориолисова ускорения?
Задачи, рекомендуемые для самостоятельного решения: 22.1 – 22.24, 23.1 – 23.66 [2].
Литература: [1], [3], [4].
Приложения
Приложение 1
Дата: 2019-02-25, просмотров: 503.