Если поверхность считается шероховатой, то надо учитывать силу трения. Т.е. шероховатая связь будет слагаться из двух составляющих: из нормальной реакции 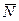 и перпендикулярной к ней силы трения 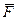. Поэтому полная реакция  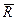будет отклонена от нормали и поверхности на некоторый угол (рис. 6.1).

Рис. 6.1

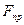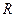При изменении силы трения от нуля до  сила  будет меняться от  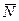до 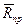, а ее угол с нормалью будет расти от нуля до некоторого предельного значения 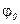. Наибольший угол 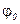, который образует полная реакция шероховатой связи с нормалью с поверхностью называется углом трения. Из чертежа видно, что

.

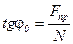Так как 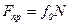, то отсюда находим следующую связь между углом трения и коэффициентом трения

.

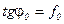Трение качения и верчения

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

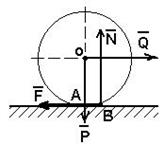
Рассмотрим круглый цилиндрический каток, лежащий на горизонтальной шероховатой поверхности (плоскости), вследствие деформации катка касания тел происходит вдоль некоторой площадки АВ (рис. 6.2).

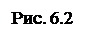Пусть Р – сила тяжести катка, радиусом R, к которому приложена сила Q. Под действием силы Q давление на поверхность возрастает от края А к краю В, поэтому сила реакции N смещена относительно центра катка О. Величина смещения (расстояние АВ) возрастает с увеличением силы Q до некоторой предельной величины К. Поэтому в предельном положении на каток будет действовать пара (Q_пр, F) с моментом Q_пр*R и уравновешивающая ее пара (N, P) с моментом N_к. Из равенства моментов определяем Q_пр*R = Nk или Q_пр = К*N/R.

При Q < Q_пр каток находится в покое; при Q > Q_пр  – начинается качение.

Величина К называется коэффициентом трения; К измеряется в линейных единицах, например, в сантиметрах.

Понятие о трении верчения

Если к шару, лежащему на горизонтальной плоскости приложить пару сил с моментом М, расположенную тоже в горизонтальной плоскости, то пара будет стремиться повернуть шар вокруг вертикальной оси. Опыт показывает, что шар начнет вращаться только тогда, когда значение М будет больше некоторой предельной величины М_пр, определяемой равенством

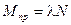,                                             (6.1)

где N – сила нормального давления на плоскость, равная в данном случае весу шара. Объясняется этот результат наличием трения верчения шара о плоскость. Входящий в равенство (6.1) коэффициент λ, имеющий размерность длины, называется коэффициентом трения верчения. По величине этот коэффициент меньше трения качения k.

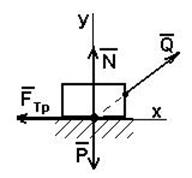
Пример. Определить, какую силу Q, направленную под углом a = 30⁰ к горизонту, надо приложить к грузу массой 10кг, лежащему на горизонтальной поверхности, чтобы его сдвинуть с места, если статический коэффициент трения груза о плоскость ¦₀ = 0,8 (рис. 6.3).

Решение : на данное тело действуют следующие силы:

P – сила тяжести = mg;

N – сила нормальной реакции опоры;

F_тр – сила трения;

Q – действующая сила.

При равновесии тела должно выполнятся условие: N + Q + P + F_тр = 0.

Выберем систему координат и спроектируем это векторное уравнение на оси Х и Y:

Q cosa - F_тр = 0; N + Q sina - P = 0;

Отсюда следует, что N = p – Q sina, так как F_тр = ¦₀N, то

Q cosa = ¦₀N = ¦₀P – Q*¦₀ sina или Q(cosa + ¦₀ sina) = ¦₀P, отсюда

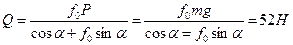
Ответ: Q = 52H.

Центр тяжести.

Центр параллельных сил

Рассмотрим систему параллельных и одинаково направленных сил F₁, F₂, …, F_n приложенных к телу в точках A₁, A₂, …, A_n. Эта система имеет равнодействующую R, направленную как слагаемые силы, а по модулю равна: R = å F_i.

Точка С, через которую проходит линия действия равнодействующей силы параллельных сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол, называется центром параллельных сил.

Формулы для определения координат центра параллельных сил:

; ; .

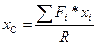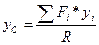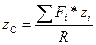Центр тяжести твердых тел

Твердое тело состоит из набора частиц, которые обладают силой тяжести. Силы тяжести всех этих частиц направлены к центру Земли, но, учитывая, что размеры Земли несоизмеримо больше размеров тела, то эти силы можно считать параллельными.

Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела при любом положении тела в пространстве.

Координаты центра тяжести тела как центра параллельных сил определяются по формулам:

; ; ,

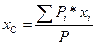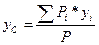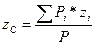где Pi – сила тяжести i-ой частицы тела;

   P – сила тяжести всего тела: P = å P_i.

Координаты центра тяжести однородного тела:

; ; ,

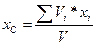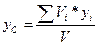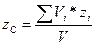где Vi – объем i-ой частицы тела;

   V – объем тела, V = å V_i.

Координаты центра тяжести однородной линии:

; ; ,

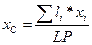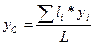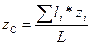где li – длина i-ой части линии;

   L – длина всей линии, L = å l_i.