Координаты однородной плоской фигуры определяются по формулам:
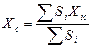, (6.2)
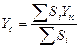, (6.3)
где Xic, Yic – координаты центра тяжести
i - части фигуры,
Si - площадь i – части фигуры.
Центры тяжести некоторых однородных тел:
1. Треугольник
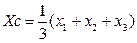, (6.4)
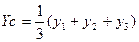, (6.5)
где x 1 , x 2 , x 3 , y 1 , y 2 , y 3 – соответственно абсциссы и ординаты вершин треугольника.
2. Круговой сектор (рис. 6.4):
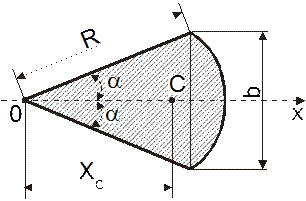
Рис. 6.4
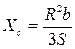(6.6)
Площадь сектора: S = a R 2 (6.7)
3. Круговой сегмент (рис. 6.5):
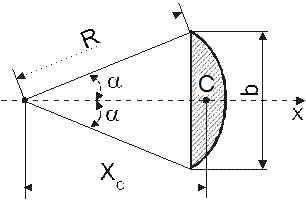
Рис. 6.5
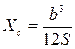, (6.8)
Площадь сегмента: S = ½ R 2 (2 a – sin 2 a ), (6.9)
Примеры выполнения заданий
Задача 1 (способ разбиения)
Определить координаты центра тяжести плоской фигуры, представленной на
рис. 6.6:
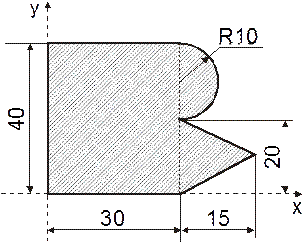
Рис. 6.6
Решение
Разбиваем данное плоское тело на части, для каждой из которых положение центра тяжести известно. Тогда координаты центра тяжести всего тела можно вычислить по формулам (1) и (2).
В данном случае тело разбиваем на прямоугольник ABCL, треугольник LFK и полукруг CDF (рис. 6.7):
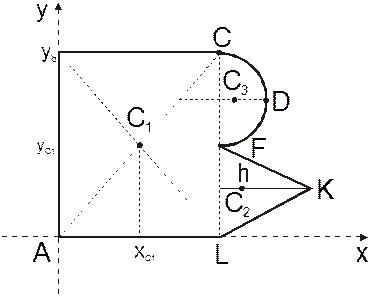
Рис. 6.7
Рассмотрим отдельно каждую часть фигуры:
Прямоугольник ABCL
Центр тяжести (С1) определяется на пересечении диагоналей АС и BL, т.е.
.
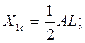
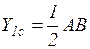Площадь определяется: S 1 = AL * AB
Подставляя численные значения, получим:
X1c = 15 мм; Y1c = 20 мм; S1 = 1200 мм 2 .
Треугольник LFK
Координаты центра тяжести (С2) определяются по формулам (3); (4).
Из рисунка видно, что координаты вершин являются:
L(30;0); F(30;20); K(45;10)
Площадь
,
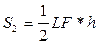где h – высота треугольника, опущенная из вершины К на сторону FL.
Подставляя численные значения, получим:
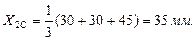
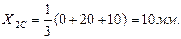
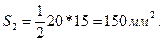
Полукруг CDF .
Координаты центра тяжести (С3) определяем по формуле (5).
Так как R = 10 мм; b = 20 мм;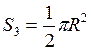 
, то, подставляя численные значения, получим:
X3C = 34 мм; Y3C = 30 мм; S3 = 157 мм2.
Для вычисления центра тяжести плоской фигуры составим таблицу:
| Номер элемента | Si мм2 | Xci, мм | Yci, мм | SiXci, мм3 | SiYci, мм3 |
| 1 | 1200 | 15 | 20 | 18000 | 24000 |
| 2 | 150 | 35 | 10 | 5250 | 1500 |
| 3 | 157 | 34 | 30 | 5350 | 4700 |
| 1507 | - | - | 28600 | 30200 |
В соответствии с формулами (1), (2) получим, что координаты центра тяжести всей фигуры будут:
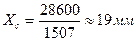
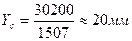
Ответ: координаты данной плоской фигуры: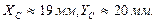 
Задача 2 (способ дополнения)
Определить площадь плоской фигуры, изображенной на рис. 6.8
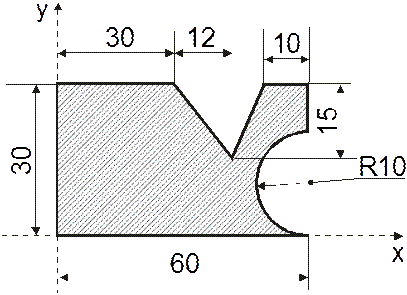
Рис. 6.8
Решение.
Разбиваем данное плоское тело на части согласно рисунку 6.9:
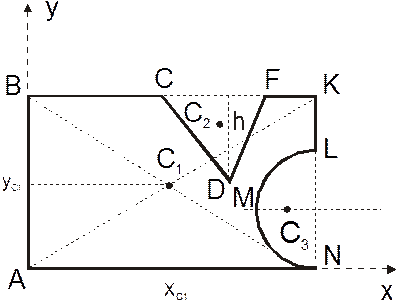
Рис. 6.9
| I часть II часть III часть | - - - | прямоугольник ABKN треугольник CDF полукруг LMN |
Причем площади дополняющих фигур треугольника CDF и полукруга LMN берутся с отрицательным знаком.
Рассмотрим отдельно каждую часть фигуры:
Прямоугольник ABKL
Центр тяжести (С1) определяется на пересечении диагоналей BN и AK,т.е.
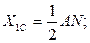
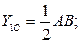
площадь определяется: S 1 = AN * BA
Подставляя численные значения, получим:
X1C = 30 мм.; Y1C = 15 мм.; S1 = 1800 мм2
Треугольник CDK
Координаты центра тяжести (С2) определяем по формулам (3), (4).
Из рисунка видно, что координаты вершин треугольника являются:
С(30;30); F(20;30); D(42;15)
Площадь
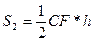
где h – высота треугольника, опущенная из вершины D на сторону CF.
Подставляя численные значения, получим:
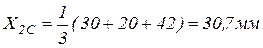
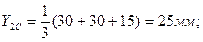
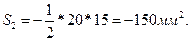
3. Полукруг MNL .
Координаты центра тяжести (С3) определяем по формуле (5).
Так как R = 10 мм; b = 20 мм;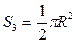 
, то, подставляя численные значения, получим:
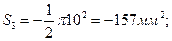
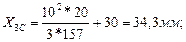
Y3C = 10 мм.
Для вычисления центра тяжести плоской фигуры составим таблицу:
| Номер элемента | Si Мм2 | Xci, мм | Yci, мм | SiXci, мм3 | SiYci, мм3 |
| 1 | 1800 | 30 | 15 | 54000 | 27000 |
| 2 | -150 | 30,7 | 25 | -4605 | -3750 |
| 3 | -157 | 34,3 | 10 | -5385,1 | -1570 |
| 1493 | - | - | 44009,9 | 21680 |
В соответствии с формулами (1), (2) получим, что координаты центра тяжести всей фигуры будут:
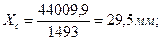
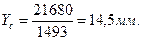
Ответ: координаты данной плоской фигуры: XC = 29,5 мм; YC = 14,5 мм.
Дата: 2019-02-25, просмотров: 447.
