Найти координаты центра тяжести плоской однородной фигуры (варианты 1-75).
Все размеры даны в миллиметрах.
Вопросы для самоконтроля
1. Что такое трение скольжения? Как определяется коэффициент трения скольжения?
2. Что такое трение качения и верчения? Как определяется коэффициенты трения качения и верчения?
3. Что такое центр тяжести тела?
4. Способы определения плоской фигуры?
Задачи, рекомендуемые для самостоятельного решения: 9.1 – 9.28 [2].
Литература: [1], [3], [4].
Кинематика
Лекция 7
Кинематика точки
Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Для определения положения движущегося тела (или точки) с тем телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, которая вместе с телом образует систему отсчета. Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к этой системе отсчета находится в покое. Если координаты каких-нибудь точек тела с течением времени изменяются, то тело по отношению к данной системе координат находится в движении.
Движение тел совершается в пространстве с течением времени. В механике рассматривается трехмерное евклидовое пространство. Время является скалярной величиной, непрерывно изменяющейся величиной. Отсчет времени ведется от некоторого начального (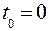 
), о выборе которого в каждом случае уславливаются. Разность между двумя последовательными моментами времени называется промежутком времени.
Кинематически задавать движение или закон движения тела (точки) – значит, задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.
Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие тела в целом, так и движение каждой из его точек в отдельности (траектории, скорости, ускорения и т.п.).
Вначале изучим движения точки, а затем перейдем к изучению кинематики твердого тела.
Способы задания движения точки.
Траектория
Чтобы задать движение точки, надо задать ее в любом положении по отношению к выбранной системе отсчета в любой момент времени. Для задания движения точки можно применять один из следующих трех способов:
1. Естественный;
2. Координатный;
3. Векторный.
Естественный способ задания движения
Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория – прямая линия, то движение точки называется прямолинейным; а если кривая – то движение точки называется криволинейным.
Пусть кривая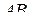 
является траекторией движения точки 
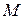относительно системы отсчета 
, 
, 
, 
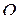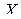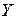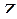, (рис. 1.1.).
Рис. 7.1.
Выберем на этой траектории какую-нибудь неподвижную точку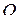 
, которую примем за начало отсчета; затем, рассматривая траекторию как криволинейную координатную ось, установим на ней положительное и отрицательное направление. Тогда положение точки 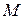будет однозначно определяться криволинейной координатой 
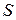, которая равна расстоянию от точки 
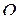до точки 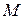. Чтобы знать положение точки 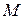на траектории, в любой момент времени надо знать зависимость:
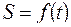(7.1.)
Уравнение (7.1.) выражает закон движения точки 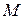вдоль траектории. Таким образом, чтобы задать движения точки естественным способом, надо знать:
1. Траекторию точки;
2. Начало отсчета на траектории;
3. Законы движения точки вдоль траектории в виде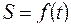 
.
Координатный способ задания движения
Положение точки по отношению к данной системе отсчета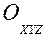 
, можно определить ее декартовыми координатами 
, 
, 
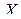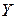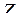(рис. 7.2.).
При движении все эти три координаты будут с течением времени изменяться. Чтобы знать закон движения точки, необходимо знать значения координаты точки для каждого момента времени, т.е. знать зависимости:
; 
; 
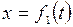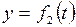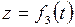. (7.2)
Уравнения (7.2) представляют собой уравнения движения точки в декартовых координатах.
В случае плоского движения, например, точка движется в плоскости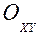 
, ее уравнения движения задаются в виде:
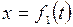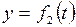, (7.3)
Рис. 7.2.
Уравнения (7.2), (7.3) представляют одновременно уравнения траектории точки в параметрической форме, где роль параметра играет величина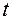 
. Исключив параметр 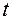, можно найти уравнение траектории в обычной форме, т.е. в виде, дающем зависимость между ее координатами:
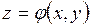– для пространственного движения;
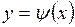– для плоского движения.
Векторный способ задания движения
Пусть точка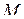 
движется по отношению к некоторой системе отсчета 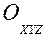. Положение этой точки можно определить, задав вектор 
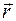, проведенный из начала координат 
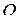в точку 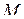. Вектор 
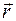называется радиусом – вектором точки 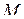. При движении точки 
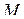вектор 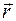будет с течением времени изменяться и по модулю и по направлению. Следовательно, 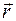можно задать вектором-функцией, зависящим от аргумента :
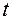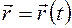(7.4.)
Геометрическое место концов вектора 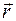, т.е. годограф этого вектора, определяет траекторию движущейся точки. Проектируя уравнение (7.4.) на оси координат получим:
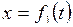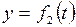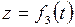; ; . (7.5).
Пример 1.
Заданы уравнения движения точки в координатной форме:
; 
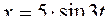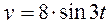(плоское движение). Значения 
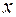и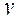 
в сантиметрах. Определить траекторию движения точки.
Решение.
Для определения траектории движения точки, необходимо исключить параметр 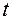из уравнений движения, заданных в координатной форме. Для этого возведем в квадрат данные уравнения:
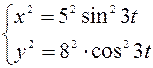, отсюда: 
.
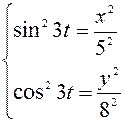Сложим соответственно левые и правые части полученных уравнений:
,
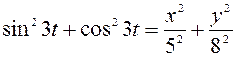Отсюда следует: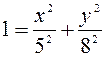 
, так как 
.
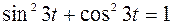Это есть каноническое уравнение эллипса с полуосями 5 и 8 см. Таким образом, данная точка совершает движение по эллипсу (рис.7.3.)
Рис. 7.3.
Ответ: траектория движения точки – эллипс.
Пример 2.
Уравнения движения точки на плоскости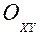 
задано:
, 
.
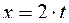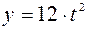Определить траекторию движения точки.
Решение.
Исключим параметр 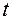из уравнений. Для этого из первого уравнения определим, что 
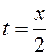и подставим во второе уравнение:
.
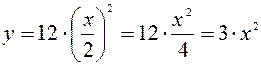Таким образом, получим: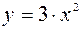 
.
Графиком траектории движения точки является парабола (рис. 7.4.).
Рис. 7.4
Ответ: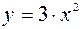 
– уравнение движения точки.
Пример 3.
Задано уравнение движения точки в векторной форме:
.
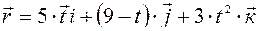Составить уравнение движения точки в координатной форме.
Решение.
Вследствие того, что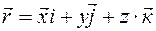 
, то отсюда следует:
; 
; 
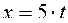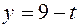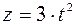
Ответ: уравнение движения точки: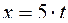 
; ; .
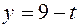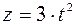Вопросы для самоконтроля
1. Что изучает кинематика?
2. Способы задания движения точки?
Задачи, рекомендуемые для самостоятельного решения: 10.1 – 10.23 [2].
Литература: [1], [3], [4].
Лекция 8
Вектор скорости точки
Скоростью называется векторная величина, модуль которой определяется изменением пройденного пути за единицу времени. Скорость будем обозначать символом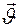 
, а ее модуль – 
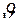, тогда:
; 
.
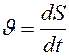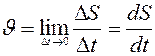Рис.8.1.
Так как скорость – вектор, то кроме модуля скорость имеет точку приложения и направление. Направление вектора скорости совпадает с направлением касательной к траектории движения точки в каждый момент времени.
Размерная скорость в СИ – м/с.
Вектор ускорения точки
Ускорением называется векторная величина, определяемая как изменение скорости в единицу времени.
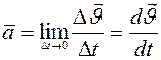(рис.8.2.)
Рис. 8.2
Размерность ускорения – м/с.
Определение скорости и ускорения точки при векторном способе задания движения (рис. 8.3)
Скорость точки определяется:
.
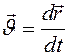Рис. 8.3
Ускорение точки определяется:
.
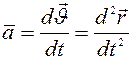Дата: 2019-02-25, просмотров: 256.
