Если данная система сил имеет равнодействующую, то момент этой равнодействующей относительно любой оси равен алгебраической сумме моментов слагаемых сил относительно той же оси: пусть Rx = å Fnx, тогда Mx(R) = åmx(Fn).
Пример 2. На горизонтальный вал лежащий в подшипниках А и В насажены перпендикулярно оси вала шкив радиусом r1 = 0.2м и барабан r2 = 0.15м. Вал приводится во вращение ремнем, накинутым на шкив; при этом равномерно поднимается груз массой m=180кг, привязанный к веревке, которая наматывается на барабан (рис. 5.6). Пренебрегая весом вала, барабана и шкива, определить реакции подшипников А и В и натяжение Т1 ведущей ветви ремня, если известно, что оно вдвое больше, чем Т2 ведомой ветви. Дано: a = 0.4м; b = 0.6м;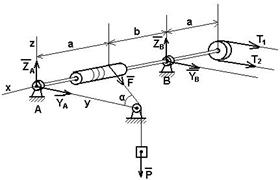 
a = 300.
Решение: по условию задачи, груз P равномерно поднимается, это значит, что вал вращается равномерно и поэтому все силы, действующие на него, находятся в равновесии. С учетом этого составим уравнения равновесия вала. В подшипниках действуют на вал силы реакции RAz, RAy, RBz, RBy.
Вычислим проекции всех сил на оси координат и их моменты относительно этих сил.
| Fn | F = P | T1 | T2 | RA | RB |
| Fny | F cosa | T1 | T2 | RAy | RBy |
| Fnz | - F sina | 0 | 0 | RAz | RBz |
| mx(Fn) | -F*r2 | T1*r1 | – T2*r1 | 0 | 0 |
| my(Fn) | F*b sina | 0 | 0 | 0 | - (a + b)RBz |
| mz(Fn) | F*b cosa | - T1*a | – T2*a | 0 | (a + b)RBy |
На ось Х проекции всех сил равны нулю
P cosa + T1 + T2 + RAy + RBY = 0 (1)
- P sina + RAz + RBz = 0 (2)
r2P + r1T1 – r1T2 = 0 (3)
b*P sina - (a + b)RBz = 0 (4)
b*P cosa - aT1 – aT2 + (a + b)RBy = 0 (5)
Решая эту систему уравнений, находим, что T1 =2.7 kH, T2 =1.35 kH,
RAz = 0.36 kH, RAy = -6.3 kH, RBz, = 0.54 kH, RBy. = 0.69 kH.
Ответ: T1 =2.7 kH, T2 =1.35 kH, RAz = 0.36 kH, RAy = -6.3 kH, RBz = 0.54 kH,
RBy = 0.69 kH.
Вопросы для самоконтроля
1. Как определяется момент силы относительно оси?
2. Уравнения равновесия твердого тела под действием пространственной системы сил?
3. Приведение пространственной системы сил к заданному центру?
Задачи, рекомендуемые для самостоятельного решения: 6.1 – 6.21, 7.1 – 7.12, 8.1 – 8.44 [2].
Література: [1], [3], [4].
Лекция 6.
Трение. Центр тяжести твердого тела.
Законы трения скольжения
Причиной трения является, прежде всего, шероховатость поверхностей и наличие молекулярных сил сцепления прижатых друг к другу тел.
1. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения, величина которой может принимать любые значения от 0 до значений Fпр, называемой предельной силой трения. Сила трения направлена в сторону, противоположную той, куда действующие силы стремятся сдвинуть тело.
2. Величина предельной силы равна произведению статического коэффициента трения на нормальное давление или нормальную реакцию:
Fпр = ¦0N.
3. Величина предельной силы трения не зависит от размеров соприкасающихся при трении поверхностей. При равновесии сила трения покоя: F £ ¦0N.
При движении сила трения направлена в сторону, противоположную движению, и равна произведению динамического коэффициента трения на нормальное давление: F = ¦N.
Значение динамического коэффициента ¦ зависит не только от материала и от состояния поверхности, но и от скорости движения.
Дата: 2019-02-25, просмотров: 271.
