Рассмотрим точку М, положение которой в сечении S определяется рассмотрением 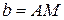 от полюса А и углом  (рис. 10.4). Если движение тела задано уравнениями (10.1), то координаты х и у точки М в осях О_ху будут:

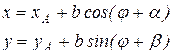,                                  (10.2)

где х_А, у_А и φ – известные по уравнениям (10.1) функции времени t. Уравнения (10.2), определяющие закон движения точки М в плоскости О_ху, дают одновременно уравнение траектории этой точки в параметрической форме. Уравнение траектории получается, исключив из системы (10.2) параметр t.

    Пример 1.

    Для кривошипно-шатунного механизма (рис. 10.4) определить уравнения плоского движения шатуна АВ. Угол поворота кривошипа изменяется согласно закону 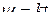, где k – постоянный коэффициент. Длина кривошипа ОА = r, шатуна АВ = l.

Решение

Рис. 10.4.

    Выбираем неподвижную систему координат с началом в точке О. Подвижную систему координат берем с началом в точке А, принадлежащей и кривошипу и шатуну.

    Ось х₁ проводим по шатуну АВ, ось у₁ – перпендикулярно к нему. Пусть точка А будет полюсом, тогда уравнения движения полюса имеет вид:

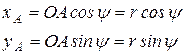
    Для нахождения третьего уравнения движения зависимости угла поворота шатуна от времени, спроектируем отрезок АВ на ось у. Обозначая через φ угол между осями х₁ и х₂, находим:

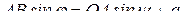, отсюда

.

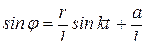Определение скоростей точек тела

    Плоскопараллельное движение твердого тела слагается из поступательного движения, при котором все точки тела движутся со скоростью полюса V_A, и из вращательного движения вокруг этого полюса.

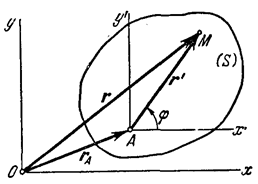
Рис. 10.4.

    Положение любой точки М, лежащей в сечении (S) тела определяется соотношением: 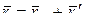, где 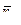 – радиус-вектор полюса;  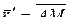– вектор, определяющий положение точки М относительно осей Ах΄у΄, перемещающихся вместе с полюсом А поступательно. Тогда

.

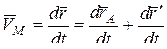    В полученном равенстве величина 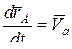 есть скорость полюса А; величина  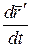равна скорости 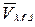, которую точка М получает при 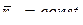, т.е. относительно осей Ах΄у΄ или, иначе говоря, при вращении тела вокруг полюса А. Таким образом, из предыдущего равенства следует, что

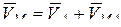.                                             (10.2)

При этом скорость 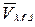 точки М во вращательном движении вокруг полюса А будет:

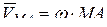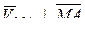, ( ),                                   (10.3)

где: 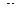 – угловая скорость вращения тела.

    Таким образом, скорость любой точки М тела геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости точки М в ее вращении вместе с телом вокруг этого полюса.

    Модуль и направление скорости 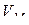 находятся построением соответствующего параллелограмма (рис. 10.5).

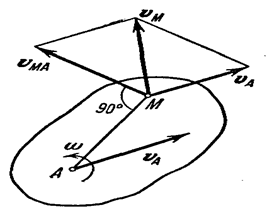
Рис. 10.5

Теорема о проекциях скоростей двух точек тела

    Теорема. Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны друг другу (рис. 10.6):

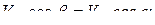
Рис. 10.6